Fibonacci-sekvens
Fibonacci-sekvensen är serien av siffror:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
nästa nummer hittas genom att lägga till de två siffrorna före det:
- 2 hittas genom att lägga till de två siffrorna före det (1+1),
- 3 hittas genom att lägga till de två siffrorna före det (1+2),
- 5 är (2+3),
- och så vidare!
exempel: nästa nummer i sekvensen ovan är 21+34 = 55
det är så enkelt!
Här är en längre lista:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
kan du räkna ut de närmaste siffrorna?
gör en Spiral
När vi gör rutor med dessa bredder får vi en fin spiral:
ser du hur rutorna passar snyggt ihop?
till exempel 5 och 8 gör 13, 8 och 13 Gör 21, och så vidare.

denna spiral finns i naturen!
se: Natur, det gyllene förhållandet och Fibonacci
regeln
Fibonacci-sekvensen kan skrivas som en ”regel” (se sekvenser och serier).
först numreras termerna från 0 och framåt så här:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
så termen nummer 6 kallas x6 (vilket motsvarar 8).
|
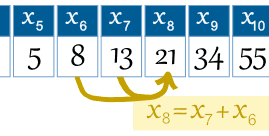
exempel: den 8: e termen är x8 = x7 + x6 |
 |
Så vi kan skriva regeln:
regeln är xn = xn−1 + xn−2
var:
- xn är termnummer ”n”
- xn−1 är föregående term (n−1)
- xn−2 är termen före det (n−2)
exempel: term 9 beräknas så här:
gyllene förhållande
och här är en överraskning. När vi tar några två på varandra följande (en efter den andra) Fibonacci-nummer, är deras förhållande mycket nära det gyllene förhållandet ”Kubi” som är ungefär 1.618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
vi behöver inte börja med 2 och 3, här valde jag slumpmässigt 192 och 16 (och fick sekvensen 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
det tar längre tid att få bra värden, men det visar att inte bara Fibonacci-sekvensen kan göra detta!
använda det gyllene förhållandet för att beräkna Fibonacci-nummer
och ännu mer överraskande är att vi kan beräkna vilket Fibonacci-nummer som helst med hjälp av det gyllene förhållandet:
xn = acign − (1−ci)n 5 ci
svaret kommer ut som ett heltal, exakt lika med tillägget av de föregående två termerna.
exempel: x6
x6 = (1.618034…)6 − (1−1.618034…) 6 5 6 5 x
när jag använde en kalkylator på detta (bara in i det gyllene förhållandet till 6 decimaler) fick jag svaret 8.00000033 , en mer exakt beräkning skulle vara närmare 8.
försök n=12 och se vad du får.
Du kan också beräkna ett Fibonacci-nummer genom att multiplicera det tidigare Fibonacci-numret med det gyllene förhållandet och sedan avrunda (fungerar för siffror över 1):
exempel: 8 KG = 8 kg 1,618034… = 12.94427… = 13 (avrundad)
några intressanta saker
Här är Fibonacci-sekvensen igen:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
det finns ett intressant mönster:
- titta på numret x3 = 2. Varje 3: e nummer är en multipel av 2 (2, 8, 34, 144, 610, …)
- titta på numret x4 = 3. Varje 4: e nummer är en multipel av 3 (3, 21, 144, …)
- titta på numret x5 = 5. Varje 5: e nummer är en multipel av 5 (5, 55, 610,…)
och så vidare (varje N: E nummer är en multipel av xn).
1/89 = 0,011235955056179775…
Lägg märke till de första siffrorna (0,1,1,2,3,5) är Fibonacci-sekvensen?
på ett sätt som de alla är, utom flera siffror (13, 21, etc) överlappar varandra, så här:
… osv …
0,011235955056179775… = 1/89
termer under noll
sekvensen fungerar under noll också, så här:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(bevisa för dig själv att varje nummer hittas genom att lägga till de två siffrorna före det!)
i själva verket har sekvensen under noll samma tal som sekvensen över noll, förutom att de följer a +-+- … mönster. Det kan skrivas så här:
x−n = (-1)n + 1 xn
som säger att termen” – n ”är lika med (-1)n+1 gånger termen ”n”, och värdet (-1)n+1 snyggt gör rätt +1, -1, +1, -1, … mönster.
historia
Fibonacci var inte den första som fick veta om sekvensen, den var känd i Indien hundratals år tidigare!

om Fibonacci mannen
hans riktiga namn var Leonardo Pisano Bogollo, och han bodde mellan 1170 och 1250 i Italien.
”Fibonacci” var hans smeknamn, vilket ungefär betyder ”son till Bonacci”.förutom att vara känd för Fibonacci-sekvensen hjälpte han till att sprida Hinduiska-arabiska siffror (som våra nuvarande siffror 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) genom Europa i stället för romerska siffror (I, II, III, IV, V, etc). Det har sparat oss alla en massa problem! Tack Leonardo.

Fibonacci Day
Fibonacci Day är den 23 November, eftersom den har siffrorna” 1, 1, 2, 3 ” som är en del av sekvensen. Så nästa Nov 23 låt alla veta!


Leave a Reply