Articles

enkla permutationer och kombinationer

by admin

Jag har alltid förvirrat ”permutation” och ”kombination” — vilken är vilken?

Här är ett enkelt sätt att komma ihåg: permutation låter komplicerat, eller hur? Och det är det. Med permutationer är varje liten detalj viktig. Alice, Bob och Charlie skiljer sig från Charlie, Bob och Alice (sätt in dina vänners namn här).

kombinationer, å andra sidan, är ganska lättsam. Detaljerna spelar ingen roll. Alice, Bob och Charlie är samma som Charlie, Bob och Alice.

permutationer är för listor (orderfrågor) och kombinationer är för grupper (ordning spelar ingen roll).

Du vet, ett” kombinationslås ”borde verkligen kallas ett”permutationslås”. Ordningen du lägger siffrorna i frågor.

enkla permutationer och kombinationer

ett sant” kombinationslås ” skulle acceptera både 10-17-23 och 23-17-10 som korrekt.

permutationer: de håriga detaljerna

låt oss börja med permutationer eller alla möjliga sätt att göra något. Vi använder fancy-pants termen” permutation”, så vi kommer att bry sig om varje sista detalj, inklusive ordningen på varje objekt. Låt oss säga att vi har 8 personer:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

hur många sätt kan vi tilldela ett 1: a, 2: a och 3: e platspris bland åtta tävlande? (Guld / Silver / brons)

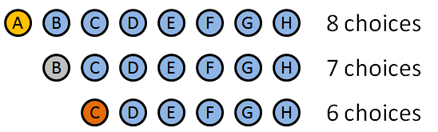
permuation exempel medaljer

Vi kommer att använda permutationer eftersom den ordning vi delar ut dessa medaljer frågor. Så här bryts det ner:

  • guldmedalj: 8 Val: A B C D E F G H (smart hur jag fick namnen att matcha med bokstäver, va?). Låt oss säga att A vinner guldet.
  • silvermedalj: 7 val: B C D E F G H. låt oss säga att B vinner silver.
  • bronsmedalj: 6 val: C D E F G H. låt oss säga … C vinner bronsen.

Vi valde vissa människor för att vinna, men detaljerna spelar ingen roll: vi hade 8 val först, sedan 7, sedan 6. Det totala antalet optioner var $8 * 7 * 6 = 336$.

låt oss titta på detaljerna. Vi var tvungna att beställa 3 personer av 8. För att göra detta började vi med alla alternativ (8) och tog dem sedan bort en i taget (7, sedan 6) tills vi fick slut på medaljer.

vi vet att faktoriell är:

\displaystyle{ 8! = 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 }

Tyvärr gör det för mycket! Vi vill bara ha $8 * 7 * 6$. Hur kan vi” stoppa ” faktorialen vid 5?

det är här permutationer blir coola: Lägg märke till hur vi vill bli av med $5 * 4 * 3 * 2 * 1$. Vad är ett annat namn för detta? 5 factorial!

Så, om vi gör 8!/5! vi får:

\displaystyle{\frac{8!}{5!} = \ frac{8 \cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1}{5 \cdot 4 \ cdot 3 \ cdot 2 \ cdot 1} = 8 \cdot 7 \cdot 6}

och varför använde vi numret 5? Eftersom det var kvar efter att vi plockade 3 medaljer från 8. Så ett bättre sätt att skriva detta skulle vara:

\displaystyle{\frac{8!}{(8-3)!}}

var 8!/(8-3)! är bara ett fint sätt att säga ” använd de första 3 siffrorna på 8!”. Om vi har n-objekt totalt och vill välja k i en viss ordning får vi:

\displaystyle{\frac{n!} {(n-k)!}}

och det här är den fina permutationsformeln: du har n-objekt och vill hitta antalet sätt k-objekt kan beställas:

\displaystyle{P(n,k) = \frac{n!} {(n-k)!}}

kombinationer, Ho!

kombinationer är lätta att gå. Ordning spelar ingen roll. Du kan blanda upp det och det ser likadant ut. Låt oss säga att jag är en cheapskate och har inte råd med separata Guld -, Silver-och bronsmedaljer. Faktum är att jag bara har råd med tomma burkar.

hur många sätt kan jag ge 3 burkar till 8 personer?

Tja, i det här fallet, den ordning vi väljer människor spelar ingen roll. Om jag ger en burk till Alice, Bob och sedan Charlie, är det samma som att ge till Charlie, Alice och sedan Bob. Hur som helst är de lika besvikna.

detta väcker en intressant punkt-vi har några uppsägningar här. Alice Bob Charlie = Charlie Bob Alice. För ett ögonblick, låt oss bara ta reda på hur många sätt vi kan ordna om 3 personer.

Tja, vi har 3 val för den första personen, 2 för den andra och bara 1 för den sista. Så vi har $3 * 2 * 1$ Sätt att omorganisera 3 personer.

vänta en minut … det här ser lite ut som en permutation! Du lurade mig!

det gjorde jag verkligen. Om du har n människor och du vill veta hur många arrangemang det finns för dem alla, det är bara n factorial eller N!

Så, om vi har 3 burkar att ge bort, finns det 3! eller 6 variationer för varje val vi väljer. Om vi vill ta reda på hur många kombinationer vi har skapar vi bara alla permutationer och delar med alla uppsägningar. I vårt fall får vi 336 permutationer (ovanifrån), och vi delar med 6 uppsägningar för varje permutation och får 336/6 = 56.

den allmänna formeln är

\displaystyle{C(n,k) = \frac{P(n,k)}{k!}}

vilket betyder ” hitta alla sätt att välja k-personer från n och dela med k! variant”. När vi skriver ut detta får vi vår kombinationsformel eller antalet sätt att kombinera k-objekt från en uppsättning n:

\displaystyle{C(n,k) = \frac{n!} {(n-k)!k!}}

ibland skrivs C(n,k) som:

\displaystyle{\binom {n}{k}}

vilket är binomialkoefficienten.

några exempel

Här är några exempel på kombinationer (ordning spelar ingen roll) från permutationer (orderfrågor).

  • kombination: välja ett team på 3 personer från en grupp på 10. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    Permutation: plocka en President, VP och Waterboy från en grupp av 10. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • kombination: välja 3 desserter från en meny med 10. C (10,3) = 120.

    Permutation: Lista dina 3 favorit desserter, i ordning, från en meny med 10. P (10,3) = 720.

memorera inte formlerna, förstå varför de fungerar. Kombinationer låter enklare än permutationer, och de är. Du har färre kombinationer än permutationer.

andra inlägg i denna serie

  1. enkla permutationer och kombinationer
  2. navigera i ett rutnät med kombinationer och permutationer
  3. hur man förstår kombinationer med multiplikation
  4. Varför multiplicerar vi kombinationer?