med box office-framgången för filmen ”Interstellar” är många människor glada över utsikterna till maskhål som ett medel för interstellär transport. Även om det för närvarande inte finns några bevis för att sådana exotiska föremål finns i naturen, är det möjligt att de kan skapas konstgjort, kanske från versioner av högre dimensionell strängteori och teknik av det grundläggande rymdtidskummet. Wormhole research är idag ett spännande ämne med dussintals artiklar publicerade i peer-reviewed tidskrifter varje år, men det är värt att påminnas om dess ursprung — och det börjar från en överraskande plats.1915 publicerade Albert Einstein sin allmänna relativitetsteori, sin beskrivning av tyngdkraften som snyggt definierar hur objekt kommer att locka varandra och påverka rymden och tiden runt dem. Många år senare skulle den amerikanska fysikern John Wheeler mynta frasen”space tells matter how to move, och matter tells space how to curve”. Einstein beskrev gravitationen som en manifestation av rymdtidskurvatur. Allmän relativitet är en kontinuerlig fältteori i motsats till partikelteorin om materia som ledde till kvantmekanik.Einstein var också involverad i utvecklingen av kvantmekanik, teorin som beskriver subatomära partiklar. Men han var inte helt nöjd med sin inneboende osäkerhet och probabilistiska karaktär. Så 1935 arbetade han med Nathan Rosen för att producera en fältteori för elektroner med allmän relativitet. Deras papper fick titeln”Partikelproblemet i den allmänna relativitetsteorin”. Einstein och Rosen undersökte möjligheten till en atomistisk teori om Materia och elektricitet som, exklusive diskontinuiteter (singulariteter) i fältet, använde inga andra variabler än beskrivningen (metrisk) av allmän relativitet och Maxwells elektromagnetiska teori. En av konsekvenserna var att den mest elementära laddade partikeln befanns vara en av nollmassa.

i slutändan var det som de producerade något ganska originellt. De började med ekvationerna för en sfäriskt symmetrisk massfördelning, som redan används för svarta hål, och känd som Schwarzschild-lösningen,

$$ds^2 = -\dfrac{1}{1 – 2m/r}dr^2-r^2(d\theta^2+\sin^2\theta d\phi^2) + (1-2m/r)dt^2$$

där \(ds^2\) är metriken och \(m=GM/C^2\) med sfäriska koordinater \((r,\Theta,\Phi)\) och tid \(t\).

de utförde en koordinattransformation för att ta bort regionen som innehåller krökningens singularitet, en diskontinuitet i rymdkurvatur som antyds av svarta hål och liknande fenomen. Singulariteten vid \(r=2M\) avlägsnades genom koordinattransformationen \(u^2 = R – 2M\), vilket resulterade i en slutlig lösning,

$$ds^2 = -4(u^2 + 2m)du^2 – (u^2 + 2M)^2 d\Omega^2 + \dfrac{u^2}{u^2 + 2M} dt^2$$

där \(D\Omega^2 = D\theta^2 + \Sin^2\theta d\PHI^2\).

denna lösning var en matematisk representation av fysiskt utrymme med ett utrymme av två asymptotiskt plana ark förbundna med en bro eller ett Schwarzschild maskhål med en ’hals’. Detta förbinder de två arken och analogt två separata delar av det verkliga, tredimensionella universum. Figur 1 visar utrymmet runt maskhålet, med utrymmet ovanför och under blir platt vid ”kanterna” när du zoomar ut till oändligheten.

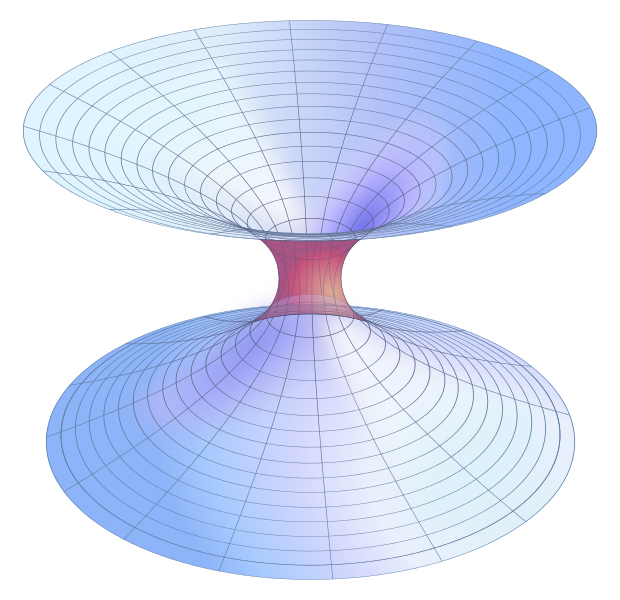
Nu var detta inte ett korsbart maskhål, för det var vi tvungna att vänta på ankomsten av fysiker John Wheeler på 1950-talet och Kip Thorne på 1980-talet. 1987, med uppmuntran av Carl Sagan för sin roman ”kontakt” (senare en långfilm), kunde Thorne och hans kollega Michael Morris konstruera en matematisk beskrivning, en metrisk, för att beskriva ett sfäriskt symmetriskt och statiskt maskhål med en verklig, ändlig omkrets. Detta hade en koordinatminskning från negativ oändlighet i minimalt krökt utrymme — till ett minimivärde där halsen var belägen och sedan ökade från halsen till positiv oändlighet-i ett annat minimalt krökt utrymme. Denna lösning har den utmärkande egenskapen att inte ha någon händelsehorisont-till skillnad från ett svart hål. Thorne och Morris papper fick titeln”maskhål i rymdtid och deras användning för interstellära resor: ett verktyg för undervisning i allmän relativitet”. Denna uppsats hjälpte till att etablera maskhålsforskning som nytt område för akademisk undersökning.

sedan dess har många papper publicerats, och astronomiska undersökningar har faktiskt genomförts och undersökt de längsta stjärnorna och galaxerna på jakt efter naturliga maskhål. Ingen har identifierats ännu, men kom ihåg ursprunget till detta forskningsområde — Einstein-Rosenbron var inte ett korsbart maskhål, och det var inte författarens avsikt att producera en, men de producerade den första matematiska beskrivningen av ett maskhål. De bör komma ihåg för detta. Vetenskaplig forskning producerar ofta något ganska oväntat med konsekvenser som når långt bortom forskarnas ursprungliga avsikter.

Kelvin F. Lång

sedan denna artikel publicerades har vår tidskrift Principium publicerat två nummer (nummer 9 & 10) där vi diskuterar maskhål och Einstein-Rosenbron mer detaljerat. Dessa frågor beskriver också en dags symposium om” interstellära maskhål: fysik och praktisk förverkligande ” organiserat av initiativet för interstellära studier i samarbete med British Interplanetary Society.