Definite Integrals
Du kanske vill läsa introduktion till Integration först!
Integration
|
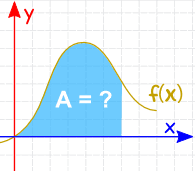
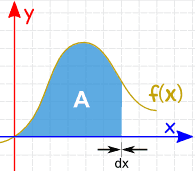
Integration kan användas för att hitta områden, volymer, centrala punkter och många användbara saker. Men det används ofta för att hitta området under grafen för en funktion som denna: |
 |
|
området kan hittas genom att lägga till skivor som närmar sig noll i bredd: och det finns regler för Integration som hjälper oss att få svaret. |
Notation
symbolen för ”Integral” är en snygg ”s” (för ”summa”, tanken på att summera skivor):
efter integralsymbolen sätter vi funktionen vi vill hitta integralen av (kallad integrand).
och avsluta sedan med dx för att betyda att skivorna går i X-riktningen (och närmar sig noll i bredd).
bestämd Integral
en bestämd Integral har start-och slutvärden: med andra ord finns det ett intervall .
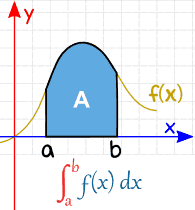
a och b (kallade gränser, gränser eller gränser) sätts längst ner och överst på ”S”, Så här:
 |
 |
|
| Definite Integral (from a to b) |
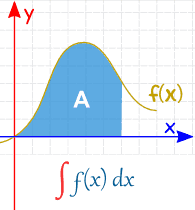
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
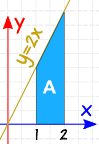
exempel: Vad är 2 2x 1 2x dx
vi blir ombedda för den bestämda integralen, från 1 till 2, av 2x dx
först måste vi hitta den obestämda integralen.
med hjälp av Integrationsreglerna finner vi att 2x DX = x2 + C
beräkna nu det vid 1 och 2:
- vid x=1: 2x DX = 12 + c
- vid x=2: 2x DX = 22 + C
subtrahera:
och ”C” avbryts … så med bestämda integraler kan vi ignorera C.
resultat:

kontrollera: med en så enkel form, låt oss också försöka beräkna området med geometri:
a = 2+42 × 1 = 3
Ja, det har ett område på 3.
(Yay!)
Notation: Vi kan visa den obestämda integralen (utan +C) inuti hakparenteser, med gränserna A och b efter, så här:
exempel (fortsättning)
ett bra sätt att visa ditt svar:
=
låt oss prova ett annat exempel:
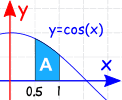
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
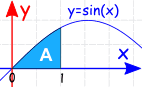
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
den obestämda integralen är:) + c
eftersom vi går från 0, kan vi bara beräkna integralen vid x = 1?
– cos (1) = -0,540…
vad? Är det negativt? Men det ser positivt ut i diagrammet.
Tja … vi gjorde ett misstag!
eftersom vi måste subtrahera integralet vid x=0. Vi borde inte anta att det är noll.
så låt oss göra det ordentligt, subtrahera en från den andra:
=
det är bättre!
men vi kan ha negativa regioner, när kurvan ligger under axeln:
exempel:
den bestämda integralen, från 1 till 3, av cos(x) dx:
Lägg märke till att en del av det är positivt och en del negativt.
Den bestämda integralen kommer att räkna ut nettovärdet.
låt oss göra beräkningarna:
=
hoppa det är mer negativt än positivt med nettoresultatet på -0.700….
så vi har denna viktiga sak att komma ihåg:
försök att integrera cos(x) med olika start-och slutvärden för att se själv hur positiva och negativa fungerar.
positivt område
men ibland vill vi att alla områden behandlas som positiva (utan att delen under axeln subtraheras).
i så fall måste vi beräkna områdena separat, som i det här exemplet:

exempel: Vad är det totala området mellan y = cos (x) och x-axeln, från x = 1 till x = 3?
det här är som det exempel vi just gjorde, men nu förväntar vi oss att allt område är positivt (föreställ oss att vi var tvungna att måla det).
så nu måste vi göra delarna separat:
- en för området ovanför x-axeln
- en för området under x-axeln
kurvan korsar x-axeln vid x = c/2 Så vi har:
från 1 till C/2:
= Sin(2) − sin(1)
från kub/2 till 3:
den sista kommer ut negativ, men vi vill att den ska vara positiv, så:
Total area = 0.159… + 0.859… = 1.018…
detta skiljer sig mycket från svaret i föregående exempel.
kontinuerlig
Åh ja, funktionen vi integrerar måste vara kontinuerlig mellan a och b: inga hål, hopp eller vertikala asymptoter (där funktionen går upp / ner mot oändligheten).
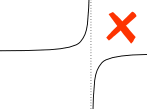
exempel:
en vertikal asymptot mellan A och b påverkar den bestämda integralen.
egenskaper
område ovanför − område under
integralet lägger till området ovanför axeln men subtraherar området nedan, för ett ”nettovärde”:
lägga till funktioner
integralen av f+g är lika med integralen av f plus integralen av g:
omvänd intervallet
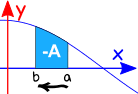
att vända intervallets riktning ger negativet av den ursprungliga riktningen.
![]()


Leave a Reply