matematik är mer ett maraton än en sprint — det är en lång, långsam och stadig slipning, med sällsynta ögonblick av genombrott. Ändå får vi då och då de uppskattade ”Eureka” – ögonblicken, de korta raderna med bokstäver och siffror som förändrar vetenskapen för alltid. Här är några av de mest kända ekvationerna, från de gamla grekerna till modern fysik.

Pythagoras sats (530 f. Kr.)

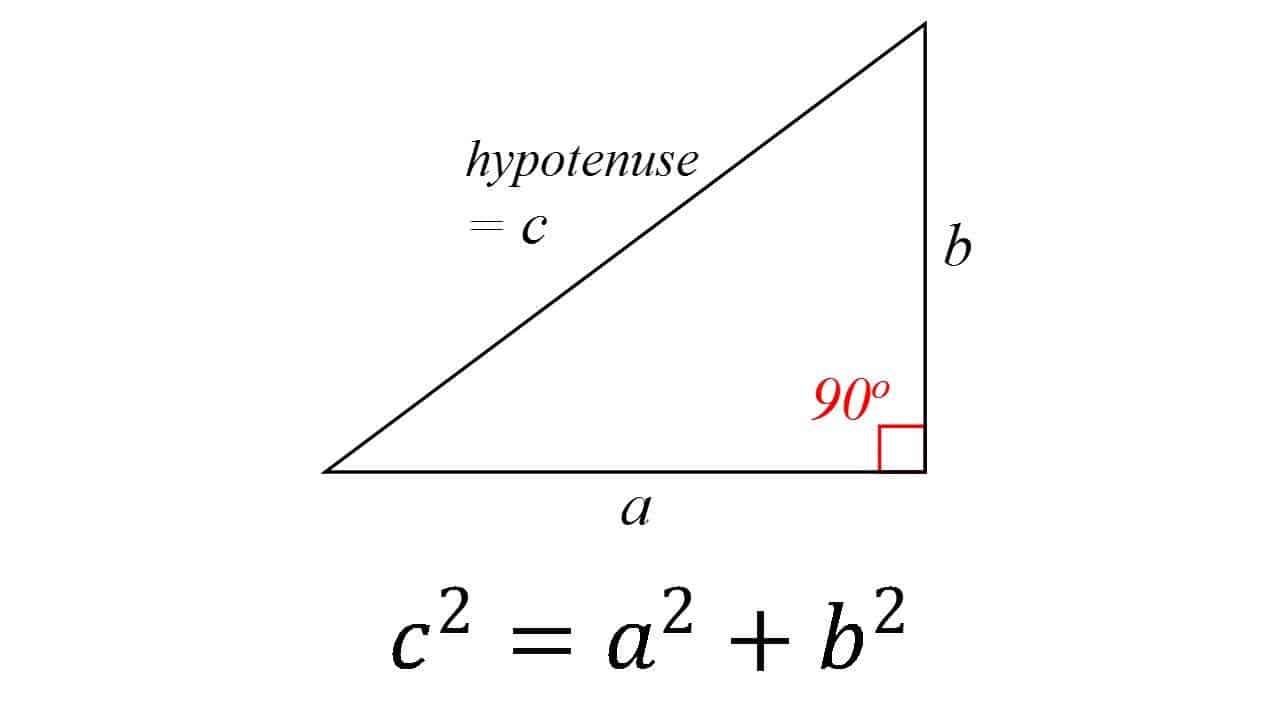
detta är ganska en av grundpelarna all geometri: i en rätt triangel är hypotenusens kvadrat (sidan motsatt rätt vinkel) lika med summan av kvadraterna för de andra två. Teorin tillskrivs i allmänhet den grekiska matematikern Pythagoras, även om det finns vissa bevis för att babyloniska matematiker förstod formeln. Det är också mycket möjligt att satsen var känd av många människor, men han var den första som bevisade det.

satsen har fått många bevis-kanske mest för någon matematisk sats. De är mycket olika, inklusive både geometriska bevis och algebraiska bevis, med några dejting tillbaka tusentals år.

komplexa tal

den italienska matematikern Gerolamo Cardano är den första kända som har infört komplexa nummer och kallar dem” fiktiva ” vid den tiden. Den matematiska utvecklingen av” i ” som det imaginära talet som representerar kvadratroten på -1 tillskrivs dock Leonhard Euler, en av de viktigaste matematikerna och forskarna i mänsklig historia.

komplexa tal är i grunden siffror som egentligen inte existerar, men som är mycket användbara för ett antal beräkningar. De består av siffror med en verklig del (de siffror vi alla vet) och en imaginär del (jag representerade här) och har praktiska tillämpningar inom många områden, inklusive fysik, kemi, biologi, ekonomi, elektroteknik och statistik.

logaritmerna

logaritmer är i grunden den inversa funktionen av exponentiering. Du behöver ett tal (N), en bas (A) och logaritmen för N I bas A kommer att vara x, där N är lika med A till kraften i x. det kan verka som bara ett annat sätt att skriva samma sak (och på sätt och vis är det), men logaritmer har en myriad av praktiska tillämpningar, används i psykologi, ekonomi och mätningar av många fysiska fenomen (som pH eller jordbävningsstorlek).logaritmer förespråkades offentligt av John Napier 1614, i en bok med titeln Mirifici Logarithmorum Canonis Descriptio (beskrivning av Logaritmernas underbara regel) — en passande titel. Ett speciellt fall av logaritm är den naturliga logaritmen-e, där e är ett irrationellt och transcendentalt tal ungefär lika med 2,71828182845. Faktum är att e själv har en fascinerande historia och ett imponerande antal applikationer, men det är en historia för en annan gång.

kalkyl

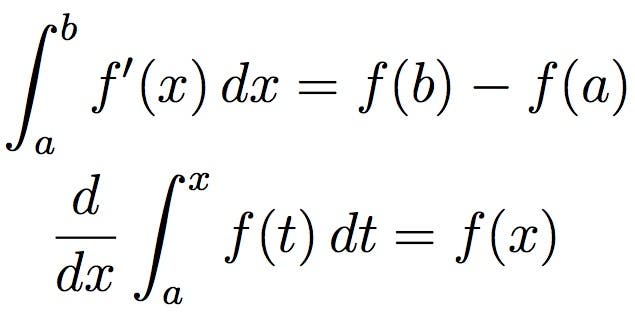
Få fält av matematik har varit lika effektiva som kalkyl. Utvecklad på 17-talet av Isaac Newton och Gottfried Wilhelm Leibniz, kalkyl används ofta inom vetenskap, teknik och ekonomi. Calculus fokuserar vanligtvis på att hantera små mängder, särskilt oändligt små mängder. Genom kalkyl kan dessa behandlas som reella tal, även om de är tekniskt oändligt små.

för en enklare visualisering kan integration, avbildad ovan, betraktas som mätning av området under en kurva, definierad av en funktion.

tyngdlagen

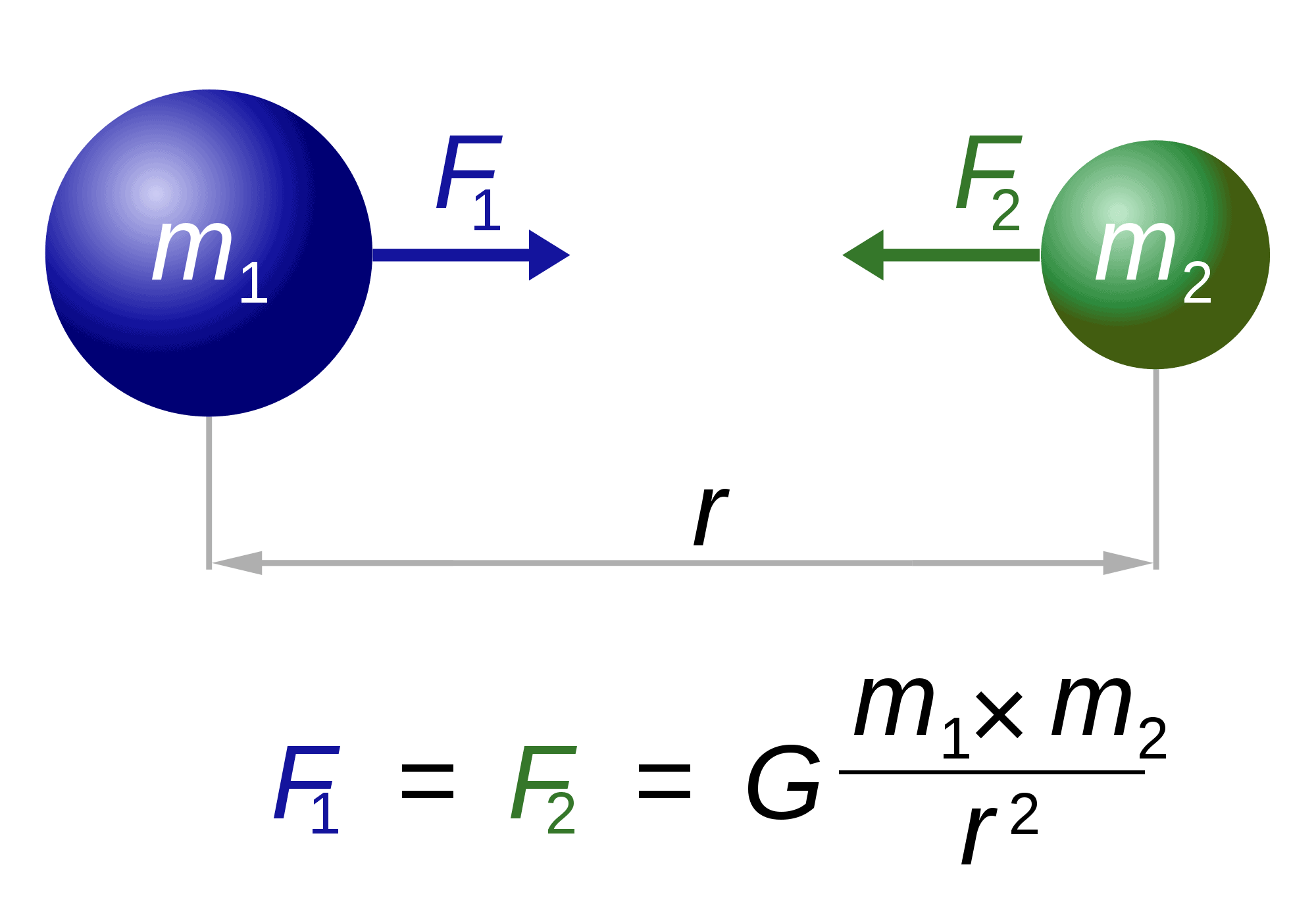
På tal om Newton är han också” ansvarig ” för en av världens mest kända och spektakulära ekvationer: tyngdlagen.

lagen beskriver i grunden hur två kroppar av massor m1 och m2 lockas till varandra. Kraften (F1, F2) är omvänt proportionell mot kvadraten av avståndet mellan dem (r). Den enda återstående faktorn, G, är en gravitationskonstant. Naturen hos denna konstant förblir svårfångad.

allmän relativitet

i nästan 200 år definierade Newtons lag vår nivå av förståelse för mekanik. Einsteins arbete på 20 — talet tog saker till nästa nivå-dessa två prestationer torn på de högsta piedestalerna i fysikens värld.

allmän relativitet är i huvudsak en geometrisk teori om gravitation, generalisering av Newtons teori som ger en enhetlig beskrivning av gravitationen som en geometrisk egenskap hos rum och tid — eller rymdtid. I synnerhet visade Einstein inte bara att det finns en sådan sak som ”rymdtid” som sammanfogar de tre dimensionerna med den 4: e dimensionen av tiden, men han visade också att denna rymdtid kan böjas av tyngdkraften, med krökningen direkt relaterad till energi och momentum av oavsett Materia och strålning är närvarande.

termodynamikens andra lag

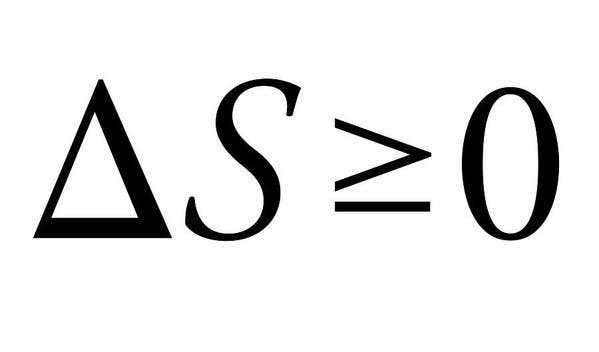
termodynamikens andra lag är varför vi inte kan ha trevliga saker i universum. Skämt åt sidan, termodynamikens fyra lagar definierar grundläggande fysiska kvantiteter (temperatur, energi och entropi) som kännetecknar termodynamiska system. Den andra, i synnerhet, sticker ut här på grund av dess enkelhet, men absolut massiva konsekvenser.

lagen säger i huvudsak att summan av entropierna hos de interagerande termodynamiska systemen alltid måste öka eller högst förbli konstant. När energi förändras från en form till en annan eller materia rör sig runt, ökar entropin (eller störningen) i ett slutet system. Alla skillnader i temperatur, tryck och densitet tenderar att platta ut efter ett tag

Maxwells ekvationer

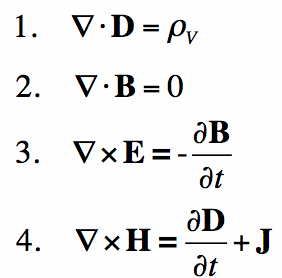
enkelt uttryckt är Maxwells ekvationer för elektromagnetism vad Newtons lag är för mekanik. De ger en matematisk grund för klassisk elektromagnetism, klassisk optik och elektriska kretsar. De används ofta i själva enheten du läser detta på-i princip alla elektroniska enheter.

Maxwells lagar beskriver hur elektriska och magnetiska fält genereras av laddningar, strömmar och förändringar av fälten. Ett betydande genombrott var demonstrationen att elektriska och magnetiska fält sprider sig vid ljusets hastighet.

Eulers identitet

slutligen är detta kanske den mest eleganta ekvationen, en sak av högsta skönhet, eftersom det involverar alla ”grundläggande” siffror:

• 0, vilket är neutralt för addition och subtraktion;
• 1, vilket är neutralt för multiplikation och division;
• e, som är neutral för addition och subtraktion;
• 1, vilket är neutralt för multiplikation och division;
• e, som är neutral för multiplikation och division;
• e, vilket är en är Eulers nummer (Se ovan), basen för naturliga logaritmer;
• I är den imaginära enheten (se ovan); och
• ozi är pi, förhållandet mellan omkretsen av en cirkel och dess diameter.

att hitta en relation som förenar alla dessa siffror är inget annat än hisnande och verkar ganska osannolikt. Demonstrationen är inte exakt enkel, men du kan se den här.

det är bara passande att Stanford University matematikprofessor Keith Devlin beskrev ekvationen och sa att”som en Shakespeare — Sonett som fångar kärlekens väsen, eller en målning som tar fram skönheten i den mänskliga formen som är mycket mer än bara hud djup, når Eulers ekvation ner i existensens djup”

det är inte ofta att matematik och fysik kokar ner till enkla och eleganta ekvationer-men när de gör det är det ganska en syn att se.