utvärdering av Cohens Kappa

värdet för kappa kan vara mindre än 0 (negativt). En poäng på 0 innebär att det finns slumpmässig överenskommelse mellan bedömare, medan en poäng på 1 innebär att det finns ett fullständigt avtal mellan bedömarna. Därför innebär en poäng som är mindre än 0 att det finns mindre överenskommelse än slumpmässig chans. Nedan kommer jag att visa dig formeln för att utarbeta detta, men det är viktigt att du bekantar dig med figur 4 för att ha en stark förståelse.

anledningen till att jag markerade två galler kommer att bli tydlig på ett ögonblick, men för nu, låt mig bryta ner varje rutnät.

A = > det totala antalet instanser som båda bedömarna sa var korrekta. Bedömarna är överens.

B = > det totala antalet instanser som Rater 2 sa var felaktigt, men Rater 1 sa var korrekta. Detta är en oenighet.

C = > det totala antalet instanser som Rater 1 sa var felaktigt, men Rater 2 sa var korrekta. Detta är också en oenighet.

D = > det totala antalet instanser som båda bedömarna sa var felaktiga. Bedömare är överens.

för att räkna ut kappa-värdet måste vi först veta sannolikheten för överenskommelse (detta förklarar varför jag lyfte fram avtalsdiagonalen). Denna formel härleds genom att lägga till antalet tester där bedömarna är överens och sedan dela den med det totala antalet tester. Med hjälp av exemplet från Figur 4 skulle det betyda (A + D)/(A + B+ C+ D).

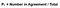
perfekt! Nästa steg är att räkna ut sannolikheten för slumpmässig överenskommelse. Använda figur 4 som en guide, det förväntade värdet är det totala antalet gånger som Rater 1 nämnda korrekta dividerat med det totala antalet instanser, multiplicerat med det totala antalet gånger som Rater 2 nämnda korrekta dividerat med det totala antalet instanser, läggas till det totala antalet gånger som Rater 1 nämnda felaktiga multiplicerat med det totala antalet gånger som Rater 2 nämnda felaktiga. Det är mycket information att ta in där så i Figur 6 har jag formulerat denna ekvation med hjälp av rutnätet ovan.

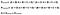
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

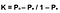
bra! Du kan nu skilja mellan tillförlitlighet och giltighet, förklara Cohens kappa och utvärdera den. Denna statistik är mycket användbar, men eftersom jag har förstått hur det fungerar tror jag nu att det kan vara underutnyttjat när man optimerar algoritmer till en specifik metrisk. Dessutom gör Cohens kappa också ett bra jobb med att mäta både flerklassiga och obalanserade klassproblem.

P. S. Om det är något som du vill att jag ska täcka att göra med datavetenskap, kan du direktmeddelande mig på Twitter @KurtisPykes eller lämna ett svar på det här inlägget.