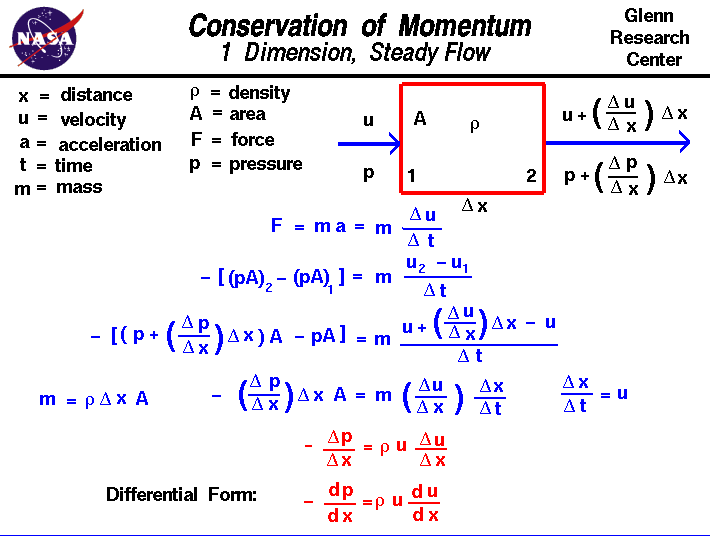
bevarande av momentum är ett grundläggande begrepp för fysisktillsammans medkonservering av energiochkonservering av massa.Momentum definieras som massan av ett objekt multiplicerat med objektets hastighetav objektet.Bevarandet av momentum säger att, inom någon problemdomän, mängden momentum förblir konstant;momentum skapas varken eller förstörs, men ändras baragenom krafternas handling som beskrivs av Newtons rörelselagar.Att hantera momentum är svårare än att hantera massa och energi eftersomögonblick är avektorkvantitethar både en storlek och en riktning. Momentum bevaras i alla trefysiska riktningar samtidigt. Det är ännu svårare när man hanterar agaseftersom krafter i en riktning kan påverka momentet i en annan riktningpå grund av kollisioner av många molekyler.På den här bilden presenterar vi ett mycket, mycket förenklat flödesproblem där egenskaper bara ändras i en riktning.Problemet förenklas ytterligare genom att överväga ett stadigt flöde som inte förändras med tiden och genom att begränsa krafterna till endast de som är associerade med thepressure.Be medveten om att verkliga flödesproblem är mycketmer komplexaän det här enkla exemplet.

låt oss överväga flödet av en gas genom en domän där flödesegenskaperändra bara i en riktning, som vi kommer att kalla ”x”. Gasen kommer in i domainat station 1 med viss hastighet u och lite tryck pand går ut vid station 2 med ett annat värde av hastighet och tryck. För enkelhetens skull antar vi attdensiteten r förblir konstant inom domänenoch att området A genom vilket gasen flyter också förblir konstant. Placeringen av stationerna 1 och 2 är separerademed ett avstånd som heter del x. (Delta är den lilla triangeln på glidenoch är den grekiska bokstaven ”d”. Matematiker använder ofta denna symbol för att betecknaen förändring eller variation av en kvantitet. Web print font stöder inteDe grekiska bokstäverna, så vi kommer bara kalla det ”del”.) En förändring med avstånd kallas en gradientatt undvika förvirring med en förändring med tiden som kallas en hastighet.Hastighetsgradienten indikeras av del u / del x; förändringen i hastighet perchange i avstånd. Så vid station 2 ges hastigheten av hastighetenvid 1 plus gradienten gånger avståndet.

ett liknande uttryck ger trycketvid utgången:

Newton ’ Sandra lagen om rörelse staterden kraften F är lika med förändringen i momentum medrespekt till tiden. För ett objekt med konstant massm detta minskar till Mass gånger acceleration a.An acceleration är en förändring i hastighet med en förändring i tid(del u / Del t). Sedan:

kraften i detta problemkommer från tryckgradienten. Eftersom trycket är en kraft per ytenhet, är nettokraften på vår flytande domän trycket gånger området vidutgång minus trycket gånger området vid ingången.

minustecknet vidbörjan av detta uttryck används eftersom gaser rör sig från en regionav högt tryck till ett område med lågt tryck; om trycket ökar MedX kommer hastigheten att minska. Ersätter våra uttryck för hastighetoch tryck:

förenkla:

notera att (del x / Del t) är thevelocity och att massan är densiteten r gånger volymen (area gånger del x):

förenkla:

del p / del x och del u / del xrepresenterar tryck-och hastighetsgradienterna.Om vi krymper vår domän ner till differentiella storlekar blir dessa gradienter skillnader:

detta är en endimensionell, stadig form aveulers Equation.It är intressant att notera att tryckfallenav en vätska (termen till vänster) är proportionell mot både värdet avvelocity och gradienten av hastigheten.En lösning av denna momentumekvation ger oss formen avdynamiskt trycksom visas ibernoullis ekvation.

aktiviteter:
guidade turer

• grundläggande Fluid Dynamics ekvationer:

navigering ..

Nybörjarguide hemsida