Beanz Magazine
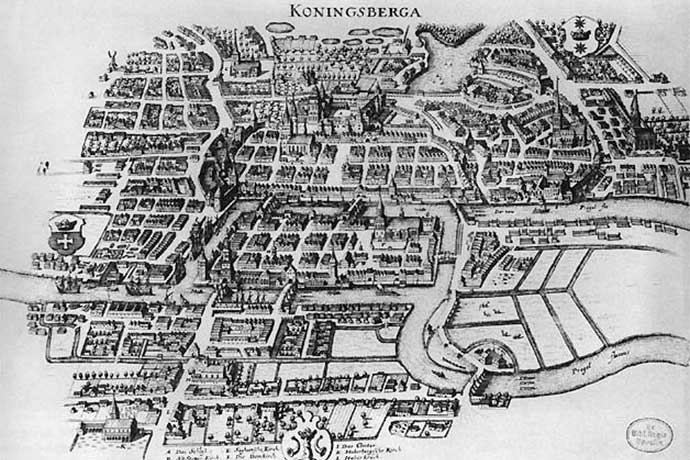
karta av Merian-Erben (1652) på Wikipedia
den här månadens matematiska pussel går tillbaka till 1735 när det först löstes av Leonhard Euler, en schweizisk matematiker och fysiker.
pusslet kallas de sju broarna i K Jacobnigsberg. Den är baserad på en verklig stad, sedan i Preussen, nu Kaliningrad i Ryssland. Staden delas av en flod med två öar däremellan och, längre nedströms, floden delar staden igen.
problemet är bedrägligt enkelt: det finns (eller var på Eulers tid) sju broar för att ansluta de två öarna och de nedströms delarna av staden. Euler undrade om en person kunde gå över var och en av de sju broarna en gång och bara en gång för att röra vid varje del av staden. Att starta och sluta på samma plats var inte ett krav.
Här är en karta som du kan använda för att försöka lösa problemet själv:
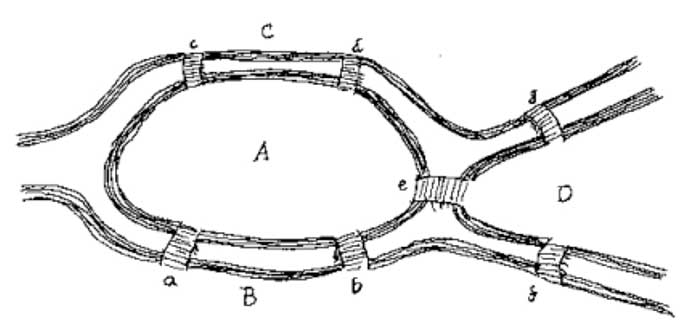
vilket tycker du är viktigare att lösa detta problem: antalet broar eller platsen för varje bro?
svar: antalet broar.
Euler visade att antalet broar måste vara ett jämnt antal, till exempel sex broar i stället för sju, om du vill gå över varje bro en gång och resa till varje del av K Jacobnigsberg. Lösningen ser varje bro som en slutpunkt, ett vertex i matematiska termer och anslutningarna mellan varje bro (vertex). Euler insåg bara ett jämnt antal broar gav rätt resultat av att kunna röra varje del av staden utan att korsa en bro två gånger.
Euler använde matematik för att bevisa att det var omöjligt att korsa alla sju broar bara en gång och besöka varje del av K. Genom att göra det satte han igång en serie upptäckter och insikter om hur rymden och korsande utrymmen kan definieras, liksom deras egenskaper. En detaljerad beskrivning av Eulers lösning i Wikipedia-länken under denna artikel.
Om du någonsin sett en mobius-remsa, har du till exempel sett ett exempel på topologi, ett matematiskt studieområde utvecklats från Eulers lösning på detta problem. Topologi handlar om rymden och hur saker förbinder varandra, liksom kontinuitet och gränser för rymden. Topologi studerar också hur egenskaperna hos ett utrymme förändras och inte förändras när utrymmet expanderas eller kontrakteras.
i databehandling är topologi användbar för att förstå nätverk (vägar) data kan flöda inom vilket system som helst, liksom hur uppsättningar data kan relatera till varandra. De sju broarna i K Kubnigsberg liknar också ett annat vanligt datorproblem som ibland kallas resande säljare Problem där du försöker hitta den mest effektiva vägen med tanke på en uppsättning begränsningar som de sju broarna i Eulers problem.
Icke-matematiker (sannolikt du, definitivt jag) upplever resande säljare problemet när vi får på ett tåg eller buss. Problemet med resande säljare är att räkna ut det mest effektiva sättet att resa mellan par städer med angivna avstånd. Att hantera knappa resurser (tåg, bussar) som reser längs ändliga rutter är ett perfekt problem för datorer att lösa eftersom datorer är snabbare och effektivare. Men först behöver vi Euler och andra för att ange problemet och definiera lösningar med matematik. Vi programmerar sedan våra datorer för att göra matten.
topologi behandlar också uppsättningsteori, hur grupper av saker kan sorteras i uppsättningar för att identifiera gemensamma element med andra grupper såväl som unika element. Ett Venn-diagram är ett bra exempel på en uppsättning. Och programmering måste ibland sortera data på olika sätt. Vilken sorteringsmetod som fungerar bäst för en situation kan bestämmas av uppsättningsteori.
och vad hände med de sju broarna från Eulers tid? Två överlevde inte andra världskriget. två broar revs och ersattes med en enda motorväg. Av de tre återstående broarna byggdes en om 1935 medan de andra två förblir intakta som Euler kände dem. Och, naturligtvis, K Kubnigsberg, Preussen har bytt namn till Kaliningrad, Ryssland.
Leave a Reply