Energetik av Jonbindningsbildning

jonbindningar bildas när positivt och negativt laddade joner hålls samman av elektrostatiska krafter. Tänk på ett enda par joner, en katjon och en anjon. Hur stark kommer kraften i deras attraktion att vara? Enligt Coulombs lag är energin hos den elektrostatiska attraktionen (\(E\)) mellan två laddade partiklar proportionell mot storleken på laddningarna och omvänt proportionell mot det internukleära avståndet mellan partiklarna (\(r\)):

\

\

där varje jonladdning representeras av symbolen Q. proportionalitetskonstanten k är lika med 2,31 10-28 J·M. detta värde på k inkluderar laddningen av en enda elektron (1,6022 10-19 C 10-19 C) för varje jon. Ekvationen kan också skrivas med laddningen av varje jon, uttryckt i coulombs (C), införlivad i konstanten. I detta fall är proportionalitetskonstanten, k, lika med 8,999 x 109 j·m/C2. I det givna exemplet Q1 = + 1 (1,6022 10-19 C) och Q2 = -1 (1,6022 10-19 C). Om Q1 och Q2 har motsatta tecken (som i NaCl, till exempel, där Q1 är +1 för Na+ och Q2 är -1 för Cl−), är E negativ, vilket innebär att energi frigörs när motsatt laddade joner samlas från ett oändligt avstånd för att bilda ett isolerat jonpar.

energi frigörs alltid när en bindning bildas och på motsvarande sätt kräver det alltid energi för att bryta en bindning.

som visas av den gröna kurvan i den nedre halvan av figur \(\PageIndex{1}\), skulle den maximala energin släppas när jonerna är oändligt nära varandra, vid r = 0. Eftersom joner upptar utrymme och har en struktur med den positiva kärnan omgiven av elektroner, kan de dock inte vara oändligt nära varandra. På mycket korta avstånd blir repulsiva elektron–elektroninteraktioner mellan elektroner på intilliggande joner starkare än de attraktiva interaktionerna mellan joner med motsatta laddningar, vilket visas av den röda kurvan i den övre halvan av figur \(\PageIndex{1}\). Systemets totala energi är en balans mellan de attraktiva och repulsiva interaktionerna. Den lila kurvan i Figur \(\PageIndex{1}\) visar att systemets totala energi når ett minimum vid r0, den punkt där de elektrostatiska repulsionerna och attraktionerna är exakt balanserade. Detta avstånd är detsamma som det experimentellt uppmätta bindningsavståndet.

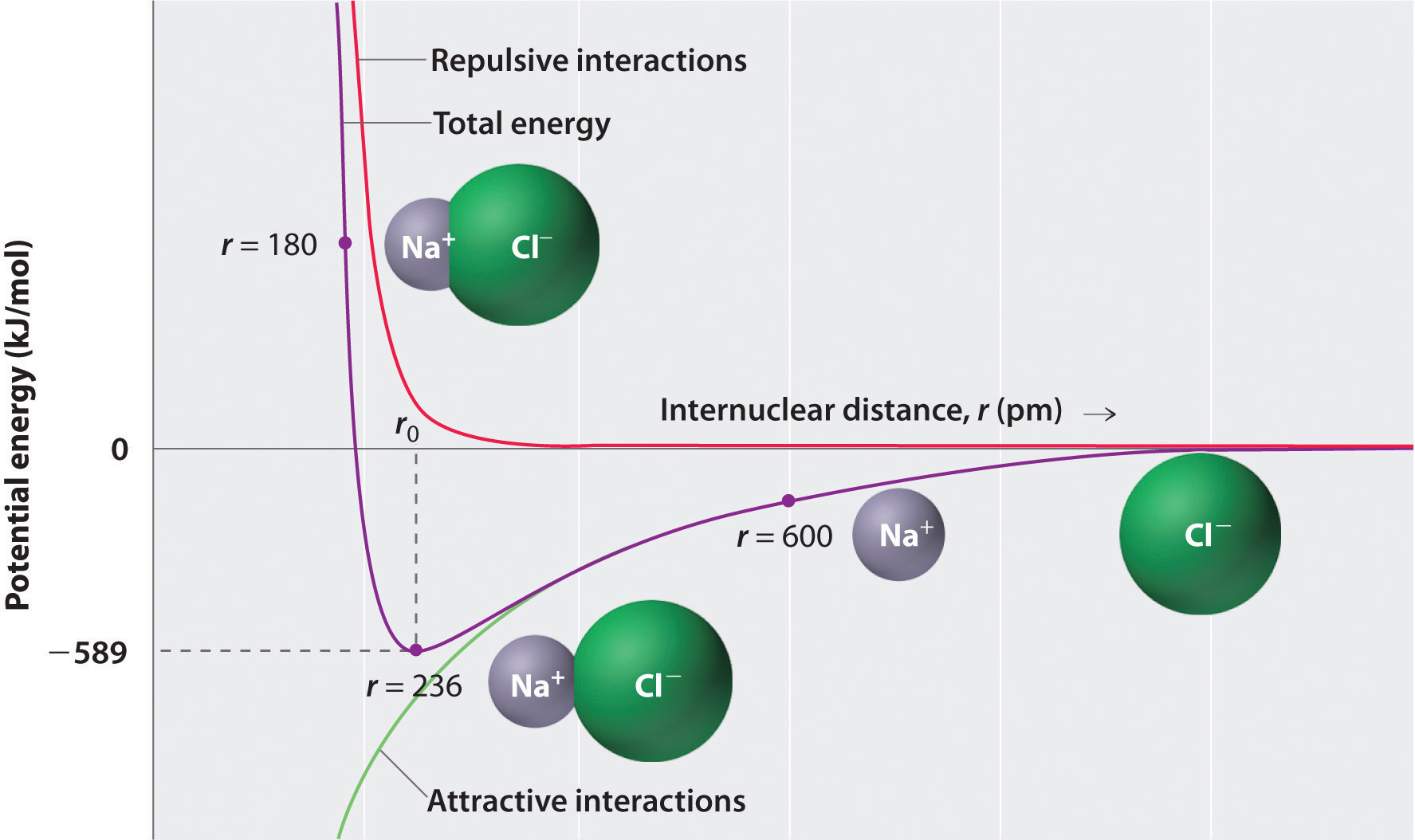
Tänk på den energi som frigörs när en gasformig \(Na^+\) Jon och en gasformig \(Cl^-\) Jon sammanfogas från r = Aci till r = r0. Med tanke på att det observerade gasfasinternukleära avståndet är 236 pm, är energiförändringen associerad med bildandet av ett jonpar från en \(Na^+_{(g)}\) Jon och en \(Cl^-_{(g)}\) Jon följande:

\ &= (2,31 \gånger {10^ {- 28}}\rm{J}\cdot \cancel{m} ) \vänster( \dfrac{( + 1)( – 1)}{236\; \Avbryt{pm} \ gånger 10^ {- 12} \Avbryt{m/pm}} \höger) \\ &= – 9.79 \ gånger 10^ {- 19}\; J/ion\; pair \label{Eq2} \end{align*}\]

det negativa värdet indikerar att energi frigörs. Vår konvention är att om en kemisk process ger energi till omvärlden är energiförändringen negativ. Om det kräver energi är energiförändringen positiv. För att beräkna energiförändringen i bildandet av en mol NaCl-par måste vi multiplicera energi per jonparet med Avogadros nummer:

\

detta är den energi som frigörs när 1 mol gasformiga jonpar bildas, inte när 1 mol positiva och negativa joner kondenserar för att bilda en kristallin gitter. På grund av långväga interaktioner i gitterstrukturen motsvarar denna energi inte direkt gitterenergin hos det kristallina fasta ämnet. Det stora negativa värdet indikerar emellertid att det är energiskt mycket gynnsamt att föra positiva och negativa joner tillsammans, oavsett om ett jonpar eller en kristallin gitter bildas.

Vi sammanfattar de viktiga punkterna om jonbindning:

• vid r0 är jonerna mer stabila (Har en lägre potentiell energi) än de är på ett oändligt internukleärt avstånd. När motsatt laddade joner sammanförs från r = kub till r = r0 sänks systemets energi (energi frigörs).
• på grund av den låga potentiella energin vid r0 måste energi läggas till systemet för att separera jonerna. Mängden energi som behövs är bindningsenergin.
• systemets energi når ett minimum vid ett visst internukleärt avstånd (bindningsavståndet).