Secvența Fibonacci
secvența Fibonacci este seria de numere:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
următorul număr se găsește prin adăugarea celor două numere înaintea Lui:
- 2 se găsește prin adăugarea celor două numere înaintea lui (1+1),
- 3 se găsește prin adăugarea celor două numere înaintea lui (1+2),
- 5 este (2+3),
- și așa mai departe!
exemplu: următorul număr din secvența de mai sus este 21+34 = 55
este atât de simplu!
Iată o listă mai lungă:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
puteți afla următoarele numere?
face o spirală
când facem pătrate cu aceste lățimi, obținem o spirală frumoasă:
vedeți cum pătratele se potrivesc perfect împreună?
De exemplu, 5 și 8 face 13, 8 și 13 face 21, și așa mai departe.

această spirală se găsește în natură!
vezi: Natura, raportul de aur și Fibonacci
regula
secvența Fibonacci poate fi scrisă ca o „regulă” (vezi secvențe și serii).
în primul rând, termenii sunt numerotați de la 0 începând astfel:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
deci termenul numărul 6 se numește x6 (care este egal cu 8).
|
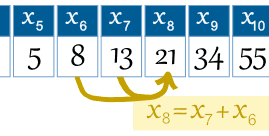
exemplu: al 8−lea termen este al 7−lea termen plus al 6-lea termen: x8 = x7 + x6 |
|
deci, putem scrie regula:
regula este xn = xn-1 + xn-2
unde:
- xn este termenul numărul „n”
- xn−1 este termenul anterior (n−1)
- xn−2 este termenul anterior (n−2)
exemplu: termenul 9 Se calculează astfel:
raportul de aur
și aici este o surpriză. Când luăm oricare două numere Fibonacci succesive (una după alta), raportul lor este foarte apropiat de raportul de aur „hectolixt”, care este de aproximativ 1.618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
nu trebuie să începem cu 2 și 3, Aici am ales aleatoriu 192 și 16 (și am obținut secvența 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
este nevoie de mai mult timp pentru a obține valori bune, dar arată că nu doar secvența Fibonacci poate face acest lucru!
folosind raportul de aur pentru a calcula numerele Fibonacci
și chiar mai surprinzător este faptul că putem calcula orice număr Fibonacci folosind raportul de aur:
xn = (1−) n (5) n (5)
răspunsul iese ca un număr întreg, exact egal cu adăugarea celor doi termeni anteriori.
exemplu: x6
x6 = (1.618034…)6 − (1−1.618034…) 6 5
când am folosit un calculator pe acest (introducând doar raportul de aur la 6 zecimale) am primit răspunsul 8.00000033 , un calcul mai precis ar fi mai aproape de 8.
încercați n=12 și vedeți ce obțineți.
de asemenea, puteți calcula un număr Fibonacci prin înmulțirea numărului Fibonacci anterior cu raportul auriu și apoi rotunjirea (funcționează pentru numere de mai sus 1):
exemplu: 8… = 12.94427… = 13 (rotunjite)
unele lucruri interesante
aici este secvența Fibonacci din nou:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
există un model interesant:
- Uită-te la numărul x3 = 2. Fiecare număr 3 este un multiplu de 2 (2, 8, 34, 144, 610, …)
- Uită-te la numărul x4 = 3. Fiecare număr 4 este un multiplu de 3 (3, 21, 144,…)
- Uită-te la numărul x5 = 5. Fiecare număr 5 este un multiplu de 5 (5 ,55, 610,…)
și așa mai departe (fiecare al n-lea număr este un multiplu de xn).
1/89 = 0, 011235955056179775…
observați că primele cifre (0,1,1,2,3,5) sunt secvența Fibonacci?
într-un fel, toate sunt, cu excepția numerelor de mai multe cifre (13, 21, etc) se suprapun, astfel:
… etc…
0.011235955056179775… =1/89
Termeni Sub Zero
secvența funcționează și sub zero, astfel:
| n= | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(dovediți-vă că fiecare număr este găsit adunând cele două numere dinaintea lui!)
de fapt, secvența Sub zero are aceleași numere ca și secvența peste zero, cu excepția faptului că urmează a +-+- … model. Poate fi scris astfel:
x−n = (-1)n + 1 xn
care spune că termenul „- n” este egal cu (-1)N+1 ori termenul „n” , iar valoarea (-1) n+1 face corect +1, -1, +1, -1, … model.
Istorie
Fibonacci nu a fost primul care a aflat despre secvență, era cunoscut în India cu sute de ani înainte!

despre Fibonacci omul
numele său real a fost Leonardo Pisano Bogollo, și a trăit între 1170 și 1250 în Italia.
„Fibonacci” a fost porecla lui, care înseamnă aproximativ „fiul lui Bonacci”.pe lângă faptul că a fost faimos pentru secvența Fibonacci, el a ajutat la răspândirea cifrelor hinduse-arabe (cum ar fi numerele noastre actuale 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) prin Europa în locul cifrelor romane (I, II, III, IV, V etc.). Asta ne-a salvat pe toți o mulțime de probleme! Mulțumesc, Leonardo.

Ziua Fibonacci
Ziua Fibonacci este 23 noiembrie, deoarece are cifrele „1, 1, 2, 3” care face parte din secvență. 23 noiembrie să știe toată lumea!


Leave a Reply