graficul unei inegalități liniare într-o variabilă este o linie numerică. Se utilizează un cerc deschis pentru< și> și un cerc închis pentru articolele de la numărul de telefon și de la numărul de telefon.

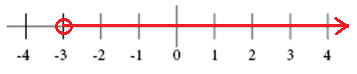
graful pentru X> -3

graful pentru x inkt 2

inegalități care au aceeași soluție se numesc echivalente. Există proprietăți ale inegalităților, precum și proprietăți ale egalității. Toate proprietățile de mai jos sunt, de asemenea, valabile pentru inegalitățile care implică articolele de la art.

proprietatea de adăugare a inegalității spune că adăugarea aceluiași număr la fiecare parte a inegalității produce o inegalitate echivalentă

$$If \: X>y,\: atunci\: x+Z>y+z$$

$$If\: X<Y,\: atunci\: x + z<y+z$$

proprietatea de scădere a inegalității ne spune că scăderea aceluiași număr din ambele părți ale unei inegalități dă o inegalitate echivalentă.

$$Dacă \: x>y,\: atunci\: x-z>y-z$$

$$Dacă\: x<y,\: atunci\: x-z<y-z$$

proprietatea de multiplicare a inegalității ne spune că înmulțirea pe ambele părți ale unei inegalități cu un număr pozitiv produce o inegalitate echivalentă.

$ $ Dacă\: x > y\: și\: z>0,\: atunci\: xz>yz$$

$$Dacă\: x<y\: și\: z>0,\: apoi\: XZ<YZ$$

înmulțirea în fiecare parte a unei inegalități cu un număr negativ pe de altă parte nu produce o inegalitate echivalentă decât dacă inversăm și direcția simbolului inegalității

$$dacă \: X>y \: și\: Z<0,\: atunci\: XZ<YZ$$

$$dacă\: x<Y\: și\: z <0,\: atunci\: xz> yz$$

același lucru este valabil și pentru proprietatea de divizare a inegalității.împărțirea ambelor părți ale unei inegalități cu un număr pozitiv produce o inegalitate echivalentă.

$$Dacă \: x>y \: și\: z>0,\: atunci\: \frac{x}{z}>\frac{y}{z}$$

$$Dacă\: x<Y\: și\: z>0,\: atunci\: \frac{x}{z} <\frac{y}{z}$$

și diviziunea pe ambele părți ale unei inegalități cu un număr negativ produce o inegalitate echivalentă dacă simbolul inegalității este inversat.

$$Dacă \: x>y \: și\: z<0,\: atunci\: \frac{x}{z}<\frac{y}{z}$$

$$Dacă\: x<Y\: și\: z<0,\: apoi\: \frac{x}{z}>\frac{y}{z}$$

pentru a rezolva o inegalitate în mai mulți pași, faceți așa cum ați făcut atunci când rezolvați ecuații în mai mulți pași. Luați un lucru la momentul de preferință începând prin izolarea variabilei de constante. Atunci când rezolvați inegalitățile în mai multe etape, este important să nu uitați să inversați semnul inegalității atunci când înmulțiți sau împărțiți cu numere negative.

exemplu

rezolva inegalitatea

$$-2 \ stânga (x + 3 \ dreapta) < 10$$