Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Introducere
rădăcinile pătrate sunt cel mai adesea scrise folosind un semn radical, ca acesta,![]() . Dar există un alt mod de a reprezenta luarea unei rădăcini. Puteți folosi exponenți raționali în locul unui radical. Un exponent rațional este un exponent care este o fracțiune. De exemplu,
. Dar există un alt mod de a reprezenta luarea unei rădăcini. Puteți folosi exponenți raționali în locul unui radical. Un exponent rațional este un exponent care este o fracțiune. De exemplu, ![]() poate fi scris ca
poate fi scris ca ![]() .
.
nu vă puteți imagina ridicând un număr la un exponent rațional? Poate fi greu să te obișnuiești, dar exponenții raționali pot ajuta de fapt la simplificarea unor probleme. Să explorăm relația dintre exponenții raționali (fracționari) și radicali.
rescrierea expresiilor radicale folosind exponenți raționali
radicalii și exponenții fracționari sunt modalități alternative de exprimare a aceluiași lucru. Ați văzut deja cum rădăcinile pătrate pot fi exprimate ca un exponent al puterii de o jumătate.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Amintiți-vă, cubarea unui număr îl ridică la puterea a trei. Observați că în aceste exemple, numitorul exponentului rațional este numărul 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and exponenți raționali: și anume, că a n-a rădăcină a unui număr poate fi scrisă fie ca ![]() sau
sau ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an expresie care conține un exponent rațional, îl puteți rescrie folosind un radical. În tabelul de mai sus, observați cum numitorul exponentului rațional determină indicele rădăcinii. Deci, un exponent al ![]() se traduce la rădăcina pătrată, un exponent al
se traduce la rădăcina pătrată, un exponent al ![]() se traduce la a cincea rădăcină sau
se traduce la a cincea rădăcină sau ![]() și
și ![]() se traduce la a opta rădăcină sau
se traduce la a opta rădăcină sau ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
rescrieți expresia cu exponentul fracțional ca radical. Numitorul fracției determină rădăcina, în acest caz rădăcina cubului. parantezele din |
|
|
răspuns |
|
|
amintiți-vă că exponenții se referă numai la cantitatea imediat la stânga lor, cu excepția cazului în care se utilizează un simbol de grupare. Exemplul de mai jos arată foarte asemănător cu exemplul anterior, cu o diferență importantă—nu există paranteze! Uite ce se întâmplă.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Numitorul fracției determină rădăcina, în acest caz rădăcina cubului. exponentul se referă numai la partea expresiei imediat la stânga exponentului, în acest caz x, dar nu 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. În acest caz, indicele radicalului este 3, deci exponentul rațional va fi deoarece 4 este în afara radicalului, nu este inclus în simbolul grupării și exponentul nu se referă la acesta. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
răspuns |
|
|
exponenți raționali cu numărători, alții decât unul
toți numeratorii pentru exponenții fracționari din exemplele de mai sus au fost 1. Puteți utiliza exponenți fracționari care au numărători, alții decât 1, pentru a exprima rădăcinile, așa cum se arată mai jos. Observați orice tipare în cadrul acestui tabel?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
pentru a rescrie un radical folosind un exponent fracționat, puterea la care radicandul este ridicat devine numărătorul și rădăcina devine numitorul.
scrierea exponenților fracționari
orice radical în forma![]() poate fi scris folosind un exponent fracțional în forma
poate fi scris folosind un exponent fracțional în forma![]() .
.
relația dintre![]() și
și![]() funcționează și pentru exponenții raționali care au un numărător de 1. De exemplu, radicalul
funcționează și pentru exponenții raționali care au un numărător de 1. De exemplu, radicalul ![]() poate fi scris și ca
poate fi scris și ca ![]() , deoarece orice număr rămâne aceeași valoare dacă este ridicat la prima putere. Acum Puteți vedea de unde vine numărătorul lui 1 în forma echivalentă a
, deoarece orice număr rămâne aceeași valoare dacă este ridicat la prima putere. Acum Puteți vedea de unde vine numărătorul lui 1 în forma echivalentă a ![]() .
.
simplificarea expresiilor radicale folosind exponenți raționali și legile exponenților
să explorăm câteva expresii radicale acum și să vedem cum să le simplificăm. Iată o expresie radicală care trebuie simplificată, ![]() .
.
o metodă de simplificare a acestei expresii este factorul și extragerea grupurilor de a3, așa cum se arată mai jos în acest exemplu.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
răspuns |
|
|
de asemenea, puteți simplifica această expresie gândindu-vă la radical ca o expresie cu un exponent rațional și folosind principiul că orice radical sub forma ![]() poate fi scris folosind un exponent fracțional în forma
poate fi scris folosind un exponent fracțional în forma ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
ambele metode de simplificare au dat același rezultat, a2. În funcție de contextul problemei, poate fi mai ușor să utilizați o metodă sau alta, dar deocamdată, veți observa că ați reușit să simplificați această expresie mai rapid folosind exponenți raționali decât atunci când utilizați metoda „extragere”.
să încercăm un alt exemplu.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the exponent rațional înapoi la forma radicală. |
|
|
răspuns |
|
|
din nou, metoda alternativă este de a lucra la simplificarea sub radical prin utilizarea factoring. Pentru exemplul pe care tocmai l-ați rezolvat, arată așa.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
să încercăm o expresie mai complicată, ![]() . Această expresie are două variabile, o fracțiune și un radical. Să o luăm pas cu pas și să vedem dacă utilizarea exponenților fracționari ne poate ajuta să o simplificăm.
. Această expresie are două variabile, o fracțiune și un radical. Să o luăm pas cu pas și să vedem dacă utilizarea exponenților fracționari ne poate ajuta să o simplificăm.
să începem prin simplificarea numitorului, deoarece aici se află semnul radical.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Prin convenție, o expresie nu este de obicei considerată simplificată dacă are un exponent fracțional sau un radical în numitor. |
||
|
răspuns |
|
||
ei bine, asta a durat ceva, dar ai făcut-o. Ați aplicat ceea ce știți despre exponenții fracționari, exponenții negativi și regulile exponenților pentru a simplifica expresia.
rezumat
un radical poate fi exprimat ca o expresie cu un exponent fracțional urmând Convenția![]() . Rescrierea radicalilor folosind exponenți fracționari poate fi utilă în simplificarea unor expresii radicale. Când lucrați cu exponenți fracționari, amintiți-vă că exponenții fracționari sunt supuși tuturor acelorași reguli ca și alți exponenți atunci când apar în expresii algebrice.
. Rescrierea radicalilor folosind exponenți fracționari poate fi utilă în simplificarea unor expresii radicale. Când lucrați cu exponenți fracționari, amintiți-vă că exponenții fracționari sunt supuși tuturor acelorași reguli ca și alți exponenți atunci când apar în expresii algebrice.
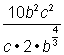
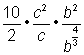
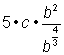
Leave a Reply