odată cu succesul la box-office al filmului „interstelar”, mulți oameni sunt încântați de perspectivele găurilor de vierme ca mijloc de transport interstelar. Deși în prezent nu există dovezi că astfel de obiecte exotice există în natură, este posibil ca acestea să poată fi create artificial, probabil din versiuni ale teoriei corzilor dimensionale superioare și ale ingineriei spumei fundamentale spațiu-timp. Cercetarea găurilor de vierme este astăzi un subiect interesant, cu zeci de lucrări publicate în reviste evaluate de colegi în fiecare an, dar merită amintit de originile sale-și începe dintr — un loc surprinzător.în 1915, Albert Einstein și-a publicat teoria generală a relativității, descrierea gravitației care definește perfect modul în care obiectele se vor atrage reciproc și vor afecta spațiul și timpul din jurul lor. Mulți ani mai târziu, fizicianul american John Wheeler a inventat expresia „spațiul spune materiei cum să se miște și materia spune spațiului cum să se curbeze”. Einstein a descris gravitația ca o manifestare a curburii spațiu-timp. Relativitatea generală este o teorie a câmpului continuu în contrast cu teoria particulelor materiei care a dus la mecanica cuantică.

Einstein a fost, de asemenea, implicat în dezvoltarea mecanicii cuantice, teoria care descrie particulele subatomice. Dar nu era pe deplin mulțumit de incertitudinile sale inerente și de caracterul probabilistic. Deci, în 1935, a lucrat cu Nathan Rosen pentru a produce o teorie a câmpului pentru electroni, folosind relativitatea generală. Lucrarea lor a fost intitulată”problema particulelor în teoria generală a relativității”. Einstein și Rosen investigau posibilitatea unei teorii atomiste a materiei și electricității care, excluzând discontinuitățile (singularitățile) din domeniu, nu a folosit alte variabile decât descrierea (metrica) relativității generale și teoria electromagnetică a lui Maxwell. Una dintre consecințe a fost că cea mai elementară particulă încărcată s-a dovedit a fi una de masă zero.

în cele din urmă, ceea ce au produs a fost ceva destul de original. Au început cu ecuațiile pentru o distribuție de masă sferică simetrică, deja utilizată pentru găurile negre și cunoscută sub numele de soluția Schwarzschild,

$$ds^2 = -\dfrac{1}{1-2m/r}dr^2 – R^2(d\theta^2+\sin^2\theta d\phi^2) + (1-2m/r)dt^2$$

unde \(ds^2\) este metrica și \(m=GM/C^2\) cu coordonate sferice \((r,\Theta,\Phi)\) și timp \(t\).

au efectuat o transformare de coordonate pentru a elimina regiunea care conține singularitatea curburii, o discontinuitate în curbura spațiului implicată de găurile negre și fenomene similare. Singularitatea la \(r=2M\) a fost eliminată prin transformarea coordonatelor \(u^2 = r – 2M\), rezultând o soluție finală,

$$DS^2 = -4(u^2 + 2M)du^2 – (u^2 + 2M)^2 D\Omega^2 + \dfrac{u^2}{u^2 + 2M} dt^2$$

unde \(D\Omega^2 = D\theta^2 + \Sin^2\theta d\PHI^2\).

această soluție a fost o reprezentare matematică a spațiului fizic printr-un spațiu de două foi asimptotic plate conectate printr-un pod sau o gaură de vierme Schwarzschild cu un ‘gât’. Aceasta conectează cele două foi și, prin analogie, două părți separate ale universului real, tridimensional. Figura 1 arată spațiul din jurul găurii de vierme, spațiul de deasupra și de dedesubt devenind plat la „margini” pe măsură ce măriți la infinit.

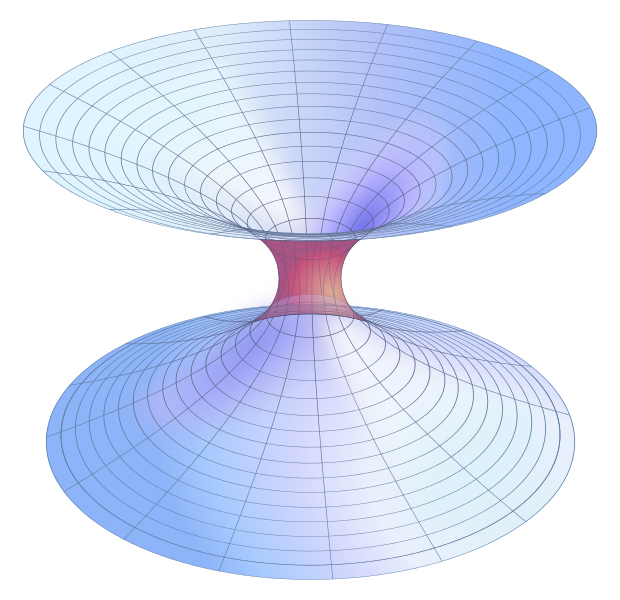
acum, aceasta nu a fost o gaură de vierme traversabilă, pentru că a trebuit să așteptăm sosirea Fizicienilor John Wheeler în anii 1950 și Kip Thorne în anii 1980. În 1987, cu încurajarea lui Carl Sagan pentru romanul său „Contact” (mai târziu un lungmetraj), Thorne și colegul său Michael Morris au reușit să construiască o descriere matematică, o metrică, pentru a descrie o gaură de vierme sferică simetrică și statică cu o circumferință reală, finită. Aceasta a avut o coordonată care a scăzut de la infinit negativ — în spațiu minim curbat-la o valoare minimă în care a fost localizat gâtul și apoi a crescut de la gât la infinit pozitiv — într — un spațiu diferit minim curbat. Această soluție are caracteristica distinctivă de a nu avea orizont de evenimente — spre deosebire de o gaură neagră. Lucrarea lui Thorne și Morris a fost intitulată”găurile de vierme în spațiu-timp și utilizarea lor pentru călătoriile interstelare: un instrument pentru predarea Relativității Generale”. Această lucrare a ajutat la stabilirea cercetării găurilor de vierme ca un nou domeniu de cercetare academică.

de atunci, au fost publicate multe lucrări și, într-adevăr, au fost efectuate sondaje astronomice, examinând cele mai îndepărtate stele și galaxii în căutarea găurilor de vierme naturale. Nici unul nu a fost identificat încă, dar amintiți — vă originea acestui domeniu de cercetare-Podul Einstein-Rosen nu a fost o gaură de vierme traversabilă și nu a fost intenția autorului de a produce una, totuși au produs prima descriere matematică a unei găuri de vierme. Ar trebui să fie amintiți pentru asta. Cercetarea științifică produce adesea ceva destul de neașteptat, cu implicații care depășesc cu mult intențiile inițiale ale cercetătorilor.

Kelvin F. De mult timp

de când a fost publicat acest articol, revista noastră, Principium, a publicat două numere (numerele 9& 10) în care discutăm mai detaliat găurile de vierme și Podul Einstein-Rosen. Aceste aspecte detaliază, de asemenea, Simpozionul de o zi pe tema „găurile de vierme interstelare: fizică și realizare practică” organizat de inițiativa pentru studii interstelare în colaborare cu societatea interplanetară Britanică.