Articles

permutări și combinații ușoare

by admin

întotdeauna am confundat „permutarea” și „combinația” — care dintre ele?

Iată o modalitate ușoară de a vă aminti: permutarea sună complicată, nu-i așa? Și este. Cu permutări, fiecare mic detaliu contează. Alice, Bob și Charlie este diferit de Charlie, Bob și Alice (introduceți numele prietenilor dvs. aici).

combinațiile, pe de altă parte, sunt destul de ușoare. Detaliile nu contează. Alice, Bob și Charlie este la fel ca Charlie, Bob și Alice.

permutările sunt pentru liste (ordinea contează) și combinațiile sunt pentru grupuri (ordinea nu contează).

știi, o „blocare combinație” ar trebui să fie într-adevăr numit un „blocare permutare”. Ordinea în care pui numerele contează.

permutări și combinații ușoare

o adevărată „blocare combinată” ar accepta atât 10-17-23, cât și 23-17-10 ca fiind corecte.

permutări: detaliile păroase

să începem cu permutări sau toate căile posibile de a face ceva. Folosim termenul „permutare”, așa că ne va păsa de fiecare detaliu, inclusiv ordinea fiecărui articol. Să presupunem că avem 8 persoane: 

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

În câte moduri putem acorda un premiu 1, 2 și 3 între opt concurenți? (Aur / Argint / Bronz)

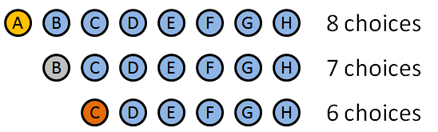
exemplu de permuare medalii

vom folosi permutări deoarece ordinea în care înmânăm aceste medalii contează. Iată cum se descompune:

  • medalie de aur: 8 alegeri: A B C D E F G H (inteligent cum am făcut numele se potrivesc cu litere, nu-i așa?). Să spunem că A câștigă aurul.
  • medalie de argint: 7 alegeri: B C D E F G H. să presupunem că B câștigă argintul.
  • medalie de bronz: 6 alegeri: C D E F G H. să spunem… c câștigă bronzul.

am ales anumite persoane pentru a câștiga, dar detaliile nu contează: am avut 8 opțiuni la început, apoi 7, apoi 6. Numărul total de opțiuni a fost $8 * 7 * 6 = 336$.

să ne uităm la detalii. A trebuit să comandăm 3 persoane din 8. Pentru a face acest lucru, am început cu toate opțiunile (8), apoi le-am luat pe rând (7, apoi 6) până când am rămas fără medalii.

știm că factorialul este:

\ displaystyle{ 8! = 8 \ cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 }

Din păcate, asta face prea mult! Vrem doar $8 * 7 * 6$. Cum putem „opri” factorialul la 5?

aici permutările se răcesc: observați cum vrem să scăpăm $5 * 4 * 3 * 2 * 1$. Care este un alt nume pentru asta? 5 factorial!

deci, dacă facem 8!/5! obținem:

\ displaystyle {\frac{8!}{5!} = \ frac{8 \cdot 7 \ cdot 6 \ cdot 5 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \ cdot 6}

și de ce am folosit numărul 5? Pentru că a rămas după ce am ales 3 medalii din 8. Deci, o modalitate mai bună de a scrie acest lucru ar fi:

\displaystyle{\frac{8!}{(8-3)!}}

unde 8!/(8-3)! este doar un mod fantezist de a spune „utilizați primele 3 numere de 8!”. Dacă avem n total articole și dorim să alegem k într-o anumită ordine, obținem:

\displaystyle{\frac{n!} {(n-k)!}}

și aceasta este formula de permutare fantezistă: aveți n articole și doriți să găsiți numărul de moduri în care pot fi comandate k articole:

\displaystyle{p(n,k) = \frac{n!} {(n-k)!}}

combinații, Ho!

combinațiile sunt ușor merge. Ordinea nu contează. Puteți să-l amestecați și arată la fel. Să spunem că sunt un zgârcit și nu-mi pot permite medalii separate de aur, argint și bronz. De fapt, îmi permit doar cutii goale de tablă.

în câte moduri pot da 3 cutii de conserve la 8 persoane?Ei bine ,în acest caz, ordinea în care alegem oamenii nu contează. Dacă îi dau o cutie lui Alice, Bob și apoi lui Charlie, este la fel ca să-i dau lui Charlie, Alice și apoi lui Bob. Oricum ar fi, sunt la fel de dezamăgiți.

Acest lucru ridică un punct interesant — avem câteva concedieri aici. Alice Bob Charlie = Charlie Bob Alice. Pentru o clipă, să ne dăm seama în câte moduri putem rearanja 3 persoane.Ei bine, avem 3 opțiuni pentru prima persoană, 2 pentru a doua și doar 1 pentru ultima. Deci avem $3 * 2 * 1 $ moduri de a re-aranja 3 persoane.

stai puțin… asta seamănă puțin cu o permutare! M-ai păcălit!

într-adevăr am făcut-o. Dacă aveți n oameni și doriți să știți câte aranjamente există pentru toți, este doar n factorial sau n!

deci, dacă avem 3 cutii de conserve pentru a da, există 3! sau 6 variante pentru fiecare alegere pe care o alegem. Dacă vrem să ne dăm seama câte combinații avem, creăm doar toate permutările și împărțim la toate redundanțele. În cazul nostru, obținem 336 permutări (de sus) și împărțim la cele 6 redundanțe pentru fiecare permutare și obținem 336/6 = 56.

formula generală este

\displaystyle{C(n,k) = \frac{P(N,k)}{k!}}

ceea ce înseamnă „găsiți toate căile de a alege k oameni din n, și împărțiți cu k! variante”. Scriind acest lucru, obținem formula noastră de combinație sau numărul de moduri de a combina elementele k dintr-un set de n:

\displaystyle{c(n,k) = \frac{n!} {(n-k)!k!}}

uneori C(n,k) este scris ca:

\displaystyle{\binom {n}{k}}

care este coeficientul binomial.

câteva exemple

iată câteva exemple de combinații (ordinea nu contează) din permutări (ordinea contează).

  • combinație: alegerea unei echipe de 3 persoane dintr-un grup de 10. $C ( 10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

    permutare: alegerea unui președinte, VP și Waterboy dintr-un grup de 10. $P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.

  • combinație: alegerea a 3 deserturi dintr-un meniu de 10. C ( 10,3) = 120.

    permutare: listarea dvs. 3 deserturi preferate, în ordine, dintr-un meniu de 10. P ( 10,3) = 720.

nu memorați formulele, înțelegeți de ce funcționează. Combinațiile sună mai simplu decât permutările și sunt. Aveți mai puține combinații decât permutări.

alte postări din această serie

  1. permutări și combinații ușoare
  2. navigați într-o grilă folosind combinații și permutări
  3. cum să înțelegeți combinațiile folosind multiplicarea
  4. De ce multiplicăm combinațiile?