o problemă veche va da o nouă perspectivă? Poate o dovadă elegantă a teoremei 4 culori?
problema cu 4 culori este una dintre cele mai cunoscute probleme matematice. A rezistat dovezilor mai mult de o sută de ani înainte de a ceda în cele din urmă; în cele din urmă, a existat o dovadă validă, dar una care s-a bazat pe mai mult de o mie de ore de timp pe computer. Cercetările lui Jim Tilley sugerează că o simplificare dramatică ar putea fi posibilă în cele din urmă. El a descoperit o proprietate, Kempe-locking, pe care trebuie să o prezinte un contraexemplu minim la teorema cu 4 culori și a formulat o presupunere, bazată pe investigații ample, că diamantul Birkhoff este singura configurație fundamentală de blocare Kempe.
colorarea grafurilor implică atribuirea de etichete sau culori vârfurilor unui obiect matematic cunoscut sub numele de grafic. Problema cu 4 culori a oferit una dintre motivațiile originale pentru dezvoltarea teoriei grafurilor algebrice. Colorarea graficelor este utilizată în multe probleme din lumea reală, cum ar fi minimizarea conflictelor la programarea evenimentelor sportive, planificarea orarelor de examinare și organizarea planurilor de ședere, chiar și pentru plasarea camerei CCTV într-o clădire cu multe colțuri, pentru a Minimiza suprapunerea camerei. Acesta oferă, de asemenea, fundamentul pentru puzzle-uri Sudoku.
problema cu 4 culori
Francis Guthrie, student al celebrului matematician și logician Britanic Augustus De Morgan, a pus problema cu 4 culori în 1852. El a formulat problema cu privire la hărțile care îndeplinesc anumite condiții, cum ar fi să nu conțină găuri și să aibă fiecare regiune (de exemplu, țară sau stat) conectată astfel încât să nu existe nicio regiune în două sau mai multe părți necontigue. Guthrie a susținut că pentru astfel de hărți nu ar fi nevoie niciodată de mai mult de patru culori pentru a colora harta astfel încât două regiuni învecinate să nu aibă aceeași culoare.
în zilele noastre, problema cu 4 culori este exprimată în termeni de grafice și, în loc să coloreze regiuni în Hărți, o culoare se transformă în vârfuri în grafice. Toate dovezile existente ale teoremei cu 4 culori demonstrează că nu poate exista un contraexemplu minim. (Un contraexemplu minim este cel mai mic grafic plan care necesită mai mult de patru culori pentru o colorare adecvată a vârfurilor sale.) Numai graficele plane care sunt triangulații trebuie luate în considerare, deoarece orice grafic care nu este o triangulare poate fi transformat într-unul prin inserarea marginilor. Dacă triangulația rezultată este 4-colorable, atunci graficul original este, de asemenea, 4-colorable. Este foarte util să poți restricționa examinarea cuiva la triangulații.

o încercare timpurie de a dovedi
a celor care au oferit o dovadă, Alfred Bray Kempe, un avocat englez și matematician Amator, a fost persoana a cărei reputație a fost cea mai afectată de efortul său eșuat. El și-a anunțat succesul în 1879, iar dovada sa a fost publicată în American Journal of Mathematics. Unsprezece ani mai târziu, însă, un alt matematician englez, Percy Heawood, a creat o hartă pe care a colorat-o în 4 până la regiunea finală, astfel încât metoda lui Kempe a eșuat pentru acea regiune finală. În ciuda eșecului său, Kempe a lăsat un instrument util-un lanț Kempe. Este un maxim, conectat (fiecare vârf accesibil de la oricare altul printr-o cale de-a lungul marginilor) subgraf în care toate vârfurile folosesc exact două culori. Lanțurile Kempe s-au dovedit a fi esențiale în colorarea și re-colorarea graficelor. A Se Vedea Figura 1.
ar fi o simplificare uluitoare
dacă diamantul Birkhoff singur este cheia pentru 4-colorabilitate. prima dovadă validă a fost anunțată în 1976 de Kenneth Appel și Wolfgang Haken. A fost nevoie de peste o mie de ore de timp de calculator pentru a verifica anumite aspecte ale argumentului lor. Această noțiune de a se baza pe codul computerului, care conține potențial erori induse de om (și Codul lor a făcut-o!), mai degrabă decât o dovadă ‘umană’, nu a satisfăcut o mare parte a comunității matematice. Dovada lui Appel și Haken a fost elegantă în structura sa generală, dar detaliile au fost urâte. dovada a fost rafinată în 1996 de o echipă de patru matematicieni: Robertson, Sanders, Seymour și Thomas, dar ei s-au bazat încă pe codul computerului pentru a-și completa dovada. În 2010, Steinberger a oferit o altă variantă. Cu toate acestea, nu există încă un răspuns complet satisfăcător cu privire la motivul pentru care teorema 4 culori este adevărată. (Odată ce conjectura a fost dovedită, a câștigat statutul de teoremă.’)

căutarea unei dovezi alternative
problema cu 4 culori este atât de ușor de articulat și de înțeles încât a atras interesul multor mii de matematicieni amatori, toți crezând că pot găsi o dovadă clasică simplă și astfel pot deveni celebri. Tatăl lui Jim Tilley, fizician și director al Colegiului Militar Regal din Canada din 1978-1984, a fost un astfel de visător. Ori de câte ori simțea că a făcut o descoperire, îl ruga pe fiul său, Jim, să-i verifice munca. Jim a găsit întotdeauna un defect. Cu toate acestea, în ciuda scepticismului său inițial că eforturile tatălui său vor da vreodată roade, el s-a infectat cu un entuziasm pentru problema celor 4 culori și a început să o studieze intens.cercetările lui Jim Tilley au condus la descoperirea unei noi proprietăți pe care trebuie să o prezinte un contraexemplu minim la teorema 4 culori. L-a numit Kempe-locking. El și – a dat seama că este probabil să fie incompatibil cu o altă proprietate pe care trebuie să o prezinte un contraexemplu minim-și anume., cât de conectat este un grafic (câte vârfuri trebuie eliminate dintr-un grafic înainte de a se destrăma).
blocarea Kempe a lui Tilley este o proprietate asociată cu o margine într-o triangulare. Noțiunea începe cu ștergerea unei muchii xy între vârfurile adiacente x și y. Dacă pentru fiecare 4 culori a graficului rezultat în care culorile lui x și y sunt aceleași, nu există o secvență de schimburi de culori pe lanțurile Kempe care determină culoarea lui x să difere de culoarea lui y, atunci se spune că triangulația originală este blocată Kempe în raport cu marginea xy. Tilley a demonstrat că un contraexemplu minim la teorema 4 culori trebuie să fie blocat Kempe în raport cu fiecare dintre marginile sale; fiecare margine dintr-un contraexemplu minim trebuie să aibă această proprietate de colorare.Kempe-blocare este o condiție deosebit de restrictivă, care devine mai dificil de a satisface ca o triangulație devine mai mare. Tilley și-a propus să descopere dacă există ceva comun triangulațiilor care au margini blocate de Kempe. Cea mai timpurie căutare a lui Kempe-locking l-a dus la diamantul Birkhoff.

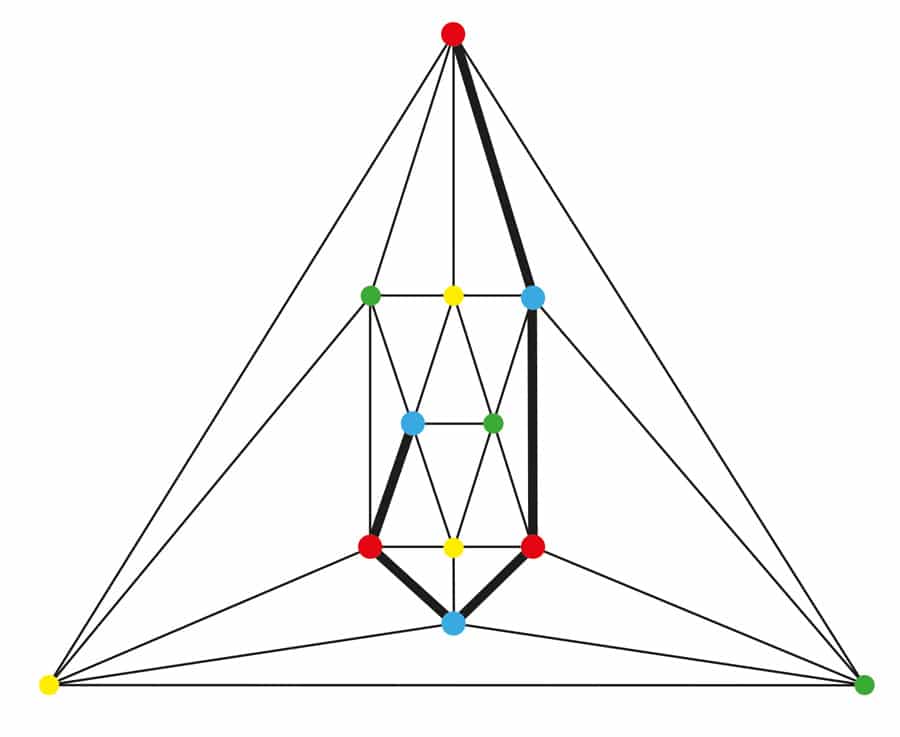
Figura 3. Două grafice plane, unul o triangulație cu 4 conexiuni pe 6 vârfuri și unul o triangulație cu 5 conexiuni pe 17 vârfuri.
diamantul Birkhoff
În 1913, G. D. Birkhoff a descoperit că o anumită configurație a zece țări într-o hartă (un inel de graniță din șase țări care cuprinde un set de patru țări) are o proprietate importantă. Dacă această configurație este prezentă într-o hartă și dacă submap-ul cu acea configurație eliminată este 4-colorable, atunci întreaga hartă va fi 4-colorable. Astfel, un contraexemplu minim nu poate conține acea configurație particulară. A ajuns să fie cunoscut sub numele de diamantul Birkhoff. Tilley a descoperit că o margine XY blocată de Kempe pare să apară numai atunci când x și y sunt, de asemenea, punctele finale ale versiunii grafice a unui diamant Birkhoff. A Se Vedea Figura 2.
conjectura este ușor de declarat, ușor de înțeles, și intrigant, și oferă o explicație convingătoare pentru ce toate graficele plane sunt 4-colorable.
neavând nicio configurație de blocare Kempe fără un diamant Birkhoff, el a presupus că diamantul Birkhoff este singura configurație fundamentală de blocare Kempe, una care nu conține o configurație mai mică de blocare Kempe ca subgraf. Cu toate acestea, Tilley a constatat că nu și-a putut dovedi conjectura critică. A fost frustrant pentru că, dacă este adevărat, conjectura ar dovedi direct Teorema celor 4 culori. (Pentru a fi un contraexemplu minim, o triangulare ar trebui să conțină un subgraf de diamant Birkhoff, dar dacă a făcut-o, nu ar putea fi un contraexemplu minim.)
un caz de sprijin copleșitor
în loc să-și dovedească presupunerea, Tilley a făcut următorul lucru cel mai bun. El a decis să joace rolul unui experimentalist și să construiască un caz copleșitor pentru a-și susține conjectura. El a împărțit toate triangulațiile plane relevante în două clase: Cele în care cel puțin patru vârfuri trebuie îndepărtate înainte ca graficele să se destrame (4-conectate) și cele în care cel puțin cinci vârfuri trebuie îndepărtate înainte ca grafurile să se destrame (5-conectate). A Se Vedea Figura 3. Util în căutarea extinsă a lui Tilley a fost că a trebuit să examineze doar un membru al fiecărei clase de izomorfism (grafice care sunt identice din punct de vedere structural). Tilley a examinat toate cele 8.044 de clase de izomorfism cu 4 triangulații plane conectate pe până la 15 vârfuri și toate cele 9.733 de clase de izomorfism cu 5 triangulații plane conectate pe până la 24 de vârfuri. A găsit doar trei triangulații blocate de Kempe. Fiecare margine descoperită blocată de Kempe avea un diamant Birkhoff și fiecare a avut loc într-o triangulare cu 4 conexiuni. Nu au existat deloc între triangulațiile conectate la 5.

Tilley și-a extins căutarea printre triangulațiile 4 conectate examinând toate cele 30.926 de clase de izomorfism pe 16 vârfuri și toate cele 158.428 de clase de izomorfism pe 17 vârfuri. Limitările de timp de calcul au însemnat restricționarea căutării sale la eșantioane de 100.000 de triangulații non-izomorfe generate aleatoriu fiecare pentru clase pe 18,19 și 20 de vârfuri. Căutarea extinsă a generat 45 de triangulații suplimentare blocate de Kempe, dar exact aceleași rezultate ca și căutarea inițială: fiecare margine blocată de Kempe dintr-o triangulare a prezentat un diamant Birkhoff asociat.
De unde de aici? căutările extinse ale lui Tilley au confirmat cu ușurință că diamantul Birkhoff este o configurație fundamentală de blocare Kempe. El și-a testat temeinic conjectura, dar rămâne nedovedită. Dacă (sau când) conjectura lui Tilley se dovedește adevărată, adică că diamantul Birkhoff singur este cheia 4-colorabilitate, ar fi o simplificare uluitoare a problemei: o singură configurație care explică totul – eleganță matematică.

dovedirea conjecturii în 4 culori a necesitat eforturile multor matematicieni proeminenți. Presupunerea lui Tilley că diamantul Birkhoff este singura configurație fundamentală de blocare Kempe poate fi și mai dificil de dovedit. Cu toate acestea, dovezile experimentale sunt puternice. Teoreticienii ar putea spune ‘de ce deranjez?”Răspunsul lui Tilley este că curiozitatea insațiabilă va câștiga:” la urma urmei, conjectura este ușor de declarat, de înțeles și intrigantă și oferă o explicație convingătoare pentru motivul pentru care toate graficele plane sunt 4-colorable.”
răspuns Personal
ce v-a determinat inițial entuziasmul pentru problema celor 4 culori și v-a determinat să o studiați atât de intens?
a fost obsesia tatălui meu cu problema pensionării sale și dorința lui de a mă folosi ca placa de sondare pentru ideile sale.
care sunt planurile dvs. de cercetare viitoare în acest domeniu?
am revizuit recent o lucrare complicată care implică o abordare complet diferită a problemei 4-Color. După cum stă hârtia, cred că are defecte. Cu toate acestea, are promisiune. Aș putea fi tentat să explorez o colaborare.
Leave a Reply