numere complexe: introducere (pagina 1 din 3)

secțiuni: Introducere, operații cu complexe, formula pătratică

până acum, ți s-a spus că nu poți lua rădăcina pătrată a unui număr negativ. Asta pentru că nu aveai numere negative după ce le-ai pătrat (deci nu puteai „merge înapoi” luând rădăcina pătrată). Fiecare număr a fost pozitiv după ce l-ai pătrat. Deci, nu ai putea foarte bine pătrat-rădăcină un negativ și se așteaptă să vină cu ceva sensibil.acum, cu toate acestea, puteți lua rădăcina pătrată a unui număr negativ, dar implică utilizarea unui număr nou pentru a face acest lucru. Acest nou număr a fost inventat(descoperit ?) în perioada Reformei. La acea vreme, nimeni nu credea că se va găsi vreo utilizare „din lumea reală” pentru acest nou număr, în afară de facilitarea calculelor implicate în rezolvarea anumitor ecuații, astfel încât noul număr a fost privit ca fiind un număr prefăcut inventat de dragul comodității.

(dar atunci, când te gândești la asta, nu sunt toate numerele invenții? Nu e ca și cum numerele cresc în copaci! Ei trăiesc în capul nostru. Le-am inventat pe toate! De ce să nu inventăm unul nou, atâta timp cât funcționează bine cu ceea ce avem deja?)

apoi:

acum, ați putea crede că puteți face acest lucru:

dar acest lucru nu are nici un sens! Aveți deja două numere care pătrat la 1; și anume -1 și +1. Și am deja pătrate la -1. Deci, nu este rezonabil ca mi-ar, De asemenea, pătrat la 1. Acest lucru subliniază un detaliu important: Când ai de-a face cu imaginarii, câștigi ceva (capacitatea de a face față negativelor din interiorul rădăcinilor pătrate), dar pierzi și ceva (o parte din flexibilitatea și regulile convenabile pe care le aveai atunci când aveai de-a face cu rădăcinile pătrate). În special, trebuie să faceți întotdeauna partea i mai întâi!

• simplifica sqrt(-9). Drepturi de autor: Elizabeth Stapel 2000-2011 Toate drepturile rezervate

(avertisment: pasul care trece prin al treilea semn „egal” este ” „, nu „„. Eu este în afara radicalului.)

• Simplificați sqrt(-25).

• Simplificați sqrt(-18).

• Simplificați –sqrt(-6).

în calculele dvs., vă veți ocupa de i la fel cum ați face cu x, cu excepția faptului că x2 este doar x2, dar i2 este -1:

• Simplificați 2i + 3i.

2i + 3i = (2 + 3)I = 5I

• simplificați 16I – 5I.

16i – 5i = (16 – 5)i = 11i

• înmulțiți și simplificați (3i)(4i).

(3i) (4i) = (3·4) (i·i) = (12) (i2) = (12)(-1) = -12

• înmulțiți și simplificați (i) (2i) (–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

rețineți această ultimă problemă. În cadrul acestuia, puteți vedea că , deoarece i2 = -1. Continuând, obținem:

acest model de puteri, semne, 1, și i este un ciclu:

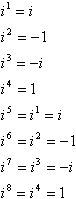
cu alte cuvinte, pentru a calcula orice putere mare de i, puteți converti la o putere mai mică de luând cel mai apropiat multiplu de 4 care nu este mai mare decât exponentul și scăzând acest multiplu din exponent. De exemplu, o întrebare truc obișnuită la teste este ceva de genul „Simplificați i99”, ideea fiind că veți încerca să multiplicați i nouăzeci și nouă de ori și veți rămâne fără timp, iar profesorii vor primi un chicotit bun pe cheltuiala dvs. în salonul Facultății. Iată cum funcționează comanda rapidă:

i99 = I96+3 = i(4 24)+3 = i3 = –i

adică i99 = i3, pentru că poți doar să tai i96. (Nouăzeci și șase este un multiplu de patru, deci i96 este doar 1, pe care îl puteți ignora.) Cu alte cuvinte, puteți împărți exponentul la 4 (folosind diviziunea lungă), aruncați răspunsul și utilizați doar restul. Acest lucru vă va oferi partea exponentului de care vă pasă. Iată câteva exemple:

• Simplificați i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = I

• Simplificați I120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• Simplificați I64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>