evaluarea Kappa lui Cohen

valoarea pentru kappa poate fi mai mică de 0 (negativ). Un scor de 0 înseamnă că există un acord aleatoriu între evaluatori, în timp ce un scor de 1 înseamnă că există un acord complet între evaluatori. Prin urmare, un scor mai mic de 0 înseamnă că există mai puțin acord decât șansa aleatorie. Mai jos, vă voi arăta formula pentru a rezolva acest lucru, dar este important să vă familiarizați cu figura 4 pentru a avea o înțelegere puternică.

Figura 4: N x n grid folosit pentru a interpreta rezultatele evaluatorilor

motivul pentru care am evidențiat două grile va deveni clar într-o clipă, dar deocamdată, permiteți-mi să descompun fiecare grilă.

A => numărul total de instanțe despre care ambii evaluatori au spus că sunt corecte. Evaluatorii sunt de acord.

B=> numărul total de cazuri pe care Rater 2 le-a spus a fost incorect, dar Rater 1 a spus că sunt corecte. Acesta este un dezacord.

C=> numărul total de cazuri pe care evaluatorul 1 le-a spus a fost incorect, dar Evaluatorul 2 a spus că sunt corecte. Acesta este, de asemenea, un dezacord.

D => numărul total de instanțe despre care ambii evaluatori au spus că sunt incorecte. Evaluatorii sunt de acord.

pentru a elabora valoarea kappa, trebuie mai întâi să cunoaștem probabilitatea unui acord (acest lucru explică de ce am evidențiat diagonala acordului). Această formulă este derivată prin adăugarea numărului de teste în care evaluatorii sunt de acord, apoi împărțind-o la numărul total de teste. Folosind exemplul din Figura 4, aceasta ar însemna(A + D)/(A + B+ C+ D).

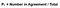
Figura 5: probabilitatea unui acord

perfect! Următorul pas este de a elabora probabilitatea unui acord aleatoriu. Folosind figura 4 ca un ghid, valoarea așteptată este numărul total de ori pe care Evaluator 1 a spus corect împărțit la numărul total de cazuri, înmulțit cu numărul total de ori pe care Evaluator 2 a spus corect împărțit la numărul total de cazuri, adăugat la numărul total de ori pe care Evaluator 1 a spus incorect înmulțit cu numărul total de ori pe care Evaluator 2 a spus incorect. Aceasta este o mulțime de informații pentru a lua acolo, astfel încât în Figura 6 am formulat această ecuație folosind grila de mai sus.

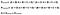
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

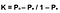
grozav! Acum puteți distinge între fiabilitate și validitate, explicați kappa lui Cohen și evaluați-o. Această statistică este foarte utilă, deși de când am înțeles cum funcționează, acum cred că poate fi subutilizată atunci când optimizăm algoritmi la o anumită metrică. În plus, kappa lui Cohen face, de asemenea, o treabă bună de măsurare atât a problemelor de clasă multi-clasă, cât și a celor dezechilibrate.

P. S. Dacă există ceva pe care doriți să acopere de a face cu știința datelor, puteți trimite-mi un mesaj pe Twitter @KurtisPykes sau lăsați un răspuns la acest post.