Integrale Definite
s-ar putea dori să citească Introducere în integrare în primul rând!
integrare
|
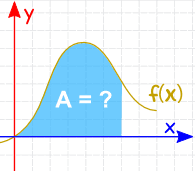
integrarea poate fi utilizată pentru a găsi zone, volume, puncte centrale și multe lucruri utile. Dar este adesea folosit pentru a găsi zona de sub graficul unei funcții ca aceasta: |
 |
|
|
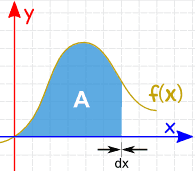
zona poate fi găsită adăugând felii care se apropie de zero în lățime: și există reguli de integrare care ne ajută să obținem răspunsul. |
 |
notație
Simbolul pentru „integral” este un „s” elegant (pentru „sumă”, ideea de a însuma felii):
după simbolul integral punem funcția pe care dorim să o găsim integrandul (numit integrand).
și apoi terminați cu dx pentru a însemna că feliile merg în direcția x (și se apropie de zero în lățime).
integrala definită
o integrală definită are valori de început și sfârșit: cu alte cuvinte, există un interval .
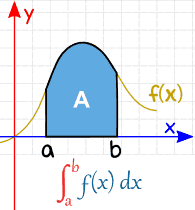
a și b (numite Limite, Limite sau limite) sunt puse în partea de jos și de sus a „S”, astfel:
 |
 |
|
| Definite Integral (from a to b) |
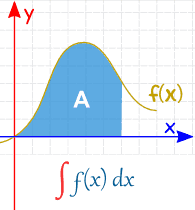
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
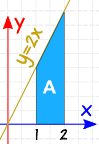
exemplu: ce este 2 x 1 2x DX
ni se cere integrala definita, de la 1 la 2, de 2x dx
Mai intai trebuie sa gasim integrala nedefinita integral.
folosind regulile de integrare constatăm că la X = X2 + c
se calculează acum că la 1, și 2:
- la x=1: 2x DX = 12 + C
- la x=2: 2x DX = 22 + C
scade:
și „C” este anulat … deci, cu integralele Definite putem ignora C.
rezultat:

verificați: cu o formă atât de simplă, să încercăm și să calculăm aria după geometrie:
a = 2+42 × 1 = 3
Da, are o suprafață de 3.
(ura!)
notație: Putem arăta integrala nedefinită (fără +C) în interiorul parantezelor pătrate, cu limitele a și b după, astfel:
exemplu (continuare)
o modalitate bună de a vă arăta răspunsul:
=
= 22 − 12
să încercăm un alt exemplu:
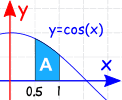
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
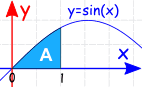
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
integrala nedefinită este: sin(x) + c
Din moment ce mergem de la 0, putem calcula integrala la x = 1?
−cos(1) = -0.540…
ce? Este negativ? Dar arată pozitiv în grafic.
Ei bine … am făcut o greșeală!
pentru că trebuie să scădem integrala la x=0. Nu ar trebui să presupunem că este zero.
deci, să o facem în mod corespunzător, scăzând unul din celălalt:
=
asta e mai bine!
dar putem avea regiuni negative, atunci când curba este sub axa:

exemplu:
integrala definita, de la 1 la 3, a cos(x) dx:
1
observați că unele dintre ele sunt pozitive, iar altele negative.
integrala definită va determina valoarea netă.
să facem calculele:
=
sin(3) − sin(1)
Salt este mai negativ decât pozitiv cu rezultatul net de -0.700….
deci avem acest lucru important de reținut:
încercați să integrați cos(x) cu valori diferite de început și Sfârșit pentru a vedea singuri cum funcționează pozitivele și negativele.
zona pozitivă
dar uneori dorim ca toată zona să fie tratată ca pozitivă (fără ca partea de sub axă să fie scăzută).
în acest caz trebuie să calculăm zonele separat, ca în acest exemplu:

exemplu: Care este suprafața totală dintre y = cos(x) și axa x, de la x = 1 la x = 3?
acesta este exemplul pe care tocmai l-am făcut, dar acum ne așteptăm ca toată zona să fie pozitivă (imaginați-vă că a trebuit să o pictăm).
deci, acum trebuie să facem părțile separat:
- una pentru zona de deasupra axei x
- una pentru zona de sub axa x
curba traversează axa x la X = hectolitru/2 deci avem:
de la 1 la hectolitru/2:
= Sin (2)-Sin (1)
de la 2 la 3:
= sin(3) − sin(Irak/2)
că ultima iese negativ, dar vrem să fie pozitiv, astfel:
suprafața totală = 0,159… + 0.859… = 1.018…
Acest lucru este foarte diferit de răspunsul din exemplul anterior.
continuu
o, da, funcția pe care o integrăm trebuie să fie continuă între a și b: fără găuri, salturi sau asimptote verticale (unde funcția se îndreaptă în sus / în jos spre infinit).
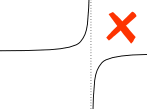
exemplu:
o asimptotă verticală între a și b afectează integrala definită.
proprietăți
zona de mai sus − zona de mai jos
integrala adaugă zona de deasupra axei, dar scade zona de mai jos, pentru o „valoare netă”:
funcții de adăugare
integrala lui f + g este egală cu integrala lui f plus integrala lui G:
a
inversarea intervalului
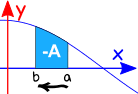
inversarea direcției intervalului dă negativul Direcției inițiale.
![]()

Leave a Reply