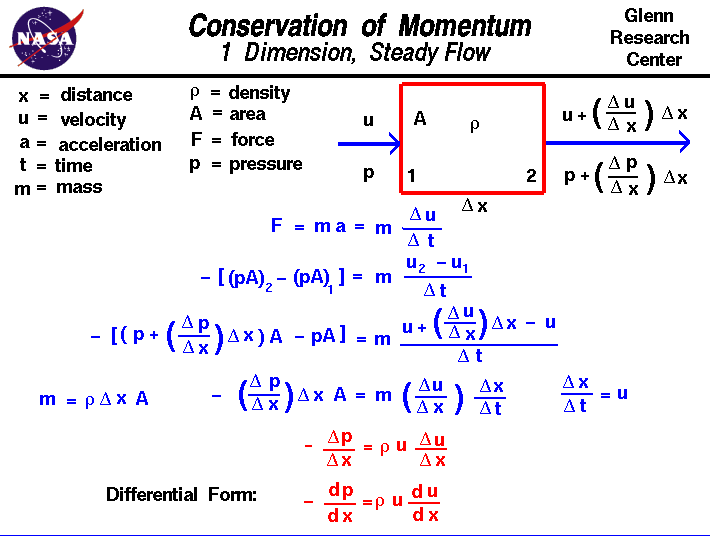
conservarea impulsului este un concept fundamental al fizicii, împreună cu conservarea energiei și conservarea masei.Impulsul este definit ca fiind masa unui obiect înmulțit cu vitezaa obiectului.Conservarea impulsului afirmă că, în cadrul unui domeniu problematic, cantitatea de impuls rămâne constantă;impulsul nu este nici creat, nici distrus, ci doar schimbat prin acțiunea forțelor așa cum este descris de legile mișcării lui Newton.A face față impulsului este mai dificil decât a face față masei și energiei, deoarecemomentul este cantitate avectorăavând atât o magnitudine, cât și o direcție. Impulsul este conservat în toate cele treidirecțiile fizice în același timp. Este și mai dificil atunci când avem de-a face cu agadeoarece forțele într-o direcție pot afecta impulsul într-o altă direcțiedin cauza coliziunilor multor molecule.Pe acest diapozitiv, vom prezenta o problemă de flux foarte, foarte simplificatăunde proprietățile se schimbă doar într-o singură direcție.Problema este simplificată și mai mult prin luarea în considerare a unui flux constant care nu se schimbă în timp și prin limitarea forțelor doar la cele asociate cu thepressure.Be conștient de faptul că problemele reale de flux sunt mult mai complexe decât acest exemplu simplu.să luăm în considerare fluxul unui gaz printr-un domeniu în care proprietățile de curgereschimbați doar într-o direcție, pe care o vom numi „x”. Gazul intră în stația domainat 1 cu o anumită viteză u și o anumită presiune pand iese la stația 2 cu o valoare diferită a vitezei și presiunii. Pentru simplitate, vom presupune astadensitatea r rămâne constantă în domeniuși că zona a prin care curge gazul rămâne, de asemenea, constantă. Locația stațiilor 1 și 2 sunt separatede la o distanță numită del x. (Delta este micul triunghi de pe glisantși este litera greacă „d”. Matematicienii folosesc adesea acest simbol pentru a denotao schimbare sau variație a unei cantități. Fontul web print nu acceptăliterele grecești, așa că o vom numi doar „del”.) O schimbare cu distanța este denumită a gradientpentru a evita confuzia cu o schimbare cu timpul care se numește rată.Gradientul de viteză este indicat de del u / del x; schimbarea vitezei perchange în distanță. Deci, la stația 2, viteza este dată de vitezăla 1 plus gradientul de ori distanța.

o expresie similară dă presiuneala ieșire:

a doua lege a mișcării lui Newton afirmă că forța F este egală cu schimbarea impulsului cu respectarea timpului. Pentru un obiect cu masă constantăm aceasta reduce la masa ori accelerația a.An accelerația este o schimbare a vitezei cu o schimbare a timpului(del u / del t). Apoi:

forța din această problemăvine din gradientul de presiune. Deoarece presiunea este o forță pe unitate de suprafață, forța netă pe domeniul nostru fluid este presiunea ori zona de la ieșire minus presiunea ori zona de la intrare.

semnul minus la începutul acestei expresii este folosit deoarece gazele se deplasează dintr-o regiune de presiune înaltă într-o regiune de presiune scăzută; dacă presiunea crește CUX, viteza va scădea. Înlocuind expresiile noastre pentru viteză și presiune:

Simplificați:

notând că (del x / del t) este vitalitatea și că masa este densitatea r ori volumul (aria ori del x):

simplificați:

del p / del X și Del u / del x reprezintă gradienții de presiune și viteză.Dacă ne micșorăm domeniul până la dimensiuni diferențiale, acești gradienți devin diferențiali:

aceasta este o formă unidimensională, constantă a Equation.It este interesant de remarcat faptul că căderea de presiunedin fluid (termenul din stânga) este proporțional atât cu valoarea velocității, cât și cu gradientul vitezei.O soluție a acestei ecuații de impuls ne oferă formapresiune dinamicăcare apare în ecuația lui Bernoulli.

activități:
tururi ghidate

• ecuații de dinamică a fluidelor de bază:

navigare ..

pagina principală a Ghidului începătorului