Introducere

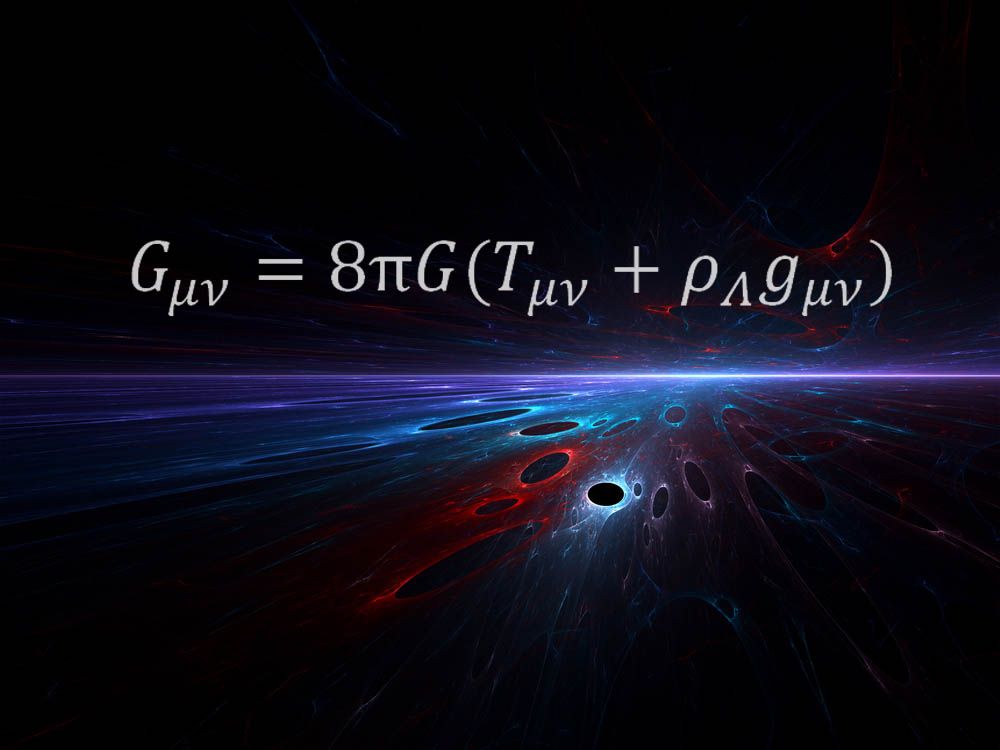
ecuațiile matematice nu sunt doar utile — multe sunt destul de frumoase. Și mulți oameni de știință recunosc că sunt adesea pasionați de anumite formule nu doar pentru funcția lor, ci pentru forma lor și adevărurile simple, poetice pe care le conțin.în timp ce anumite ecuații celebre, cum ar fi Albert Einstein E = mc^2, porc cea mai mare parte gloria publică, multe formule mai puțin familiare au campioni lor printre oamenii de știință. LiveScience a cerut Fizicienilor, astronomilor și matematicienilor ecuațiile lor preferate; iată ce am găsit:

relativitatea generală

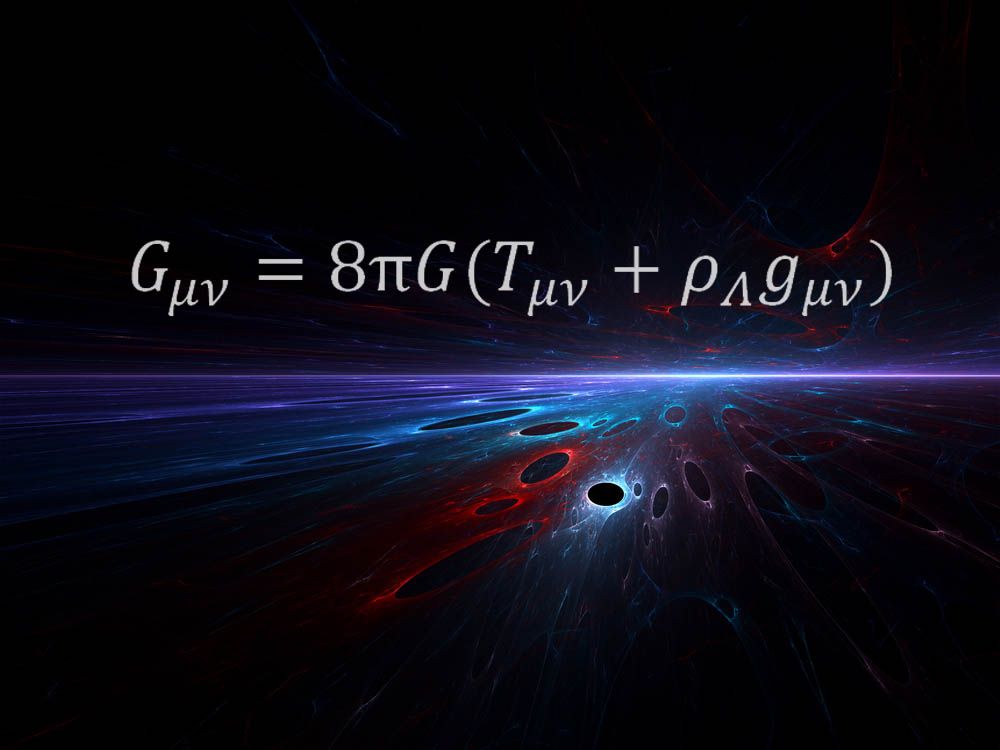
ecuația de mai sus a fost formulată de Einstein ca parte a teoriei generale a relativității în 1915. Teoria a revoluționat modul în care oamenii de știință au înțeles gravitația descriind forța ca o deformare a țesăturii spațiului și timpului.”este încă uimitor pentru mine că o astfel de ecuație matematică poate descrie ce înseamnă spațiu-timp”, a declarat astrofizicianul Mario Livio de la Space Telescope Science Institute, care a nominalizat ecuația drept favorita sa. „Tot geniul adevărat al lui Einstein este întruchipat în această ecuație.”

” partea dreaptă a acestei ecuații descrie conținutul energetic al universului nostru (inclusiv „energia întunecată” care propulsează accelerația cosmică actuală)”, a explicat Livio. „Partea stângă descrie geometria spațiului-timp. Egalitatea reflectă faptul că în relativitatea generală a lui Einstein, masa și energia determină geometria și, concomitent, curbura, care este o manifestare a ceea ce numim gravitație.”

„este o ecuație foarte elegantă”, a spus Kyle Cranmer, fizician la Universitatea din New York, adăugând că ecuația dezvăluie relația dintre spațiu-timp și materie și energie. „Această ecuație vă spune cum sunt legate — cum prezența soarelui deformează spațiul-timp, astfel încât pământul se mișcă în jurul său pe orbită etc. De asemenea, vă spune cum a evoluat universul de la Big Bang și prezice că ar trebui să existe găuri negre.”

modelul Standard

o altă teorie a fizicii, modelul standard descrie colecția de particule fundamentale despre care se crede în prezent că alcătuiesc universul nostru.

teoria poate fi încapsulată într-o ecuație principală numită modelul standard Lagrangian (numit după matematicianul și astronomul francez din secolul 18 Joseph Louis Lagrange), care a fost ales de fizicianul teoretic Lance Dixon de la SLAC National Accelerator Laboratory din California ca formulă preferată.”a descris cu succes toate particulele elementare și forțele pe care le — am observat în laborator până în prezent-cu excepția gravitației”, a declarat Dixon pentru LiveScience. „Aceasta include, desigur, bosonul Higgs(asemănător) recent descoperit, phi în formulă. Este pe deplin în concordanță cu mecanica cuantică și relativitatea specială.”teoria modelului standard nu a fost încă unită cu relativitatea generală, motiv pentru care nu poate descrie gravitația.

calcul

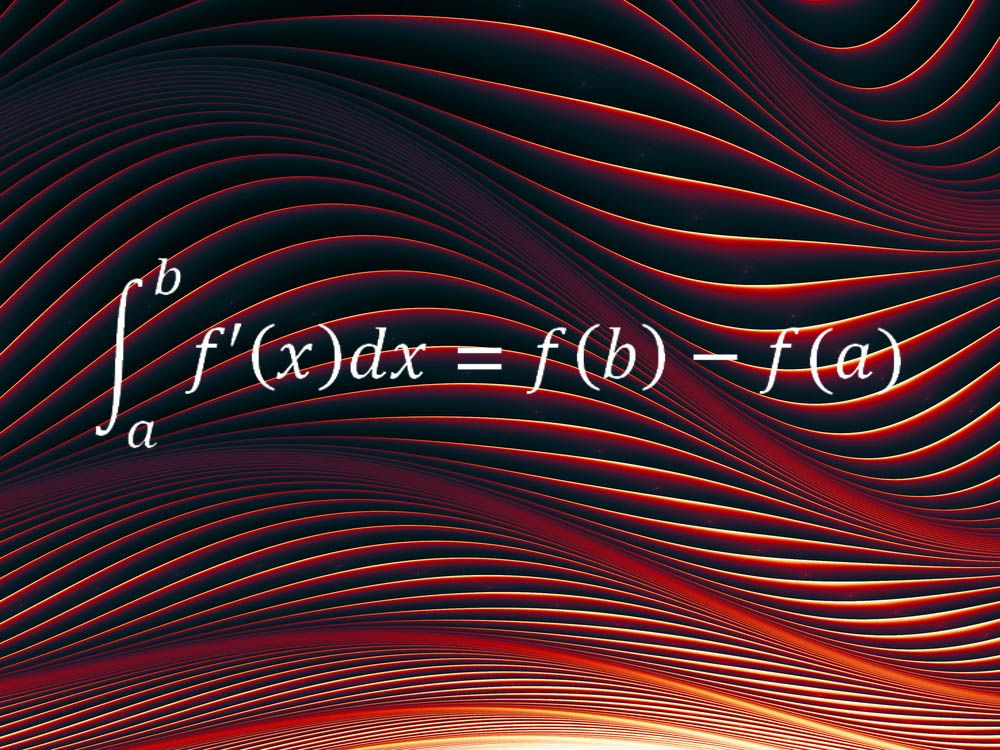
în timp ce primele două ecuații descriu aspecte particulare ale universului nostru, o altă ecuație preferată poate fi aplicată la tot felul de situații. Teorema fundamentală a calculului formează coloana vertebrală a metodei matematice cunoscută sub numele de calcul și leagă cele două idei principale ale sale, conceptul de integral și conceptul de derivat.

„în cuvinte simple, spune că schimbarea netă a unei cantități netede și continue, cum ar fi o distanță parcursă, într-un anumit interval de timp (adică. diferența dintre valorile cantității la punctele finale ale intervalului de timp) este egală cu integrala ratei de schimbare a acelei cantități, adică integrala vitezei”, a spus Melkana Brakalova-Trevithick, președinta Departamentului de matematică de la Universitatea Fordham, care a ales această ecuație ca favorită. „Teorema fundamentală a calculului (FTC) ne permite să determinăm schimbarea netă pe un interval pe baza ratei de schimbare pe întregul interval.”

semințele calculului au început în timpuri străvechi, dar o mare parte din ele au fost puse împreună în secolul al 17-lea de Isaac Newton, care a folosit calculul pentru a descrie mișcările planetelor din jurul Soarelui.

teorema lui Pitagora

o ecuație „veche, dar bună” este faimoasa teoremă pitagoreică, pe care fiecare student la geometrie începător o învață.

această formulă descrie modul în care, pentru orice triunghi cu unghi drept, pătratul lungimii ipotenuzei, c, (cea mai lungă latură a unui triunghi dreptunghiular) este egal cu suma pătratelor lungimilor celorlalte două laturi (a și b). Astfel, a^2 + b^2 = c^2

„primul fapt matematic care m-a uimit a fost teorema lui Pitagora”, a spus matematicianul Daina Taimina de la Universitatea Cornell. „Eram copil atunci și mi s-a părut atât de uimitor încât funcționează în geometrie și funcționează cu numere!”

1 = 0,999999999….

această ecuație simplă, care afirmă că cantitatea 0.999, urmată de un șir infinit de nouari, este echivalent cu unul, este favoritul matematicianului Steven strogatz de la Universitatea Cornell.”îmi place cât de simplu este — toată lumea înțelege ceea ce spune — dar cât de provocator este”, a spus Strogatz. „Mulți oameni nu cred că ar putea fi adevărat. Este, de asemenea, frumos echilibrat. Partea stângă reprezintă începutul matematicii; partea dreaptă reprezintă misterele Infinitului.”

relativitatea specială

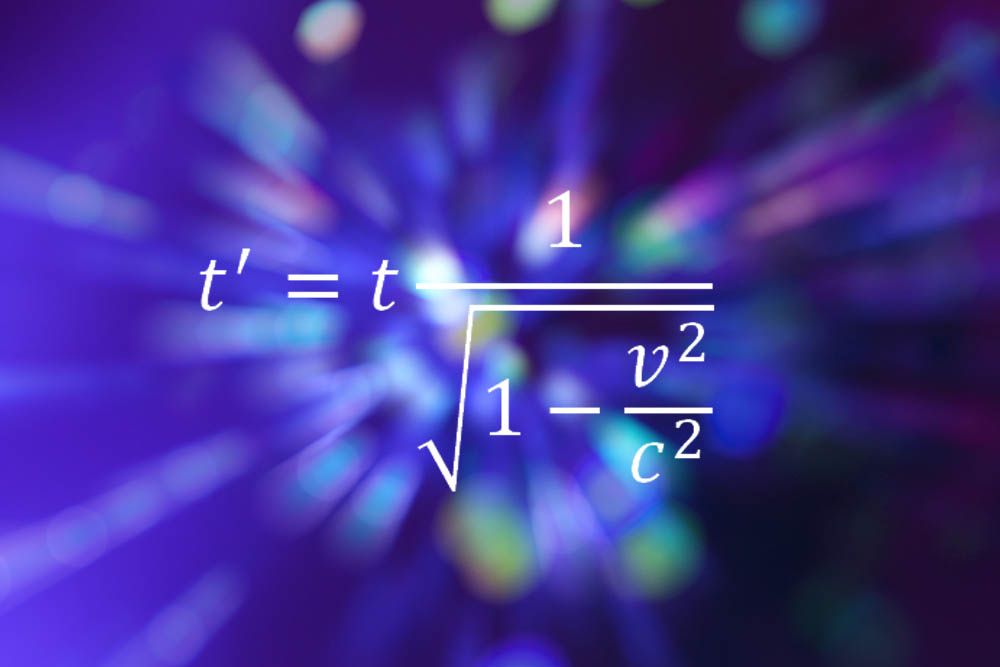
Einstein face din nou lista cu formulele sale pentru relativitatea specială, care descrie modul în care timpul și spațiul nu sunt concepte absolute, ci mai degrabă sunt relative în funcție de viteza observatorului. Ecuația de mai sus arată modul în care timpul se dilată sau încetinește, cu cât o persoană se mișcă mai repede în orice direcție.

„ideea este că este într-adevăr foarte simplu”, a spus Bill Murray, fizician de particule la laboratorul CERN din Geneva. „Nu există nimic acolo un student de nivel A nu poate face, nici derivate complexe și algebre urme. Dar ceea ce întruchipează este un mod cu totul nou de a privi lumea, o atitudine întreagă față de realitate și relația noastră cu ea. Dintr-o dată, cosmosul rigid neschimbat este măturat și înlocuit cu o lume personală, legată de ceea ce observați. Treceți de la a fi în afara universului, privind în jos, la una dintre componentele din interiorul acestuia. Dar conceptele și matematica pot fi înțelese de oricine dorește.”

Murray a spus că preferă ecuațiile relativității speciale în locul formulelor mai complicate din teoria ulterioară a lui Einstein. „Nu aș putea niciodată să urmez matematica relativității generale”, a spus el.

ecuația lui Euler

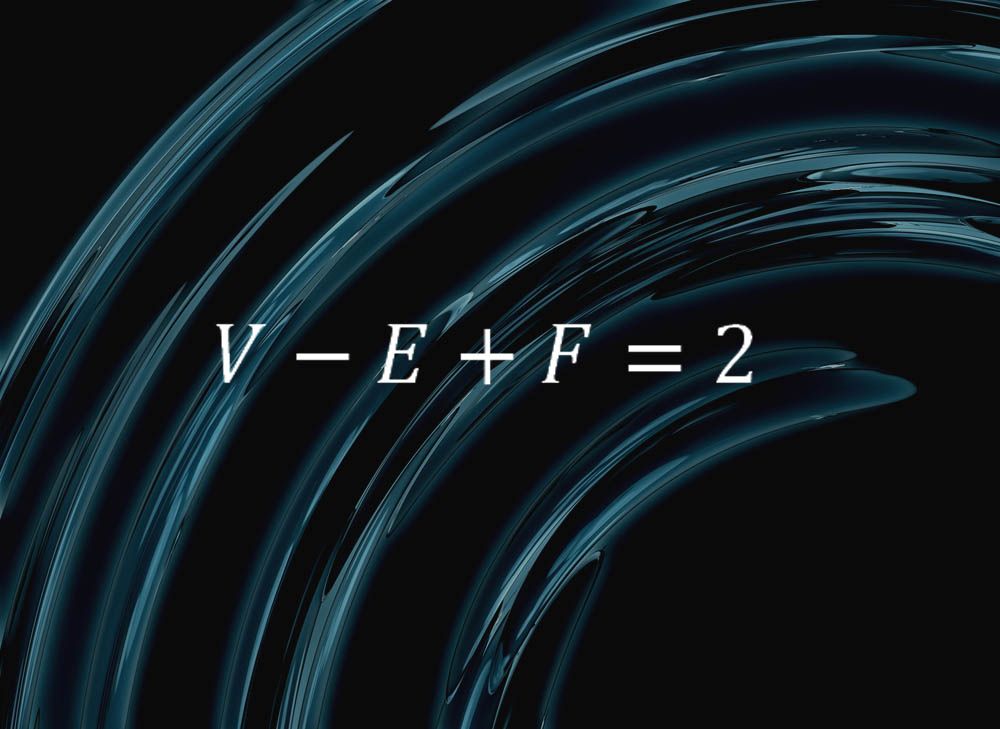
această formulă simplă încapsulează ceva pur despre natura sferelor:

„se spune că dacă tăiați suprafața unei sfere în fețe, margini și vârfuri și lăsați F să fie numărul de fețe, e numărul de margini și V Numărul de vârfuri, veți obține întotdeauna V – E + F = 2″, a spus Colin Adams, matematician la Colegiul Williams din Massachusetts.”de exemplu, luați un tetraedru, format din patru triunghiuri, șase muchii și patru vârfuri”, a explicat Adams. „Dacă ai sufla tare într-un tetraedru cu fețe flexibile, l-ai putea rotunji într-o sferă, astfel încât, în acest sens, o sferă poate fi tăiată în patru fețe, șase margini și patru vârfuri. Și vedem că V-e + F = 2. Același lucru este valabil și pentru o piramidă cu cinci fețe-patru triunghiulare și un pătrat — opt margini și cinci vârfuri” și orice altă combinație de fețe, margini și vârfuri.

„un fapt foarte cool! Combinatorica vârfurilor, marginilor și fețelor surprinde ceva foarte fundamental despre forma unei sfere”, a spus Adams.

ecuațiile Euler-Lagrange și teorema lui Noether

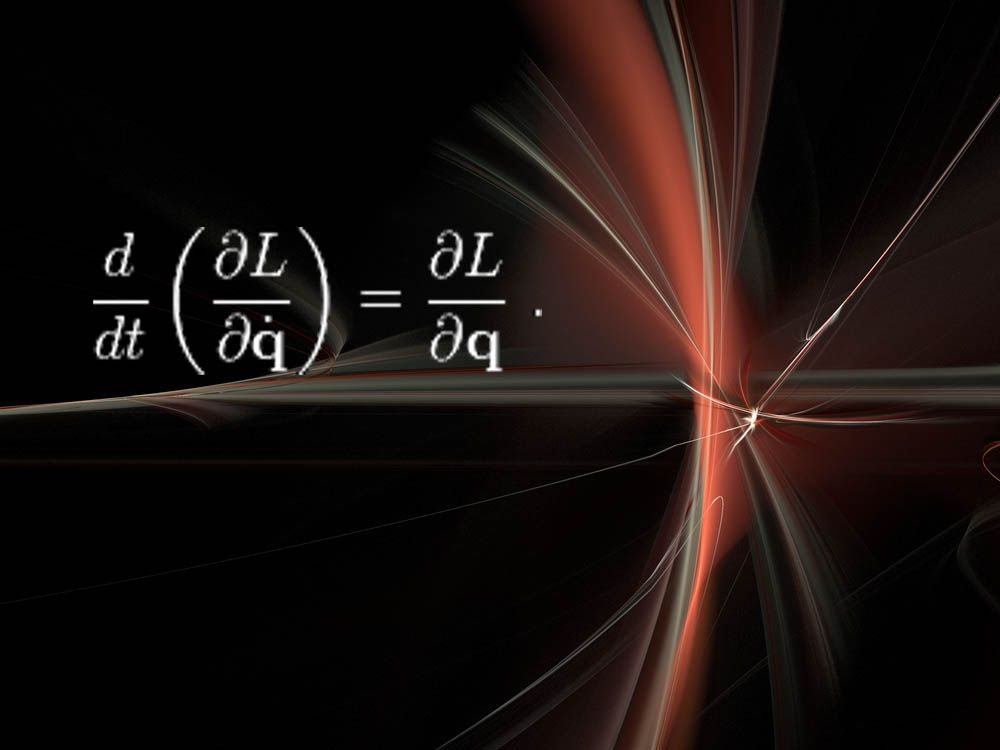
„acestea sunt destul de abstracte, dar uimitor de puternice”, a spus Cranmer de la NYU. „Interesant este că acest mod de gândire despre fizică a supraviețuit unor revoluții majore în fizică, cum ar fi mecanica cuantică, relativitatea etc.”

aici, L reprezintă Lagrangianul, care este o măsură a energiei într-un sistem fizic, cum ar fi izvoarele, pârghiile sau particulele fundamentale. „Rezolvarea acestei ecuații vă spune cum va evolua sistemul cu timpul”, a spus Cranmer.un spinoff al ecuației Lagrangiene se numește teorema lui Noether, după matematicianul German Emmy Noether din secolul 20. „Această teoremă este cu adevărat fundamentală pentru Fizică și rolul simetriei”, a spus Cranmer. „Informal, teorema este că, dacă sistemul dvs. are o simetrie, atunci există o lege de conservare corespunzătoare. De exemplu, ideea că legile fundamentale ale fizicii sunt aceleași astăzi ca mâine (simetria timpului) implică faptul că energia este conservată. Ideea că legile fizicii sunt aceleași aici ca și în spațiul cosmic implică faptul că impulsul este conservat. Simetria este probabil conceptul de conducere în fizica fundamentală, în primul rând datorită contribuției.”

ecuația Callan-Symanzik

„The Callan-ecuația symanzik este o ecuație vitală a primelor principii din 1970, esențială pentru a descrie modul în care așteptările naive vor eșua într-o lume cuantică”, a declarat fizicianul teoretic Matt strassler de la Universitatea Rutgers.ecuația are numeroase aplicații, inclusiv permițând Fizicienilor să estimeze masa și dimensiunea protonului și neutronului, care alcătuiesc nucleele atomilor.

fizica de bază ne spune că forța gravitațională și forța electrică dintre două obiecte sunt proporționale cu inversul distanței dintre ele pătrate. La un nivel simplu, același lucru este valabil și pentru forța nucleară puternică care leagă protonii și neutronii împreună pentru a forma nucleele atomilor și care leagă quarcii împreună pentru a forma protoni și neutroni. Cu toate acestea, fluctuațiile cuantice mici pot modifica ușor dependența unei forțe de distanță, ceea ce are consecințe dramatice pentru forța nucleară puternică.”împiedică această forță să scadă la distanțe mari și o face să prindă quarcii și să-i combine pentru a forma protonii și neutronii lumii noastre”, a spus Strassler. „Ceea ce face ecuația Callan-Symanzik este să coreleze acest efect dramatic și dificil de calculat, important atunci când este aproximativ dimensiunea unui proton, cu efecte mai subtile, dar mai ușor de calculat, care pot fi măsurate atunci când sunt mult mai mici decât un proton.”

ecuația suprafeței minime

” ecuația suprafeței minime codifică cumva frumoasele filme de săpun care formează pe limitele de sârmă atunci când le scufundați în apă cu săpun”, a spus matematicianul Frank Morgan de la Colegiul Williams. Faptul că ecuația este „neliniară”, care implică puteri și produse derivate, este indiciul matematic codificat pentru comportamentul surprinzător al filmelor de săpun. Acest lucru este în contrast cu ecuații diferențiale parțiale liniare mai familiare, cum ar fi ecuația căldurii, ecuația undelor, si ecuația Schr a fizicii cuantice.”