Cele mai frumoase și importante ecuații matematice
matematica este mai mult un maraton decât un sprint — este o măcinare lungă, lentă și constantă, cu momente rare de descoperire. Totuși, din când în când, obținem acele momente „Eureka” apreciate, acele linii scurte de Litere și numere care schimbă știința pentru totdeauna. Iată câteva dintre cele mai faimoase ecuații, de la grecii antici la fizica modernă.
Teorema lui Pitagora (530 î. HR.)
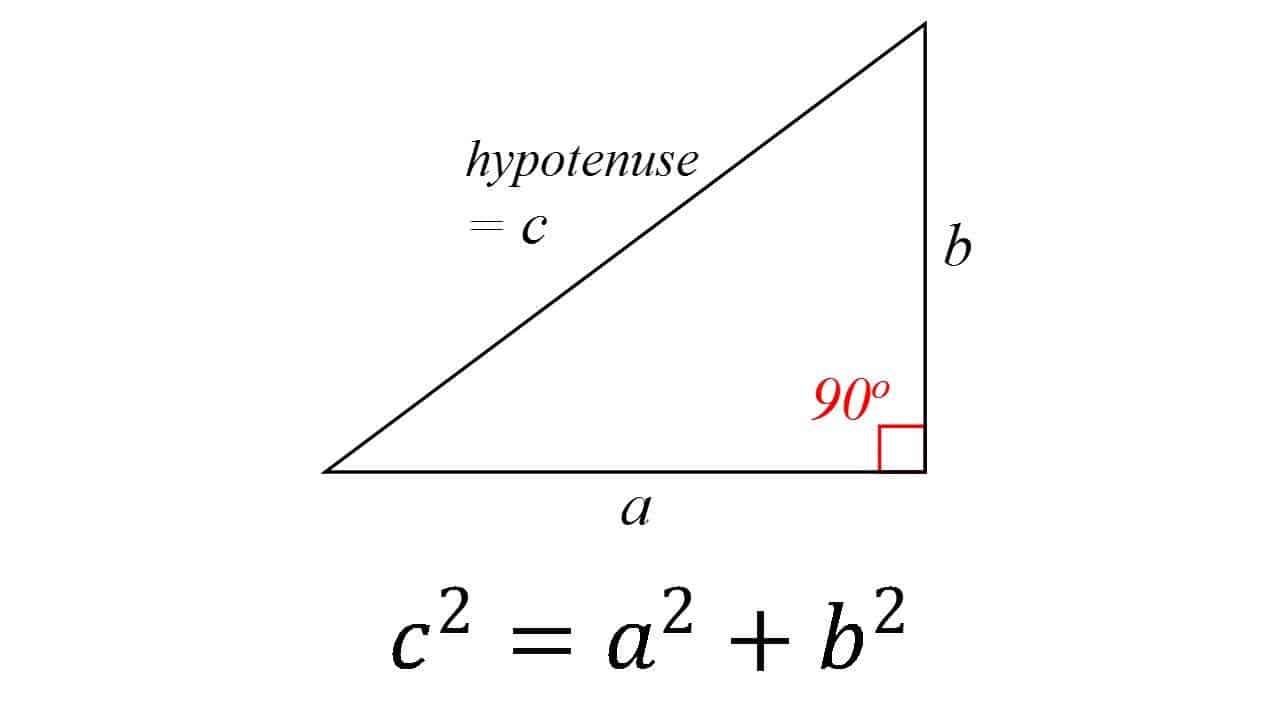
acesta este destul de unul dintre pilonii de bază toate geometrie: într-un triunghi drept, pătratul hipotenuzei (partea opusă unghiului drept) este egal cu suma pătratelor celorlalte două. Teoria este în general atribuită matematicianului Grec Pitagora, deși există unele dovezi că matematicienii babilonieni au înțeles formula. De asemenea, este foarte posibil ca teorema să fi fost cunoscută de mulți oameni, dar el a fost primul care a dovedit-o.teorema a primit numeroase dovezi-probabil cele mai multe pentru orice teoremă matematică. Sunt foarte diverse, incluzând atât dovezi geometrice, cât și dovezi algebrice, unele datând de mii de ani.
numere complexe

matematicianul italian Gerolamo Cardano este primul cunoscut care a introdus numere complexe, numindu-le „fictive” la acea vreme. Cu toate acestea, dezvoltarea matematică a „i” ca număr imaginar reprezentând rădăcina pătrată a lui -1 este atribuită lui Leonhard Euler, unul dintre cei mai importanți matematicieni și oameni de știință din istoria omenirii.
numerele complexe sunt practic numere care nu există cu adevărat, dar care sunt foarte utile pentru o serie de calcule. Ele constau din numere cu o parte reală (numerele pe care le cunoaștem cu toții) și o parte imaginară (eu reprezentată aici) și au aplicații practice în multe domenii, inclusiv fizică, chimie, biologie, economie, inginerie electrică și Statistică.
logaritmii

logaritmii sunt practic funcția inversă a exponențierii. Ai nevoie de un număr (N), o bază (a), iar logaritmul lui N în baza a va fi x, unde N este egal cu A cu puterea lui x. ar putea părea doar un mod diferit de a scrie același lucru (și într-un sens, este), dar logaritmii au o multitudine de aplicații practice, fiind folosiți în psihologie, economie și măsurători ale multor fenomene fizice (cum ar fi pH-ul sau magnitudinea cutremurului).
logaritmii au fost propuși public de John Napier în 1614, într — o carte intitulată Mirifici Logarithmorum Canonis Descriptio (descrierea minunatei reguli a logaritmilor) – un titlu potrivit. Un caz special de logaritm este logaritmul natural-e, unde e este un număr irațional și transcendental aproximativ egal cu 2.71828182845. De fapt, e în sine are o istorie fascinantă și un număr impresionant de aplicații, dar aceasta este o poveste pentru altă dată.
calculul
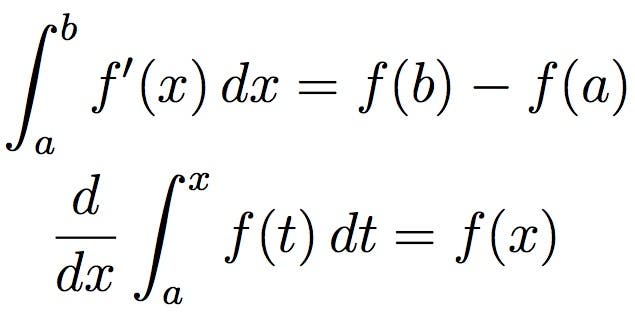
puține domenii ale matematicii au fost la fel de impactante ca calculul. Dezvoltat în secolul al 17-lea de Isaac Newton și Gottfried Wilhelm Leibniz, calculul este utilizat pe scară largă în știință, inginerie și economie. Calculul se concentrează de obicei pe tratarea cantităților mici, în special a cantităților infinit de mici. Prin calcul, acestea pot fi tratate ca numere reale, chiar dacă sunt infinit de mici din punct de vedere tehnic.
pentru o vizualizare mai simplă, integrarea, descrisă mai sus, poate fi considerată ca măsurând aria de sub o curbă, definită de o funcție.
legea gravitației
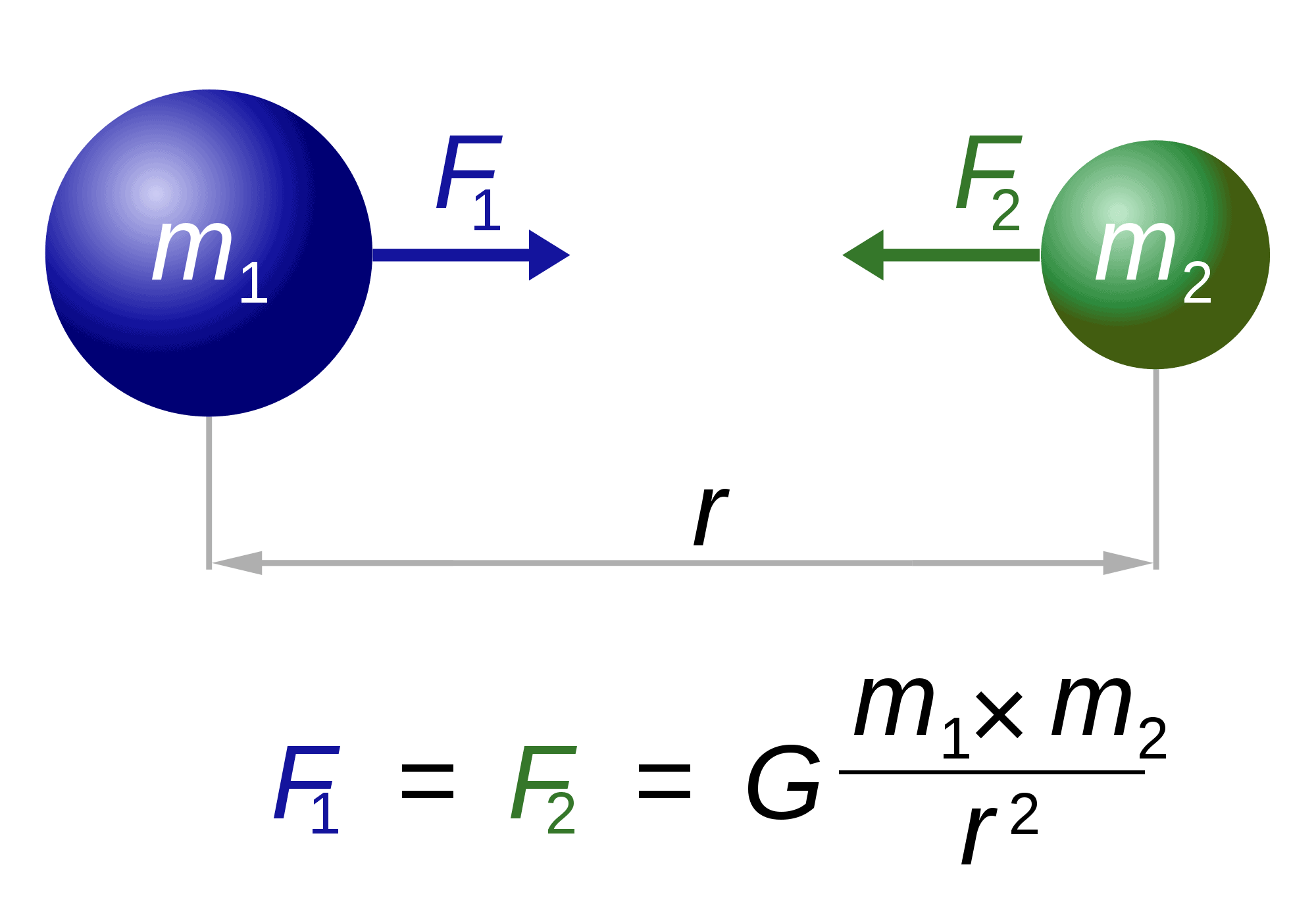
vorbind despre Newton, el este, de asemenea, „responsabil” pentru una dintre cele mai faimoase și spectaculoase ecuații din lume: legea gravitației.legea descrie practic modul în care oricare două corpuri de mase m1 și m2 sunt atrase unul de celălalt. Forța (F1, F2) este invers proporțională cu pătratul distanței dintre ele (r). Singurul factor rămas, G, este o constantă gravitațională. Natura acestei constante rămâne evazivă.
relativitatea generală

timp de aproape 200 de ani, legea lui Newton a definit nivelul nostru de înțelegere a mecanicii. Munca lui Einstein în secolul 20 a dus lucrurile la nivelul următor — aceste două realizări se află pe cele mai înalte piedestale din lumea fizicii.relativitatea generală este în esență o teorie geometrică a gravitației, generalizând teoria lui Newton oferind o descriere unificată a gravitației ca proprietate geometrică a spațiului și timpului — sau spațiu-timp. În special, Einstein a arătat nu numai că există un astfel de lucru ca „spațiu-timp” care îmbină cele trei dimensiuni cu dimensiunea a 4-a a timpului, dar a arătat, de asemenea, că acest spațiu-timp poate fi curbat de gravitație, curbura fiind direct legată de energia și impulsul oricărei materii și radiații sunt prezente.
A doua lege a termodinamicii
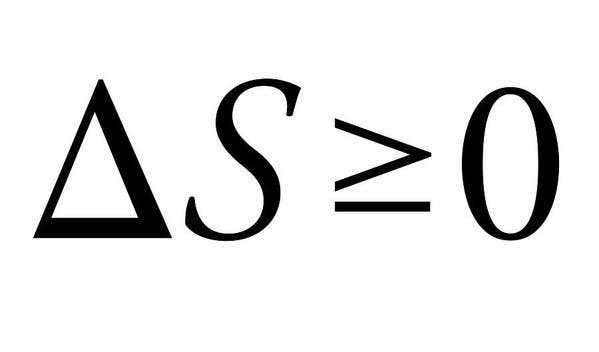
a doua lege a termodinamicii este motivul pentru care nu putem avea lucruri frumoase în univers. Lăsând glumele deoparte, cele patru legi ale termodinamicii definesc cantități fizice fundamentale (temperatură, energie și entropie) care caracterizează sistemele termodinamice. Al doilea, în special, se remarcă aici datorită simplității sale, dar implicațiilor absolut masive.
legea afirmă în esență că suma entropiilor sistemelor termodinamice care interacționează trebuie să crească întotdeauna sau cel mult să rămână constantă. Când energia se schimbă de la o formă la alta sau materia se mișcă, entropia (sau tulburarea) într-un sistem închis crește. Toate diferențele de temperatură, presiune și densitate tind să se aplatizeze după un timp
ecuațiile lui Maxwell
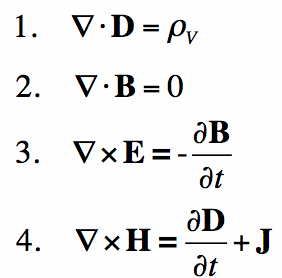
pur și simplu, ecuațiile lui Maxwell sunt pentru electromagnetism ceea ce legea lui Newton este pentru Mecanică. Ele oferă o bază matematică pentru electromagnetismul clasic, optica clasică și circuitele electrice. Sunt utilizate pe scară largă chiar în dispozitivul pe care citiți acest lucru — practic, toate dispozitivele electronice.legile lui Maxwell descriu modul în care câmpurile electrice și magnetice sunt generate de sarcini, curenți și schimbări ale câmpurilor. O descoperire semnificativă a fost demonstrația că câmpurile electrice și magnetice se propagă cu viteza luminii.
identitatea lui Euler

În cele din urmă, aceasta este probabil cea mai elegantă ecuație, un lucru de o frumusețe Supremă, deoarece implică toate numerele „de bază”:
- 0, care este neutru pentru adunare și scădere;
- 1, Care este neutru pentru înmulțire și împărțire;
- e, care numărul lui Euler (vezi mai sus), baza logaritmilor naturali;
- i este unitatea imaginară (vezi mai sus); și
- XV este pi, raportul dintre circumferința unui cerc și diametrul său.
găsirea unei relații care unifică toate aceste numere nu este decât uluitoare și pare destul de puțin probabilă. Demonstrația nu este tocmai simplă, dar o puteți vedea aici.este potrivit ca profesorul de matematică de la Universitatea Stanford, Keith Devlin, să descrie ecuația, spunând că „ca un sonet shakespearian care surprinde însăși esența iubirii sau un tablou care scoate în evidență frumusețea formei umane, care este mult mai mult decât adânc în piele, ecuația lui Euler ajunge până în adâncurile existenței”
nu este adesea că matematica și Fizica se aruncă la ecuații simple și elegante — dar atunci când o fac, este destul de o priveliște de privit.
Leave a Reply