beanz Magazine
harta lui Merian-Erben (1652) pe Wikipedia
puzzle-ul matematic din această lună datează din 1735 când a fost rezolvat pentru prima dată de Leonhard Euler, un matematician și fizician elvețian.
puzzle-ul se numește cele șapte poduri ale lui K. Nigsberg. Se bazează pe un oraș real, apoi în Prusia, acum Kaliningrad în Rusia. Orașul este împărțit de un râu cu două insule între ele și, mai în aval, râul împarte din nou orașul.
problema este inselator de simpla: există (sau erau, pe vremea lui Euler) șapte poduri pentru a conecta cele două insule și părțile din aval ale orașului. Euler s-a întrebat dacă o persoană ar putea traversa fiecare dintre cele șapte poduri o singură dată pentru a atinge fiecare parte a orașului. A începe și a termina în același loc nu a fost o cerință.
Iată o hartă pe care o puteți folosi pentru a încerca să rezolvați problema pentru dvs.:
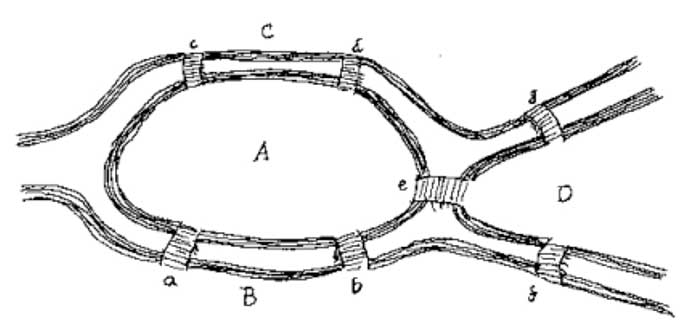
care credeți că este mai mult important pentru a rezolva această problemă: numărul de poduri sau locația fiecărui pod?
răspuns: Numărul de poduri.
Euler a dovedit că numărul de poduri trebuie să fie un număr par, de exemplu, șase poduri în loc de șapte, dacă doriți să mergeți peste fiecare pod o dată și să călătoriți în fiecare parte a k-ului. Soluția vede fiecare pod ca un punct final, un vârf în termeni matematici și conexiunile dintre fiecare pod (vârf). Euler și-a dat seama că doar un număr par de Poduri a dat rezultatul corect de a putea atinge fiecare parte a orașului fără a traversa un pod de două ori.Euler a folosit matematica pentru a dovedi că era imposibil să traverseze toate cele șapte poduri o singură dată și să viziteze fiecare parte a k-ului. Procedând astfel, el a pus în mișcare o serie de descoperiri și perspective despre modul în care spațiul și spațiile care se intersectează pot fi definite, precum și proprietățile lor. O descriere detaliată a soluției lui Euler în link-ul Wikipedia de mai jos acest articol.
dacă ați văzut vreodată o bandă mobius, de exemplu, ați văzut un exemplu de topologie, un domeniu matematic de studiu a evoluat din soluția lui Euler la această problemă. Topologia se referă la spațiu și la modul în care lucrurile se conectează unul la altul, precum și la continuitatea și limitele spațiului. Topologia studiază, de asemenea, modul în care proprietățile unui spațiu se schimbă și nu se schimbă atunci când spațiul este extins sau contractat.
în calcul, topologia este utilă în înțelegerea rețelelor (căilor) de date care pot curge în orice sistem, precum și a modului în care seturile de date se pot relaționa între ele. Cele șapte poduri de K, de asemenea, este similar cu o altă problemă comună de calcul numit uneori problema comis-voiajor în cazul în care încercați să găsiți cea mai eficientă rută dat un set de restricții, cum ar fi cele șapte poduri în problema lui Euler.
Non-matematicienii (probabil tu, cu siguranță eu) experimentează problema vânzătorului călător de fiecare dată când urcăm într-un tren sau autobuz. Problema comis-voiajor este imaginind cel mai eficient mod de a călători între perechi de orașe de distanțe specificate. Gestionarea resurselor limitate (trenuri, autobuze) care călătoresc de-a lungul rutelor finite este o problemă perfectă pentru rezolvarea calculelor, deoarece computerele sunt mai rapide și mai eficiente. Dar mai întâi avem nevoie de Euler și de alții pentru a afirma problema și a defini soluții cu matematica. Apoi programăm computerele noastre pentru a face matematica.
topologia se ocupă și de teoria mulțimilor, cum grupurile de lucruri pot fi sortate în seturi pentru a identifica elemente comune cu alte grupuri, precum și elemente unice. O diagramă Venn este un exemplu excelent de set. Și programarea uneori trebuie să sorteze datele în moduri diferite. Ce metodă de sortare funcționează cel mai bine pentru o situație poate fi determinată de teoria mulțimilor.și ce s-a întâmplat cu cele șapte poduri din vremea lui Euler? Două poduri au fost demolate și înlocuite cu o singură autostradă. Dintre cele trei poduri rămase, unul a fost reconstruit în 1935, în timp ce celelalte două rămân intacte, așa cum le cunoștea Euler. Și, desigur, K. Nigsberg, Prusia și-a schimbat numele în Kaliningrad, Rusia.
Leave a Reply