energetica formării legăturii ionice

legăturile ionice se formează atunci când ionii încărcați pozitiv și negativ sunt ținuți împreună de forțele electrostatice. Luați în considerare o singură pereche de ioni, un cation și un anion. Cât de puternică va fi forța atracției lor? Conform legii lui Coulomb, energia atracției electrostatice (\(E\)) între două particule încărcate este proporțională cu magnitudinea sarcinilor și invers proporțională cu distanța internucleară dintre particule (\(r\)):

\

\

unde sarcina fiecărui ion este reprezentată de simbolul Q. constanta de proporționalitate k este egală cu 2,31 xtc10-28 J·m. această valoare a lui k include sarcina unui singur electron (1,6022 xtc10-19 C) pentru fiecare ion. Ecuația poate fi scrisă și folosind sarcina fiecărui ion, exprimată în coulombi (C), încorporată în constantă. În acest caz, constanta de proporționalitate, k, este egală cu 8.999 XTX 109 J·m/C2. În exemplul dat, Q1 = + 1(1.6022 Int.10-19 C) și Q2 = -1(1.6022 Int. 10-19 c). Dacă Q1 și Q2 au semne opuse (ca în NaCl, de exemplu, unde Q1 este +1 Pentru Na+ și Q2 este -1 pentru Cl−), atunci E este negativ, ceea ce înseamnă că energia este eliberată atunci când ionii încărcați opus sunt aduși împreună de la o distanță infinită pentru a forma o pereche de ioni izolați.

energia este întotdeauna eliberată atunci când se formează o legătură și, în consecință, necesită întotdeauna energie pentru a rupe o legătură.

după cum arată curba verde din jumătatea inferioară a figurii \(\PageIndex{1}\), energia maximă ar fi eliberată atunci când ionii sunt infinit apropiați unul de celălalt, la r = 0. Deoarece ionii ocupă spațiu și au o structură cu nucleul pozitiv fiind înconjurat de electroni, cu toate acestea, ei nu pot fi infinit apropiați. La distanțe foarte scurte, interacțiunile electron–electron respingătoare dintre electronii de pe ionii adiacenți devin mai puternice decât interacțiunile atractive dintre ionii cu sarcini opuse, așa cum arată curba roșie din jumătatea superioară a figurii \(\PageIndex{1}\). Energia totală a sistemului este un echilibru între interacțiunile atractive și respingătoare. Curba purpurie din Figura \(\PageIndex{1}\) arată că energia totală a sistemului atinge un minim la r0, punctul în care repulsiile și atracțiile electrostatice sunt exact echilibrate. Această distanță este aceeași cu Distanța de legătură măsurată experimental.

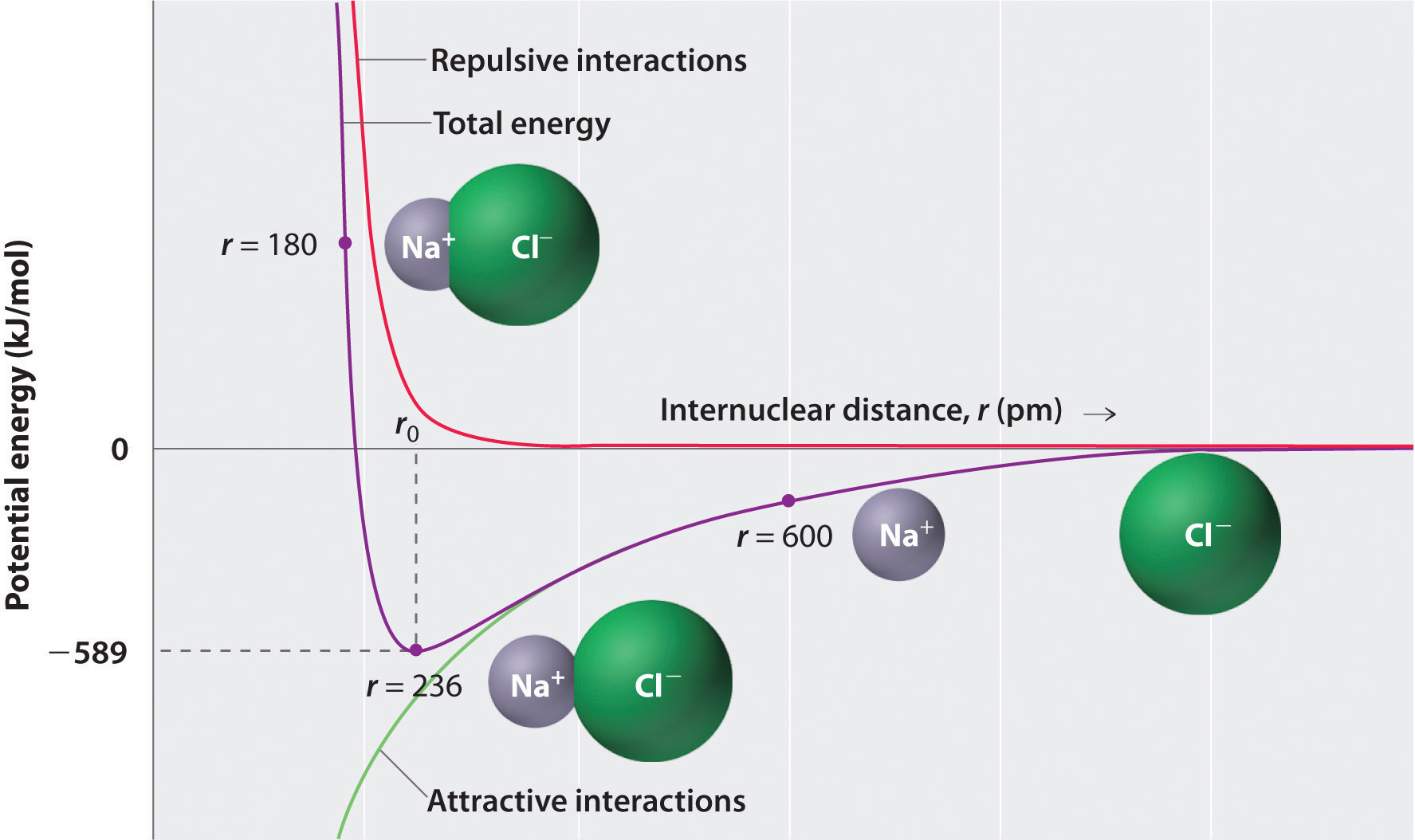
luați în considerare energia eliberată atunci când un ion gazos \(Na^+\) și un ion gazos \(Cl^-\) sunt aduși împreună de la r = Irak la r = r0. Având în vedere că distanța internucleară observată în fază gazoasă este de 236 pm, schimbarea de energie asociată cu formarea unei perechi de ioni dintr-un ion \(Na^+_{(g)}\) și un ion \(Cl^-_{(g)}\) este după cum urmează:

\ &= (2,31 \times {10^{ – 28}}\rm{J}\cdot \cancel{m} ) \stânga( \dfrac{( + 1)( – 1)}{236\; \anulează{pm} \ ori 10 ^ {- 12} \ anulează{m / pm}} \dreapta) \ \ & = – 9.79 \ times 10 ^ {- 19}\; J / ion\; pereche \ label{Eq2} \ end{align*}\]

valoarea negativă indică faptul că energia este eliberată. Convenția noastră este că, dacă un proces chimic furnizează energie lumii exterioare, schimbarea energiei este negativă. Dacă este nevoie de energie, schimbarea energiei este pozitivă. Pentru a calcula schimbarea energiei în formarea unui mol de perechi de NaCl, trebuie să înmulțim energia per pereche de ioni cu numărul lui Avogadro:

\

aceasta este energia eliberată atunci când se formează 1 mol de perechi de ioni gazoși, nu atunci când 1 mol de ioni pozitivi și negativi se condensează pentru a forma o rețea cristalină. Datorită interacțiunilor pe distanțe lungi în structura rețelei, această energie nu corespunde direct cu energia rețelei solidului cristalin. Cu toate acestea, valoarea negativă mare indică faptul că reunirea ionilor pozitivi și negativi este foarte favorabilă din punct de vedere energetic, indiferent dacă se formează o pereche de ioni sau o rețea cristalină.

rezumăm punctele importante despre legătura ionică:

• la r0, ionii sunt mai stabili (au o energie potențială mai mică) decât sunt la o distanță internucleară infinită. Atunci când ionii încărcați opus sunt aduși împreună de la r = XV la r = r0, energia sistemului este redusă (energia este eliberată).
• din cauza energiei potențiale scăzute la r0, energia trebuie adăugată în sistem pentru a separa ionii. Cantitatea de energie necesară este energia legăturii.
• energia sistemului atinge un minim la o anumită distanță internucleară (distanța de legătură).