Seqüência de Fibonacci
A Sequência de Fibonacci é a série de números:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
O próximo número é encontrado somando-se os dois números antes:
- 2 é encontrado pela adição de dois números antes de (1+1),
- o 3 é encontrado pela adição de dois números antes de (1+2),
- 5 (2+3),
- e assim por diante!
exemplo: o próximo número na sequência acima é 21+34 = 55
É assim tão simples!
Aqui está uma lista maior:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …pode descobrir os próximos números?
faz uma espiral
quando fazemos quadrados com essas larguras, temos uma boa espiral:
por exemplo, 5 e 8 fazem 13, 8 e 13 fazem 21, e assim por diante.

esta espiral é encontrada na natureza!
See: Nature,the Golden Ratio, and Fibonacci
The Rule
The Fibonacci Sequence can be written as a “Rule” (see Sequences and Series).em primeiro lugar, os termos são numerados a partir de 0 em diante.:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
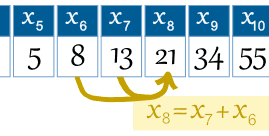
Então, prazo, número 6 é chamado x6 (que é igual a 8).
|
Exemplo: 8º termo é x8 = x7 + x6 |
 |
Então, podemos escrever a regra:
A Regra é xn = xn−1 + xn−2
onde:
- xn é termo de número “n”
- xn−1 é o termo anterior (n−1)
- xn−2 é o termo antes que (n−2)
Exemplo: termo 9 é calculado assim:
Rácio de Ouro
E aqui é uma surpresa. Quando tomamos dois números sucessivos (um após o outro) de Fibonacci, sua razão é muito próxima à razão dourada “φ” Que é aproximadamente 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
não temos que iniciar com 2 e 3, aqui me escolheu aleatoriamente 192 e 16 (e tenho a sequência 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
demora mais para obter bons valores, mas mostra que não só a sequência de Fibonacci pode fazer isso!
Usando A Razão Áurea para Calcular os Números de Fibonacci
E ainda mais surpreendente é que podemos calcular qualquer Número de Fibonacci usando a Razão Áurea:
xn = φn − (1−φ)n√5
A resposta vem como um número inteiro, exatamente igual, a adição dos dois termos.
exemplo: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
Quando eu usei uma calculadora sobre isso (apenas entrando na razão de ouro para 6 casas decimais) eu recebi a resposta 8.00000033 , um cálculo mais preciso seria mais próximo de 8.
tente n = 12 e veja o que tem.
Pode também calcular um número de Fibonacci multiplicando o número anterior de Fibonacci pela razão dourada e arredondando em seguida (obras para números acima de 1):
exemplo: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (arredondado)
algumas coisas interessantes
Aqui está a sequência de Fibonacci novamente:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
Há um padrão interessante:
- Olhar para o número x3 = 2. Cada terceiro número é um múltiplo de 2 (2, 8, 34, 144, 610, …)
- Olhe para o número x4 = 3. Cada quarto número é um múltiplo de 3 (3, 21, 144,…)
- Olhe para o número x5 = 5. Cada quinto número é um múltiplo de 5 (5, 55, 610,…)
e assim por diante (cada n-ésimo número é um múltiplo de xn).
1/89 = 0, 011235955056179775…Nota: os primeiros dígitos (0,1,1, 2,3,5) são a sequência de Fibonacci?
In a way they all are, except multiple digit numbers (13, 21, etc) sobreposição, like this:
.. etc …
0, 011235955056179775… = 1/89
Termos Abaixo de Zero
funciona A sequência abaixo de zero também, como este:
| n = | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(Provar para si mesmo que cada número é encontrado somando-se os dois números antes!)
Na verdade, a sequência abaixo de zero tem os mesmos números que a sequência acima de zero, exceto que eles seguem um+ -+ -… padrao. Ele pode ser escrito desta forma:
x−n = (-1)n+1 xn
que diz que o termo “n” é igual a (-1)n+1 vezes o termo “n”, e o valor (-1)n+1 ordenadamente faz o correto +1, -1, +1, -1, … padrao.
história
Fibonacci não foi o primeiro a saber sobre a sequência, foi conhecido na Índia centenas de anos antes!

Sobre Fibonacci O Homem
Seu verdadeiro nome era Leonardo Pisano Bogollo, e ele viveu entre 1170 e 1250, na Itália.
“Fibonacci” era o seu apelido, que significa “filho de Bonacci”.além de ser famoso pela sequência de Fibonacci, ele ajudou a espalhar Numerais Hindu-árabes (como os nossos números atuais 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) através da Europa, em vez dos algarismos Romanos (I, II, III, IV, V, etc.). Isso salvou-nos a todos um monte de problemas! Obrigado Leonardo.

Fibonacci Dia
Fibonacci Dia 23 de novembro, como tem os números “1, 1, 2, 3”, que é parte da seqüência. Por isso no próximo 23 de Novembro avisa toda a gente!


Leave a Reply