o grafo de uma desigualdade linear em uma variável é uma linha de números. Use um círculo aberto para < e > e um círculo fechado para ≤ e ≥.

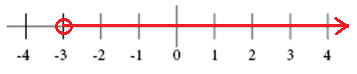
O gráfico para x > -3

O gráfico para x ≥ 2

as Desigualdades que têm a mesma solução são chamados de equivalentes. Há propriedades de desigualdades, bem como propriedades de igualdade. Todas as propriedades abaixo também são verdadeiras para desigualdades envolvendo ≥ e ≤.

A adição de propriedade da desigualdade diz que adicionar o mesmo número de cada lado da desigualdade produz um equivalente a desigualdade

$Se$\: x>y,\:, em seguida,\: x+z>y+z$$

$Se$\: x<y,\:, em seguida,\: x+z <y+z$

a propriedade de subtração da desigualdade nos diz que subtrair o mesmo número de ambos os lados de uma desigualdade dá uma desigualdade equivalente.

$Se$\: x>y,\:, em seguida,\: x-z>y-z$$

$Se$\: x<y,\:, em seguida,\: x-z<y-z$$

A multiplicação de propriedade da desigualdade nos diz que a multiplicação de ambos os lados de uma desigualdade com um número positivo produz um equivalente a desigualdade.

$$If \: x >y \: e\: z>0,\:, em seguida,\: xz>yz$$

$Se$\: x<y\: e\: z>0,\:, em seguida,\: xz<yz$$

a Multiplicação em cada lado de uma desigualdade com um número negativo, por outro lado, não produz um equivalente a desigualdade, a menos que nós também inverter a direção da desigualdade símbolo

$Se$\: x>y \: e\: z<0,\ :, em seguida,\: xz<yz$$

$Se$\: x<y\: e\: z <0,\: then\: xz>yz$

the same goes for the division property of inequality.

Divisão de ambos os lados de uma desigualdade com um número positivo produz uma desigualdade equivalente.

$Se$\: x>y \: e\: z>0,\:, em seguida,\: \frac{x}{z}>\frac{y}{z}$$

$Se$\: x<y\: e\: z>0,\:, em seguida,\: \frac{x}{z}<\frac{y}{z}$

e a divisão em ambos os lados de uma desigualdade com um número negativo produz uma desigualdade equivalente se o símbolo de desigualdade for revertido.

$Se$\: x>y \: e\: z<0,\:, em seguida,\: \frac{x}{z}<\frac{y}{z}$$

$Se$\: x<y\: e\: z<0,\:, em seguida,\: \frac{x}{z}>\frac{y}{z}$$

Para resolver um multi-passo a desigualdade de você fazer o que você fez quando a solução multi-passo equações. Tome uma coisa no momento, de preferência começando por isolar a variável das constantes. Ao resolver desigualdades em várias etapas é importante não esquecer de reverter o sinal de desigualdade ao multiplicar ou dividir com números negativos.

Exemplo

Resolver a desigualdade

$$-2\left ( x+3 \right )<10$$