Quadrados e Retangulares HSS-para-HSS Momento de Conexões
Por Jason McCormick
Professor Associado, Civil & Engenharia Ambiental, da Universidade de Michigan, Ann Arbor, MI, USA
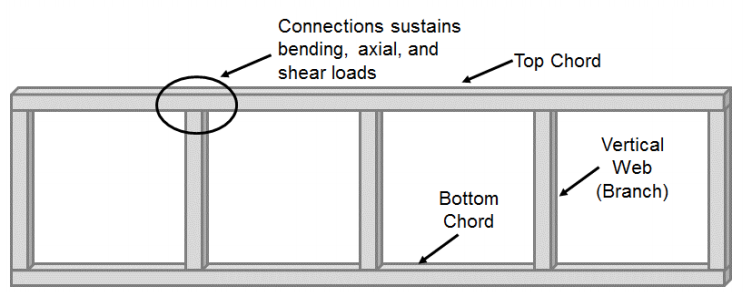
Momento ligações feitas de retangular e quadrado oco secções estruturais (HSS) têm recebido menos atenção comparado com HSS-para-HSS ligações feitas de axialmente carregado membros (T-, Y-, cruz-, e K-conexões). A maioria dos estudos estáticos focados nestas conexões têm considerado Sistemas de truss Vierendeel. Estes sistemas são muitas vezes formados por acordes quadrados ou retangulares superiores e inferiores que estão conectados com membros quadrados ou retangulares verticais (ramificação) (Figura 1). Como resultado desta configuração, a conexão corda-a-web passa por flexões significativas junto com cargas transversais e axiais e não é considerada uma conexão PIN como é comumente feito em sistemas truss típicos. Originalmente concebido em 1896 por Arthur Vierendeel, não foi até que HSS foram desenvolvidos que o potencial para trusses Vierendeel começou a ser realizado (Korol et al. 1977), mas o seu uso exigia uma compreensão de como transferir o momento entre as conexões T HSS-para-HSS.
Muitos dos primeiros estudos sobre essas conexões focada na capacidade da conexão para desenvolver a plena capacidade de momento da sucursal membro. Jubb e Redwood (1966) mostraram que, quando o ramo seção tinha uma largura igual ao acorde seção (β=1) a plena capacidade de momento da HSS-membro poderia ser alcançado sem reforço. No entanto, este estudo não considerou a potencial perda de capacidade momentânea devido à presença de carga axial. Por outro lado, Korol et al. (1977) mostrou que as ligações com um pequeno ramo de largura do que o acorde não se pode desenvolver a plena capacidade de momento da sucursal sem reforço, através de uma série de 29 de diferentes testes de conexão, considerando 5 configurações diferentes (não armado, ramo de flange reforço de placas, acorde flange de reforços, haunch, e tronco de pirâmide). Em geral, a força e a rigidez das ligações de tipo Vierendeel não reforçadas diminuem com um aumento na taxa de esbelteza de acordes (B/t) e uma diminuição na relação de largura de ramo / acorde (β). Como resultado, as ligações do tipo Vierendeel truss não encerradas só podem ser consideradas rígidas (isto é, sujeitas a uma rotação relativa mínima entre o acorde e o ramo) quando a relação de largura entre o ramo e o acorde é de 1,0 e a relação de relevo é baixa ou a ligação é reforçada (Packer 1993).dado que os momentos máximos destas articulações podem ocorrer em deformações excessivamente grandes, é adoptada uma abordagem semelhante à utilizada para juntas de HSS com carga axial quadrada e rectangular, em que por uma capacidade de rolamento final ou um limite de deformação ou rotação é utilizado para caracterizar o momento de projecto (Wardenier 1982). AISC 360-10 (Capítulo K3) considera três estados-limite para conexões T de HSS quadradas e Retangulares sob flexão estática em plano: plastificação de cordas, produção local de paredes laterais e produção local do ramo devido à distribuição desigual da carga. A plastificação da parede de acordes ocorre como resultado da largura do membro do ramo ser menor que a largura do acorde (β ≤ 0,85), exigindo que a tensão e as cargas de compressão produzidas pelo momento Flector sejam transferidas através da face relativamente flexível do acorde, em vez de diretamente para as paredes laterais mais duras. A equação do Estado Limite (AISC 360-10 equação K3-6) pode ser derivada da teoria da linha de rendimento (Figura 2):
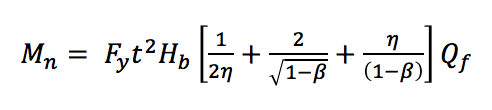
Mn é o valor nominal de capacidade de momento da ligação, Fy é o especificado força de rendimento mínimo de acorde, Hb é a altura total do ramo, h é a carga do parâmetro de comprimento igual à altura do ramo dividida pela largura do acorde (assumindo um ângulo de 90o entre a corda e o ramo de membro, como é típico de Vierendeel treliças)e Qf é um parâmetro para reduzir a capacidade de articulação em presença de compressão axial do acorde.
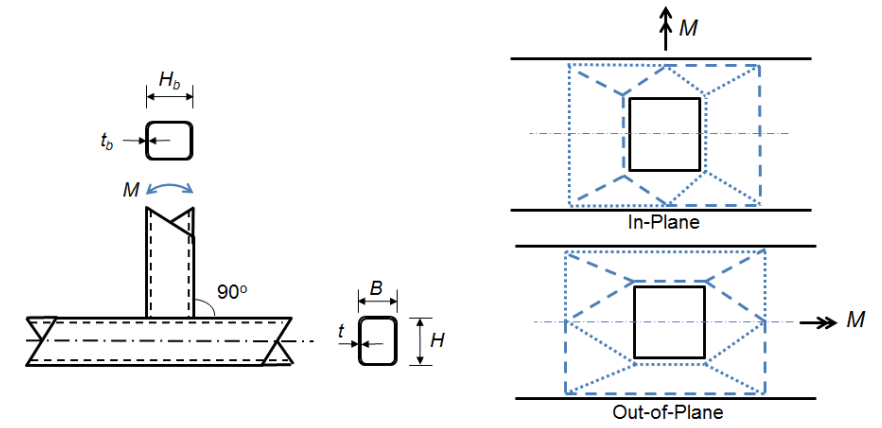
Os outros dois estados-limite estão associados com conexões onde a largura do ramo membro é igual ou quase igual à largura do acorde (β > 0.85) significando que as cargas de tensão e compressão desenvolvidas nas flanges do membro do ramo são transferidas quase diretamente para as laterais mais duras do acorde. O estado limite para o sidewall local de produção (AISC 360-10 Equação K3-7) de uma conexão em T, em seguida, pode ser derivada a partir da web local produzindo equação para concentrados de forças aplicadas a uma distância da extremidade do membro maior que sua profundidade (AISC 360-10 Equação J10-2):
Mn = 0.5Fyt(Hb + 5t)2
a Equação 2
Para o local de paragem do ramo, devido à desigual distribuição de carga (AISC 360-10 Equação K3-8) em uma conexão em T, uma largura efetiva abordagem é utilizada para reduzir a capacidade da órtese de membro para obter nominal momento aplicado pela cinta:
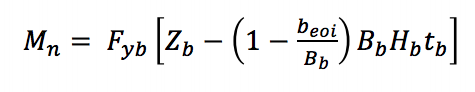
Fyb é o mínimo especificado força de rendimento do ramo, Zb é o módulo resistente plástico da sucursal sobre o eixo de flexão, beoi é a largura efetiva do ramo, o Bb é a largura total do ramo, e tb é o design da espessura de parede do ramo.
porque existe uma evidência experimental limitada para suportar modelos específicos de design para conexões de truss Vierendeel (conexões T) sob flexão fora do plano, Estados limite análogos como aqueles para flexão no plano são usados (Packer et al. 2010). Um estado-limite adicional de falha da distorção de acordes desenvolve-se a partir do binário aplicado ao acorde pelo membro do ramo como resultado do momento fora de plano. Este torque pode levar a distorção romboidal do acorde. As equações de momento nominal para flexão fora do plano podem ser encontradas nas equações de AISC 360-10 K3-9, K3-10, K3-11 e K3-12. As equações para a flexão em plano e fora de plano de conexões T são semelhantes às que foram adotadas internacionalmente (Packer et al. 2010).as equações de projeto acima foram derivadas considerando os sistemas de truss de Vierendeel sob cargas estáticas. Um estudo recente (Fadden et al. 2015) promoveu este trabalho para considerar o comportamento de conexões de momento quadrado e retangular HSS-a-HSS sob grandes cargas cíclicas para uso em sistemas de quadros de momento sísmico baseados em tubos (quadros de momento intermediários e especiais). Tal sistema parece aproveitar as excelentes propriedades axiais, dobradoras e torcionais, alta relação força-peso, e natureza arquitetonicamente agradável de quadrados e Retangulares HSS. A alta resistência à torção pode levar a uma redução do contravalor do feixe, enquanto a alta relação força-peso resulta em menor massa sísmica. No entanto, essas ligações devem poder ser submetidas a uma fixação de plástico estável do membro do feixe, em que 80% da capacidade de plástico do membro do feixe é mantida a 0,2 rad. (FMI) ou 0,4 rad. (SMF) of inter-story drift (AISC 341-10). Dado que o projeto sísmico atual dos sistemas de quadro de momento requer a maioria do comportamento inelástico para ocorrer no membro do feixe, o membro do feixe também deve atingir a sua capacidade plástica completa antes de passar por buckling local. Fadden e McCormick (2014a) considerados experimentais e modelos de elementos finitos para determinar a limitação de largura, espessura e profundidade, espessura requisitos para o HSS sob flexão desde aqueles especificados no atual AISC Sísmica Provisões (AISC 341-10) foram largamente desenvolvida com base em testes de cíclico carregado axialmente HSS membros.
para determinar a configuração adequada e detalhando os requisitos para atender a esta demanda de resistência e ductilidade, quatro configurações de conexão diferentes foram experimentalmente testadas: duas conexões não-forçadas soldadas diretamente (não compensadas e compensadas) e duas Conexões reforçadas (através de placa e placa de diafragma externa). Todas as conexões utilizaram uma coluna HSS 10x10x5/8. As conexões diretamente soldadas utilizavam soldagens CJP pré-qualificadas, conforme especificado em AWS D1. 1 (2010). Para a conexão inigualável, o feixe era um HSS 12x8x3 / 8 (β = 0.8) sugerindo que a plastificação da face da coluna pode ser uma preocupação. Para a conexão emparelhada, o feixe era um HSS 12x10x3/8 (β = 1.0) permitindo que as cargas fossem transferidas diretamente para a parede lateral. O protocolo de carga AISC para pré-qualificação de conexões de momento sísmico foi utilizado (AISC 341-10) para carregar as conexões. O comportamento das conexões foi como previsto com a conexão incomparável mostrando deformação na face da coluna, enquanto a conexão correspondida foi capaz de transferir a carga para as paredes laterais da coluna. No entanto, ambas as ligações falharam devido à fractura no metal base da coluna no dedo do pé do canto da soldadura (Figura 3). This quebradiço failure at rotations of 0.4 rad. e 0,5 rad., respectivamente, confirmou que as conexões soldadas diretamente não fornecem o comportamento apropriado para aplicações sísmicas.

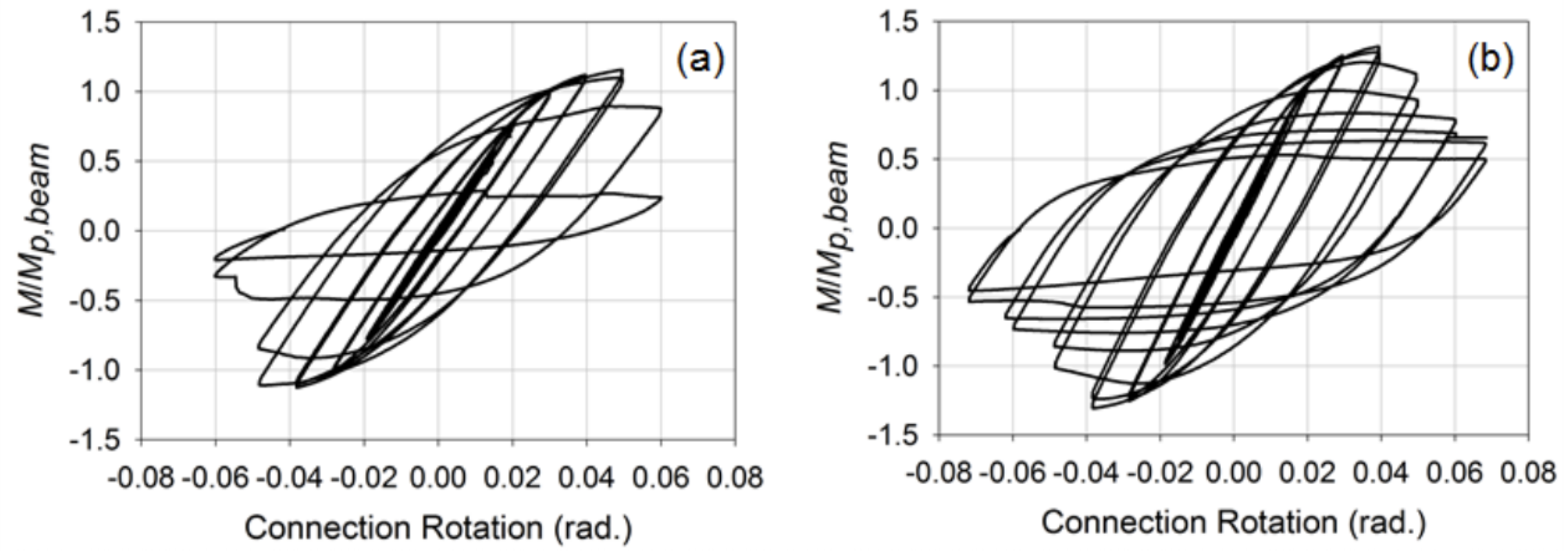
O reforço de ligações, em seguida, foram desenvolvidos considerando-se através da placa externos e diafragma de placas, que são muitas vezes utilizados em uma grande flange de feixe-de-HSS coluna conexões a fim de proporcionar um melhor mecanismo de transferência de tensão e compressão de forças para a parede lateral da coluna e minimizar as concentrações de tensão colocada em soldas. Para estas conexões, as vigas eram membros HSS 12x8x3/8 (β = 0.8). Informações relativas ao procedimento específico utilizado para conceber e detalhar estas ligações podem ser encontradas em Fadden e McCormick (2014b) e Fadden et al. (2015). Colocadas sob a mesma carga que as conexões não reforçadas, as conexões mostraram um comportamento mais estável com a dobradiça plástica ocorrendo longe da face da coluna na extremidade da placa de diafragma através Ou Externa (Figura 4). Ambas as conexões também foram capazes de alcançar 0,4 rad. de rotação antes de passar por um sistema de Fecho local que resultou na degradação da capacidade do momento. No entanto, a fratura começou no canto do feixe de HSS devido ao ciclismo em grandes níveis de rotação de 0,7 rad. Uma comparação das curvas normalizadas de rotação momentânea para as conexões de placas de diafragma emparelhadas e externas pode ser vista na Figura 5. No geral, as Conexões reforçadas mostraram promessa de uso de sistemas de momento sísmico de HSS-a-HSS, mas mais trabalho é necessário para mover essas conexões para uma eventual pré-qualificação.

AISC. (2010). “Sismic Provisions for Structural Steel Buildings”. ANSI / AISC 341-10. American Institute of Steel Construction, Chicago, IL.
AISC. (2010). “Specifications for Structural Steel Buildings”. ANSI / AISC 360-10. American Institute of Steel Construction, Chicago, IL.
AWS. (2010). “Código De Soldadura Estrutural”. ANSI / AWS D1. 1, American Welding Society, Miami, FL.
Fadden, F. and McCormick, J. (2014a). “Finite Element Model of the Cyclic Flexing Behavior of Hollow Structural Sections”. Journal of Constructional Steel Research, 94, 64-75.
Fadden, F. and McCormick, J. (2014b). “HSS-to-HSS Sismic Moment Connection Performance and Design”. Journal of Constructional Steel Research, 101, 373-384.Fadden, F., Wei, D., and McCormick, J. (2015). “Cyclic Testing of Welded HSS-to-HSS Moment Connections for Sismic Applications”. ASCE Journal of Structural Engineering, 141 (2), 04014109-1-14.Jubb, J. E. M. and Redwood, R. G. (1966). “Design of Joints to Box Sections”. The Institution of Structural Engineers, Conference on Industrialized Building and the Structural Engineer, Institute of Structural Engineers, London.Korol, R. M., El-Zanaty, M., and Brady, F. J. (1977). “Unequal Width Connections of Square Hollow Sections in Vierendeel Trusses”. Canadian Journal of Civil Engineering, 4, 190-201.
Packer, J. A. (1993). “Moment Connections between Rectangular Hollow Sections”. Journal of Constructional Steel Research, 25, 63-81.
Packer, J. A., Wardenier, J., Zhao, X. L., van der Vegte, G. J. and Kurobane, Y. (2010). Guia de projecto 3: para juntas rectangulares de Secção Oca (RHS) sob carga predominantemente estática 2.A edição. CIDECT, Canadá.
Wardenier, J. (1982). “Articulações Ocas”. Delft University Press, Delft, Holanda.
setembro 2016
Download PDF
Leave a Reply