eu sempre confundi “permutação” e “combinação” — Qual é qual?

Aqui está uma maneira fácil de lembrar: a permutação parece complicada, não é? E é. Com permutações, cada pequeno detalhe importa. Alice, Bob e Charlie são diferentes de Charlie, Bob e Alice (inserir os nomes de seus amigos aqui).combinações

, Por outro lado, são muito fáceis de seguir. Os detalhes não importam. Alice, Bob e Charlie são os mesmos que Charlie, Bob e Alice.

permutações são para listas (assuntos de ordem) e combinações são para grupos (ordem não importa).

Você sabe, um ” bloqueio de combinação “deveria ser chamado de”bloqueio de permutação”. A ordem em que pões os números em questão.

uma verdadeira “fechadura combinada” aceitaria tanto 10-17-23 como 23-17-10 como correcto.

Permutations: the hairy details

Let’s start with permutations, or all possible ways of doing something. Estamos usando o termo “permutação”, então vamos nos preocupar com cada detalhe, incluindo a ordem de cada item. Digamos que temos 8 pessoas:

1: Alice2: Bob3: Charlie4: David5: Eve6: Frank7: George8: Horatio

de quantas maneiras podemos premiar um 1º, 2º e 3º lugar entre oito concorrentes? (Ouro / Prata / Bronze)

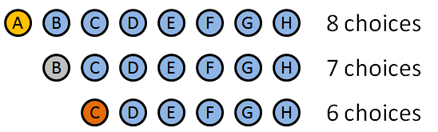
vamos usar permutações uma vez que a ordem que distribuímos estas medalhas importa. Aqui está como ele quebra:

• medalha de ouro: 8 Escolhas: A B C D E F G H (inteligente como eu fiz os nomes coincidir com as letras, eh?). Digamos que A ganha o ouro.medalha de prata: 7 escolhas: B C D E F G H. digamos que B ganha a prata.medalha de Bronze: 6 escolhas: C D E F G H. digamos … c ganha o bronze.

escolhemos certas pessoas para ganhar, mas os detalhes não importam: tivemos 8 escolhas no início, depois 7, depois 6. O número total de Opções foi $8 * 7 * 6 = 336$.vamos ver os detalhes. Tivemos de pedir 3 pessoas em cada 8. Para fazer isso, começamos com todas as opções (8), então as tiramos uma de cada vez (7, então 6) até que ficamos sem medalhas.sabemos que o factorial é:

infelizmente, isso faz demasiado! Só queremos $8 * 7 * 6$. Como podemos “parar” o fatorial às 5?

é aqui que as permutações ficam frias: repare como queremos livrar-nos $5 * 4 * 3 * 2 * 1$. Qual é outro nome para isto? 5 fatorial!então, se fizermos 8!/5! temos:

E por que nós usamos o número 5? Porque foi deixada depois de termos escolhido 3 medalhas de 8. Então, uma maneira melhor de escrever isso seria:

em que 8!/(8-3)! é apenas uma maneira chique de dizer ” Use os primeiros 3 números de 8!”. Se tivermos n itens totais e quisermos escolher k em uma determinada ordem, teremos:

e esta é a fórmula de permutação extravagante: você tem n itens e quer encontrar o número de formas como os itens k podem ser ordenados:

combinações, Ho!as combinações

são fáceis de utilizar. A ordem não importa. Podes misturá-lo e fica igual. Digamos que sou um forreta e não posso pagar medalhas separadas de Ouro, Prata e Bronze. Na verdade, só posso comprar latas vazias.quantas maneiras posso dar 3 latas a 8 pessoas?

bem, neste caso, a ordem que escolhemos as pessoas não importa. Se eu der uma lata à Alice, ao Bob e ao Charlie, é o mesmo que dar ao Charlie, à Alice e ao Bob. Seja como for, estão igualmente desapontados.isto levanta um ponto interessante-temos algumas redundâncias aqui. Alice Bob Charlie = Charlie Bob Alice. Por um momento, vamos descobrir de quantas maneiras podemos reorganizar três pessoas.

bem, temos 3 escolhas para a primeira pessoa, 2 para a segunda, e apenas 1 para a última. Então temos $3 * 2 * 1 maneiras de reorganizar 3 pessoas.espera um minuto… isto parece-se um pouco com uma permutação! Enganaste-me!de facto, fui eu. Se você tem N Pessoas e você quer saber quantos arranjos existem para todas elas, é apenas n factorial ou N!então, se temos 3 latas para dar, há 3! ou 6 variações para cada escolha que escolhermos. Se queremos descobrir quantas combinações temos, criamos todas as permutações e dividimos por todas as redundâncias. No nosso caso, obtemos 336 permutações (de cima), e dividimos pelas 6 redundâncias para cada permutação e obtemos 336/6 = 56.

A fórmula geral é

o que significa ” encontrar todas as formas de escolher as pessoas k de n, e dividir pelo k! variante”. Ao escrever isto, obtemos a nossa fórmula de combinação, ou o número de formas de combinar itens k de um conjunto de n:

às Vezes C(n,k) é escrito como:

qual é o coeficiente binomial.

alguns exemplos

Aqui estão alguns exemplos de combinações (a ordem não importa) de permutações (questões de ordem).combinação: escolher uma equipa de 3 pessoas de um grupo de 10. $C (10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.permutação: escolher um presidente, VP e Waterboy de um grupo de 10. $P (10,3) = 10!/7! = 10 * 9 * 8 = 720$.combinação

não memorize as fórmulas, entenda por que elas funcionam. Combinações soam mais simples que permutações, e são. Tens menos combinações do que permutações.

Outros Posts Desta Série

1. Fácil Permutações e Combinações
2. Navegar em uma Grade Usando Combinações E Permutações
3. Como Entender de Combinações Usando Multiplicação
4. Por que multiplicar combinações?