Números Complexos: Introdução (página 1 de 3)

as Seções: Introdução, Operações com complexos, A Fórmula Quadrática

até agora, lhe foi dito que você não pode tirar a raiz quadrada de um número negativo. Isso é porque você não tinha números que eram negativos depois que você os quadrou (para que você não pudesse “ir para trás” tomando a raiz quadrada). Todos os números foram positivos depois de o teres feito. Então você não poderia muito bem raiz quadrada a negativo e esperar chegar a qualquer coisa sensata.

agora, no entanto, você pode ter a raiz quadrada de um número negativo, mas envolve o uso de um novo número para fazê-lo. Este novo número foi inventado (descoberto?) por volta da época da Reforma. Naquela época, ninguém acreditava que qualquer uso do” mundo real ” seria encontrado para este novo número, além de facilitar os cálculos envolvidos na resolução de certas equações, então o novo número foi visto como sendo um número falso inventado por conveniência.

(mas então, quando você pensa sobre isso, não são todas invenções de números? Não é como se os números crescessem nas árvores! Vivem nas nossas cabeças. Inventámo-los todos! Porque não inventar um novo, desde que funcione bem com o que já temos?)

Então:

Agora, você pode pensar que você pode fazer isso:

Mas isso não faz qualquer sentido! Você já tem dois números que quadrado para 1, ou seja -1 e +1. E eu já fiz um quadrado para-1. Por isso, não é razoável que eu também seja igual a 1. Isto aponta um detalhe importante: Ao lidar com imaginários, você ganha algo (a capacidade de lidar com negativos dentro de raízes quadradas), mas você também perde algo (algumas da flexibilidade e regras convenientes que você costumava ter ao lidar com raízes quadradas). Em particular, você deve sempre fazer a parte i em primeiro lugar!

• Simplifique sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Todos os Direitos Reservados

(Aviso: O passo que vai até o terceiro “é igual a” o sinal ” “, e não ““. O i está fora do radical.)

• Simplifique sqrt (-25).

• Simplificar sqrt(-18).

• Simplificar –sqrt(-6).

Em seus cálculos, você vai lidar com eu, assim como você faria com x, exceto pelo fato de que x2 é só x2, mas i2 é igual a -1:

• Simplificar 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• Simplificar 16i – 5i.

16i – 5i = (16 – 5)i = 11i

• multiplique e simplifique (3i)(4i).

(3i)(4i) = (3·4)(i·i) = (12)(i2) = (12)(-1) = -12

• Multiplicar e simplificar (i)(2i)(–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

Nota este último problema. Dentro dele, você pode ver que , porque i2 = -1. Continuando, temos:

Este padrão de poderes, sinais, 1, e i é um ciclo:

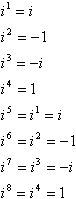
Em outras palavras, para calcular qualquer potência alta do que eu, você pode convertê-lo para um de menor potência tomando o mais próximo múltiplo de 4, que não é maior do que o expoente e subtraindo este múltiplo do expoente. Por exemplo, uma pergunta com rasteira comum em testes é algo ao longo das linhas de “simplificar i99”, a idéia é que você vai tentar multiplicar I noventa e nove vezes e você vai ficar sem tempo, e os professores vão ter uma boa risada às suas custas no salão da Faculdade. Veja como o atalho funciona:

i99 = i96+3 = i(4×24)+3 = i3 = –i

isto é, i99 = i3, porque você só pode cortar fora o i96. (Noventa e seis é um múltiplo de quatro, então i96 é apenas um, que você pode ignorar.) Em outras palavras, você pode dividir o expoente por 4 (usando divisão longa), descartar a resposta, e usar apenas o restante. Isso lhe dará a parte do expoente que você se preocupa. Aqui estão mais alguns exemplos:

• Simplifique i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

• Simplificar i120.

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

• Simplificar i64,002.

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>