Integrais Definidos
poderá gostar de ler a introdução à integração primeiro!
Integração
|
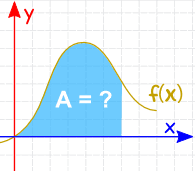
a Integração pode ser usado para localizar áreas, volumes, pontos centrais e muitas coisas úteis. Mas ele é frequentemente usado para encontrar a área sob o gráfico de uma função como esta: |
 |
|
|
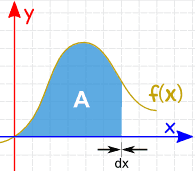
A área pode ser encontrada adicionando as fatias que se aproximar de zero de largura: E existem Regras de Integração que nos ajudam a obter a resposta. |
 |
Notação
O símbolo para “Integral” é um elegante “S” (de “Soma”, a idéia de soma fatias):
Após o Integral Símbolo colocamos a função que nós queremos encontrar a integral de (chamado de o Integrando).
e, em seguida, terminar com dx para significar que as fatias vão na direção x (e aproximar zero em largura).
Integral Definida
uma Integral Definida tem valores iniciais e finais: em outras palavras, há um intervalo .
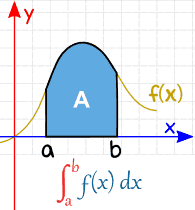
A E b (chamados limites, limites ou limites) são colocados no fundo e no topo do “S”, assim:
 |
 |
|
| Definite Integral (from a to b) |
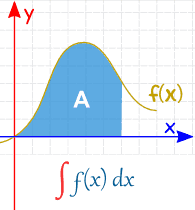
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
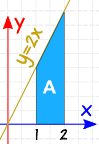
Exemplo: o Que é 2 ∫ 1 2x dx
Estamos sendo solicitados para a Integral Definida, de 1 para 2, 2x dx
Primeiro, precisamos encontrar a Integral Indefinida.
Usando as Regras de Integração descobrimos que ∫2x dx = x2 + C
Agora calcular que, no 1 e 2:
- x=1: ∫2x dx = 12 + C
- Em x=2: ∫2x dx = 22 + C
Subtrair:
E “C” fica cancelada … assim, com o Definitivo Integrais podemos ignorar C.
Resultado:

Verifique: com uma forma simples, vamos também tentar calcular a área de geometria:
Um = 2+42 × 1 = 3
Sim, ele tem uma área de 3.(Yay!)
Notação: Nós podemos mostrar a integral indefinida (sem o +C) dentro de colchetes, com os limites a e b, depois, como este:
Exemplo (continuação)
Uma boa maneira de mostrar a sua resposta:
=
Vamos tentar outro exemplo:
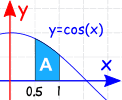
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
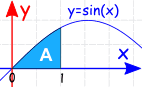
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
A Integral Indefinida é: ∫sin(x) dx = −cos(x) + C
uma vez que estamos indo de 0, podemos calcular a integral em x=1?
−cos(1) = – 0, 540…o quê? É negativo? Mas parece positivo no gráfico.bem … cometemos um erro!
porque precisamos subtrair a integral em x = 0. Não devemos assumir que é zero.então vamos fazer isso corretamente, subtraindo um do outro:
=
Mas podemos ter negativos regiões, quando a curva estiver abaixo do eixo:
Exemplo:
A Integral Definida, de 1 a 3, de cos(x) dx:
Observe que algumas delas são positivas, outras negativas.
a integral definitiva irá resolver o valor líquido. vamos fazer os cálculos.:
=
Salto há mais negativo do que positivo com o resultado líquido de -0,700….então temos uma coisa importante para recordar:
Tente integrar cos(x) com diferentes valores de início e término para ver por si mesmo como pontos positivos e negativos do trabalho.
área positiva
mas por vezes queremos que toda a área seja tratada como positiva (sem subtrair a parte abaixo do eixo).
nesse caso, devemos calcular as áreas separadamente, como no exemplo:

Exemplo: Qual é a área total entre y = cos (x) e o eixo x, de x = 1 A x = 3?
isto é como o exemplo que acabamos de dar, mas agora esperamos que toda a área seja positiva (imagine que tivemos que pintá-la).
Então, agora temos que fazer as peças separadamente:
- Um para a área acima do eixo-x
- Um para a área abaixo do eixo-x
A curva cruza o eixo x em x = π/2 assim, temos:
a Partir de 1 de π/2:
= sin(π/2) − sin(1)
a Partir de π/2 para 3:
= sin(3) − sin(π/2)
o último sai negativo, mas queremos que ela seja positiva, assim:
área Total = 0.159… + 0.859… = 1.018…
isto é muito diferente da resposta no exemplo anterior.
contínuo
Oh sim, a função que estamos integrando deve ser contínua entre a e b: sem Buracos, Saltos ou assintotas verticais (onde a função vai para cima/para baixo em direcção ao infinito).
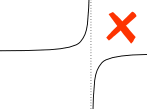
Exemplo:
Uma assíntota vertical entre a e b afeta a integral definida.
Propriedades
Área acima da área abaixo
A integral adiciona a área acima do eixo, mas subtrai a área abaixo, para um “valor líquido”:
Adicionar Funções
A integral de f+g é igual a integral de f plus a integral de g:
Inverter o intervalo
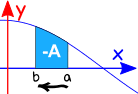
a Inversão da direcção do intervalo dá o negativo da direção original.
![]()


Leave a Reply