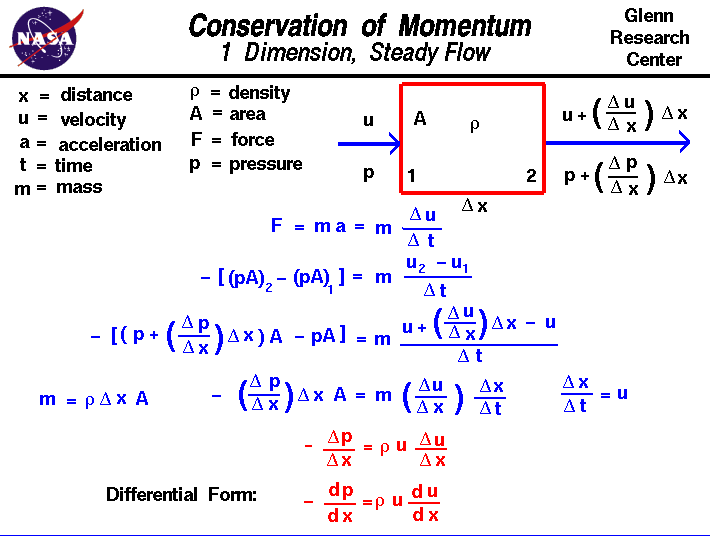
a conservação do momentum é um conceito fundamental da fisicsalong com a conservação da energia e a conservação da massa.O momento é definido como a massa de um objeto multiplicada pela velociidade do objeto.A conservação do momentum afirma que, dentro de algum domínio problemático, a quantidade de momentum permanece constante;o momentum não é criado nem destruído, mas apenas alterado através da ação de forças, como descrito pelas leis de movimento de Newton.Lidar com o momentum é mais difícil do que lidar com a massa e a energia, uma vez queomento é uma quantidadecector que tem uma magnitude e uma direcção. O momento é conservado em todas as direções triefísicas ao mesmo tempo. É ainda mais difícil quando se lida com agasbec porque as forças numa direcção podem afectar o momentum noutra direcção devido às colisões de muitas moléculas.Neste slide, vamos apresentar um problema de fluxo muito, muito simplificado, onde as propriedades só mudam em uma direção.O problema é ainda mais simplificado ao considerar um fluxo constante que não muda com o tempo e ao limitar as forças apenas aos associados com thepressure.Be conscientes de que os problemas reais de fluxo são muito mais complexos do que este exemplo simples.

vamos considerar o fluxo de um gás através de um domínio no qual o fluxo propertiesonly mudar em uma direção, que vamos chamar “x”. O gás entra na estação domainat 1 com alguma velocidade u e alguma pressão pand sai na estação 2 com um valor diferente de velocidade e pressão. Para simplificar, assumiremos que a densidade R permanece constante dentro do domínio e que a área A através da qual o gás flui também permanece constante. A localização das estações 1 e 2 é separada por uma distância chamada del X. (Delta é o pequeno triângulo no slideand é a letra grega “d”. Matemáticos muitas vezes usam este símbolo para denotear a mudança ou variação de uma quantidade. A fonte de impressão web não suporta as letras gregas, por isso vamos chamá-la de “del”.) Uma mudança com distância é referida como um gradiente para evitar confusão com uma mudança com o tempo que é chamado de taxa.O gradiente de velocidade é indicado por del u / del x; a variação na variação de velocidade na distância. Assim, na estação 2, a velocidade é dada pelo velocityat 1 Mais o gradiente vezes a distância.

:

Newton’ssecond lei do movimento de statesthat força F é igual à mudança na dinâmica withrespect tempo. Para um objecto com massa constante, isto reduz – se à massa vezes aceleração a.An a aceleração é uma mudança na velocidade com uma mudança no tempo (del u / del t). Então:

A força neste problemcomes do gradiente de pressão. Uma vez que a pressão é uma força por unidade de área,a força líquida no nosso domínio fluido é a pressão vezes a área no theexit menos a pressão vezes a área na entrada.

O sinal de subtração sentado início desta expressão é usada porque os gases se mover de um regionof de alta pressão para uma região de baixa pressão; se a pressão aumenta withx, a velocidade irá diminuir. Substituindo as nossas expressões para velocityand pressão:

Simplificar:

Notar que o del (x / del t) é thevelocity e que a massa é a densidade de r vezes o volume (área de vezes del x):

Simplificar:

O del p / del x e del u / del xrepresent a pressão e a velocidade de gradientes.Se vamos reduzir o nosso domínio para baixo diferencial de tamanhos, estes gradientes de se tornar diferenciais:

Este é um dimensionais, constante do formulário ofEuler da Equação.É interessante notar que a pressão dropof um fluido (o termo à esquerda) é proporcional ao valor de thevelocity e o gradiente de velocidade.Uma solução desta equação de momento nos dá a forma da pressura dinâmica que aparece na equação de inBernoulli.actividades:
Guided Tours

• Basic Fluid Dynamics Equations:

Navigation ..

Beginner’s Guide Home Page