Evaluating Cohen’s Kappa

O valor para kappa pode ser inferior a 0 (negativo). Uma pontuação de 0 significa que existe um acordo aleatório entre os raters, enquanto uma pontuação de 1 significa que existe um acordo completo entre os raters. Portanto, uma pontuação que é inferior a 0 significa que há menos Acordo do que chance aleatória. Abaixo, eu vou mostrar a fórmula para resolver isso, mas é importante que você se familiarize com a figura 4 para ter uma compreensão forte.

A razão de eu destaquei duas grades, ficará claro em um momento, mas por agora, deixe-me quebrar de cada grade.

a = > o número total de instâncias que ambos os raters disseram estarem corretas. Os Raters estão de acordo.

b = > o número total de instâncias que Rater 2 disse estava incorreto, mas Rater 1 disse estavam corretas. Isto é um desacordo.

C = > o número total de instâncias que Rater 1 disse estava incorreto, mas Rater 2 disse estavam corretas. Isto também é um desacordo.

D = > o número total de instâncias que ambos os Raters disseram estarem incorretas. Os Raters estão de acordo.

A fim de determinar o valor kappa, precisamos primeiro de saber a probabilidade de acordo (isto explica porque realcei a diagonal do acordo). Esta fórmula obtém-se adicionando o número de testes em que as taxas concordam e dividindo-o pelo número total de testes. Usando o exemplo da figura 4, isso significaria(A + D)/(A + B+ C+ D).

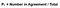
Perfeito! O próximo passo é determinar a probabilidade de um acordo Aleatório. Usando a figura 4 como um guia, o valor esperado é o número total de vezes em que o Examinador 1 disse correta, dividido pelo número total de instâncias, multiplicado pelo número total de vezes em que o Examinador 2 disse correta, dividido pelo número total de instâncias, adicionado ao número total de vezes em que o Examinador 1 disse incorreto multiplicado pelo número total de vezes em que o Examinador 2 disse incorreta. Essa é uma grande quantidade de informação para levar lá, então na Figura 6 Eu formulei esta equação usando a grade acima.

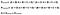
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

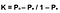
Great! Agora você é capaz de distinguir entre confiabilidade e validade, explicar a kappa de Cohen e avaliá-la. Esta estatística é muito útil, embora já que eu entendi como ela funciona, eu agora acredito que ela pode ser sub-utilizada ao otimizar algoritmos para uma métrica específica. Além disso, a kappa de Cohen também faz um bom trabalho na medição de ambos os problemas de classe multi e desequilibrada.

P. S. Se há algo que você quer que eu cubra a respeito da ciência dos dados, você pode me dirigir uma mensagem no Twitter @KurtisPykes ou deixar uma resposta a este post.