beanz Revista
Mapa por Merian-Erben (1652) na Wikipédia
Este mês quebra-cabeças de matemática remonta a 1735, quando foi resolvido por Leonhard Euler, um Suíço, matemático e físico.o quebra-cabeças é chamado de Sete Pontes de Königsberg. É baseado numa cidade real, depois na Prússia, agora Kaliningrado na Rússia. A cidade é dividida por um rio com duas ilhas no meio e, mais abaixo, o rio divide a cidade novamente.
O problema é enganosamente simples: Há (ou eram, no tempo de Euler) sete pontes para conectar as duas ilhas e as partes a jusante da cidade. Euler se perguntou se uma pessoa poderia caminhar através de cada uma das Sete Pontes uma vez e apenas uma vez para tocar todas as partes da cidade. Começar e terminar no mesmo local não era um requisito.
Aqui está um mapa que você pode usar para tentar resolver o problema por si mesmo:
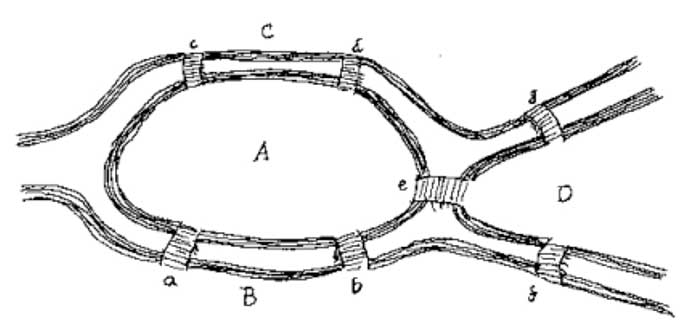
o Que você acha que é mais importante para resolver este problema: o número de pontes ou a localização de cada ponte?resposta: o número de pontes.
Euler provou que o número de pontes deve ser um número par, por exemplo, seis pontes em vez de sete, se você quiser andar sobre cada ponte uma vez e viajar para cada parte de Königsberg. A solução vê cada ponte como um ponto final, um vértice em termos matemáticos, e as conexões entre cada ponte (vértice). Euler percebeu que apenas um número par de pontes rendeu o resultado correto de ser capaz de tocar todas as partes da cidade sem cruzar uma ponte duas vezes.Euler usou matemática para provar que era impossível cruzar todas as sete pontes apenas uma vez e visitar cada parte de Königsberg. Ao fazê-lo, ele pôs em movimento uma série de descobertas e insights sobre como o espaço e os espaços de intersecção podem ser definidos, bem como suas propriedades. A detailed description of Euler’s solution in the Wikipedia link below this article.se você já viu uma faixa de mobius, por exemplo, você viu um exemplo de topologia, um campo de estudo matemático evoluiu da solução de Euler para este problema. A topologia está preocupada com o espaço e como as coisas se conectam umas às outras, bem como com a continuidade e os limites do espaço. A topologia também estuda como as propriedades de uma mudança de espaço e não mudam quando o espaço é expandido ou contraído.
em computação, topologia é útil na compreensão dos dados de redes (caminhos) podem fluir dentro de qualquer sistema, bem como como como conjuntos de dados podem se relacionar uns com os outros. As Sete Pontes de Königsberg também é semelhante a outro problema comum de computação chamado às vezes o problema do vendedor ambulante, onde você tenta encontrar a rota mais eficiente dada um conjunto de restrições como as sete pontes no problema de Euler.
não-matemáticos (provavelmente você, definitivamente eu) experimentam o problema do Caixeiro Viajante sempre que entramos em um trem ou ônibus. O problema do Caixeiro Viajante é descobrir a maneira mais eficiente de viajar entre pares de cidades de distâncias especificadas. Gerir recursos escassos (comboios, autocarros) que viajam ao longo de rotas finitas é um problema perfeito para a computação resolver porque os computadores são mais rápidos e mais eficientes. Mas primeiro precisamos que Euler e outros afirmem o problema e definam soluções com matemática. Então programamos nossos computadores para fazer as contas.
topologia também lida com a teoria dos conjuntos, como grupos de coisas podem ser classificados em conjuntos para identificar elementos comuns com outros grupos, bem como elementos únicos. Um diagrama de Venn é um grande exemplo de um conjunto. E programação às vezes tem que classificar os dados de maneiras diferentes. Qual método de ordenação funciona melhor para uma situação pode ser determinado pela teoria dos conjuntos.e o que aconteceu às sete pontes do tempo de Euler? Duas pontes foram demolidas e substituídas por uma única estrada. Das três pontes restantes, uma foi reconstruída em 1935, enquanto as outras duas permanecem intactas como Euler as conhecia. E, claro, Königsberg, a Prússia mudou seu nome para Kaliningrado, Rússia.
Leave a Reply