a matemática é mais uma maratona do que um sprint — é um moinho longo, lento e estável, com raros momentos de avanço. Ainda assim, de vez em quando, temos aqueles momentos “Eureka” premiados, aquelas linhas curtas de letras e números que mudam a ciência para sempre. Aqui estão algumas das equações mais famosas, dos gregos antigos à física moderna.

teorema de Pitágora (530 A. C.)

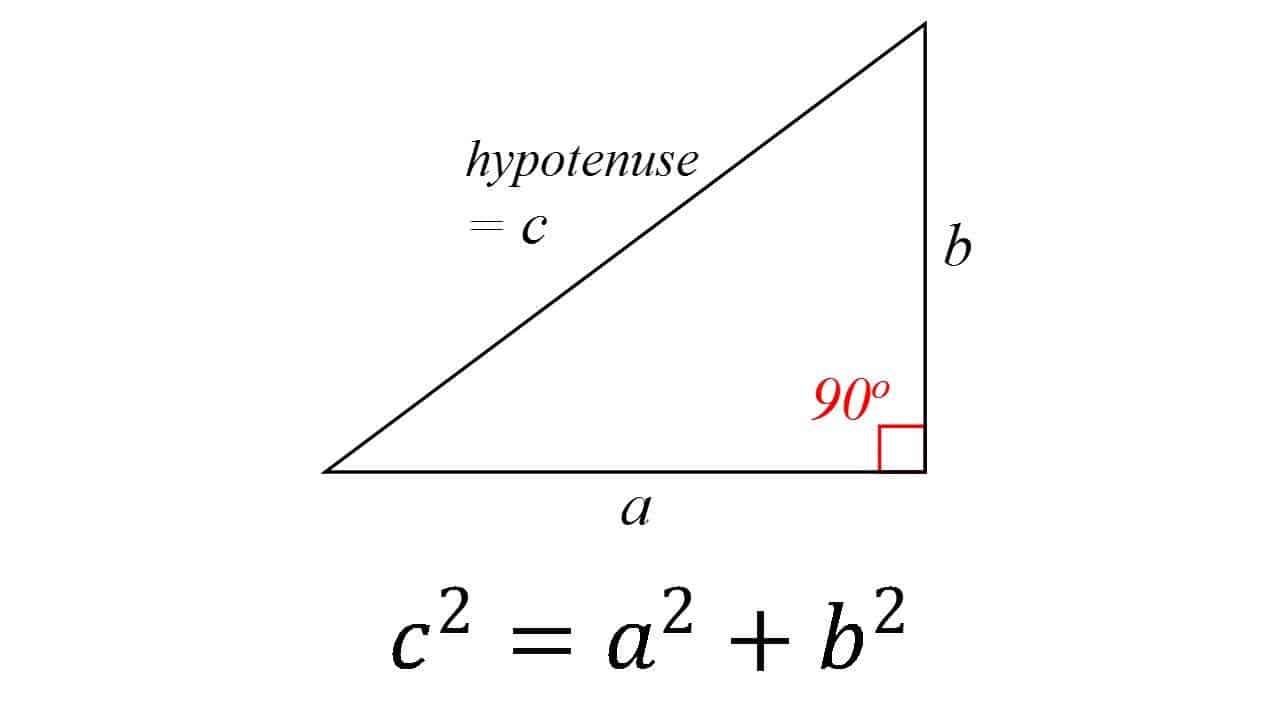
Este é um dos pilares fundamentais de toda a geometria: em um triângulo retângulo, o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos outros dois. A teoria é geralmente atribuída ao matemático grego Pitágoras, embora haja alguma evidência de que matemáticos babilônicos compreendessem a fórmula. Também é muito possível que o teorema fosse conhecido por muitas pessoas, mas ele foi o primeiro a prová-lo.

O teorema tem sido dado numerosas provas — possivelmente a mais para qualquer teorema matemático. Eles são muito diversos, incluindo provas geométricas e provas algébricas, com alguns datando de milhares de anos.

números Complexos

O matemático italiano Gerolamo Cardano é a primeira a introduzir os números complexos, chamando-os de “fictício” no momento. No entanto, o desenvolvimento matemático de “i” como o número imaginário representando a raiz quadrada de -1 é atribuído a Leonhard Euler, um dos matemáticos e cientistas mais importantes da história humana.

números complexos são basicamente números que não existem realmente, mas que são muito úteis para uma série de cálculos. Eles consistem em números com uma parte real (os números que todos conhecemos) e uma parte imaginária (o eu representado aqui) e têm aplicações práticas em muitos campos, incluindo Física, Química, Biologia, Economia, Engenharia Elétrica e Estatística.

Os logaritmos

Logaritmos são, basicamente, a função inversa de exponenciação. Você precisa de um número (N), uma base (um), e o logaritmo de N na base de um x, onde N é igual à potência de x. Pode parecer apenas uma forma diferente de escrever a mesma coisa (e, em certo sentido, ele é), mas logaritmos têm uma infinidade de aplicações práticas, sendo utilizados na psicologia, economia, e as medições de muitos fenômenos físicos (como o pH ou o terremoto de magnitude).

Logaritmos foram publicamente defendido por John Napier, em 1614, em um livro intitulado ” Mirifici Logarithmorum Canonis * Competitiv (Descrição da Maravilhosa Regra dos Logaritmos) — um título adequado. Um caso especial de logaritmo é o logaritmo natural-e, onde e é um número irracional e transcendental aproximadamente igual a 2,71828182845. Na verdade, o próprio e tem uma história fascinante e um número impressionante de aplicações, mas isso é uma história para outra altura.

cálculo

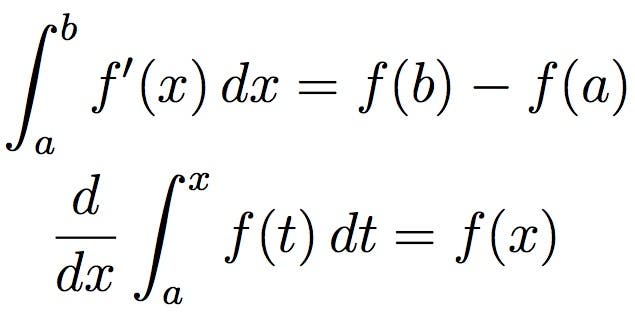
poucos campos da matemática têm sido tão impactantes como o cálculo. Desenvolvido no século XVII por Isaac Newton e Gottfried Wilhelm Leibniz, o cálculo é amplamente utilizado na ciência, engenharia e economia. O cálculo geralmente se concentra em lidar com pequenas quantidades, particularmente quantidades infinitamente pequenas. Através do cálculo, estes podem ser tratados como números reais, mesmo que sejam tecnicamente infinitamente pequenos.

para uma visualização mais simples, a integração, representada acima, pode ser considerada como medindo a área sob uma curva, definida por uma função.por falar em Newton, ele também é “responsável” por uma das equações mais famosas e espetaculares do mundo: a lei da gravidade.

a lei basicamente descreve como quaisquer dois corpos de massas m1 e m2 são atraídos um pelo outro. A força (F1, F2) é inversamente proporcional ao quadrado da distância entre eles (r). O único fator remanescente, G, é uma constante gravitacional. A natureza desta constante permanece esquiva.

a Relatividade Geral

Por quase 200 anos, a lei de Newton definiu o nosso nível de compreensão da mecânica. O trabalho de Einstein no século XX levou as coisas para o próximo nível — estas duas conquistas Torre nos pedestais mais altos do mundo da física.

a relatividade Geral é, essencialmente, uma teoria geométrica da gravitação, generalizando a teoria de Newton fornecendo uma descrição unificada da gravidade como uma propriedade geométrica do espaço e do tempo, ou espaço-tempo. Em particular, Einstein mostrou não só que não há tal coisa como “espaço-tempo” da fusão das três dimensões com a 4ª dimensão do tempo, mas ele também mostrou que esse espaço-tempo pode ser curvada pela gravidade, com a curvatura estar directamente relacionados com a energia e o momentum de qualquer matéria e radiação estão presentes.

Segunda lei da termodinâmica

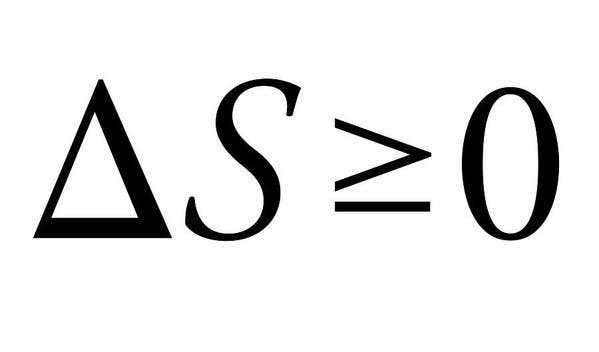
A Segunda Lei da Termodinâmica é por isso que não podemos ter coisas boas no Universo. Piadas à parte, as quatro leis da termodinâmica definem quantidades físicas fundamentais (temperatura, energia e entropia) que caracterizam os sistemas termodinâmicos. A segunda, em particular, destaca-se aqui devido à sua simplicidade, mas com implicações absolutamente massivas.

a lei essencialmente afirma que a soma das entropias dos sistemas termodinâmicos interativos deve sempre aumentar, ou no máximo permanecer constante. Quando a energia muda de uma forma para outra ou a matéria se move ao redor, a entropia (ou desordem) em um sistema fechado aumenta. Todas as diferenças de temperatura, pressão e densidade tendem a televisão fora depois de um tempo

as Equações de Maxwell

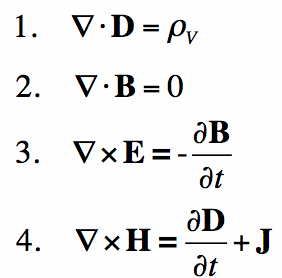
simplificando, as equações de Maxwell são para o eletromagnetismo que a lei de Newton está para a mecânica. Eles fornecem uma base matemática para eletromagnetismo clássico, óptica clássica e circuitos elétricos. Eles são amplamente utilizados no próprio dispositivo que você está lendo isto-basicamente, todos os dispositivos eletrônicos.as leis de Maxwell descrevem como campos elétricos e magnéticos são gerados por cargas, correntes e mudanças dos Campos. Um avanço significativo foi a demonstração de que campos elétricos e magnéticos se propagam à velocidade da luz.

Euler de Identidade

por último, este é possivelmente o mais elegante equação, uma coisa de suprema beleza, porque envolve todos os “basic” números:

• 0, que é neutro para a adição e subtração;
• 1, o que é neutro para a multiplicação e divisão;
• e, o que é o número de Euler (ver acima), a base dos logaritmos naturais;
• i é a unidade imaginária (ver acima); e
• π É pi, A razão entre a circunferência de um círculo e o seu diâmetro.

encontrar uma relação que unifique todos estes números não é nada menos do que tirar o fôlego, e parece bastante improvável. A demonstração não é exatamente simples, mas você pode vê-la aqui.

É justo que a Universidade de Stanford matemática professor Keith Devlin descrito na equação, dizendo que “como um soneto Shakespeariano que capta a essência do amor, ou uma pintura que traz a beleza da forma humana que é muito mais do que apenas a pele profunda, Euler equação desce às profundezas da existência”

não É sempre que a matemática e a física se resumem a simples e elegante equações, mas quando o fazem, é um espetáculo para ser visto.