o tutorial explica os fundamentos da análise de regressão e mostra algumas maneiras diferentes de fazer regressão linear no Excel.

Imagine isto: você é fornecido com um monte de dados diferentes e é solicitado a prever os números de vendas do próximo ano para a sua empresa. Descobriu dezenas, talvez até centenas, de factores que podem afectar os números. Mas como é que sabes quais são realmente importantes? Executar a análise de regressão no Excel. Dar-lhe-á uma resposta a isto e a muitas mais perguntas.: Que factores são importantes e que podem ser ignorados? Qual é a relação entre estes factores? E quão certo você pode estar sobre as previsões?

• análise de Regressão no Excel
• de regressão Linear do Excel com Ferramentas de Análise
• Desenhar-se uma regressão linear do gráfico
• análise de Regressão no Excel com fórmulas

a análise de Regressão no Excel – noções básicas

Em modelagem estatística, a análise de regressão é utilizada para estimar as relações entre duas ou mais variáveis:

variável dependente (aka variável critério) é o principal fator que você está tentando entender e prever.

variáveis independentes (também conhecidas como variáveis explicativas, ou predictores) são os fatores que podem influenciar a variável dependente.

Análise de regressão ajuda você a entender como a variável dependente muda quando uma das variáveis independentes varia e permite determinar matematicamente qual dessas variáveis realmente tem um impacto.tecnicamente, um modelo de análise de regressão é baseado na soma dos quadrados, que é uma forma matemática de encontrar a dispersão dos pontos de dados. O objetivo de um modelo é obter a menor soma possível de quadrados e desenhar uma linha que se aproxima dos dados.

em estatísticas, eles diferenciam entre uma regressão linear simples e múltipla. A regressão linear simples modela a relação entre uma variável dependente e uma variável independente usando uma função linear. Se você usar duas ou mais variáveis explicativas para prever a variável dependente, você lida com regressão linear múltipla. Se a variável dependente for modelada como uma função não-linear porque as relações de dados não seguem uma linha reta, use regressão não-linear. O foco deste tutorial será em uma regressão linear simples.como exemplo, vamos pegar números de vendas de guarda-chuvas para os últimos 24 meses e descobrir a precipitação média mensal para o mesmo período. O grī informações em um gráfico, e a linha de regressão irá demonstrar a relação entre a variável independente (pluviosidade) e a variável dependente (guarda-chuva de vendas):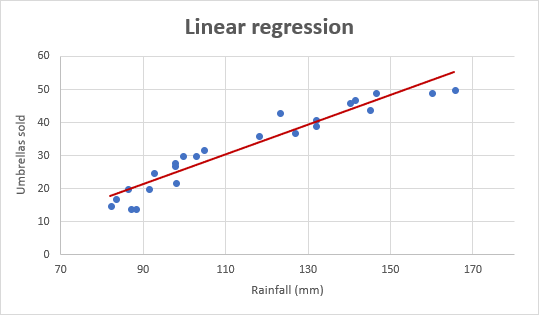

equação de regressão Linear

Matematicamente, uma regressão linear, é definido pela equação:

, Onde:

• x é uma variável independente.
• y é uma variável dependente.
• A é a interceptação em Y, que é o valor médio esperado de y quando todas as variáveis em x são iguais a 0. Num gráfico de regressão, é o ponto onde a linha atravessa o eixo Y.
• b é o declive de uma linha de regressão, que é a taxa de variação para y como X alterações.
• ε é o termo de erro aleatório, que é a diferença entre o valor real de uma variável dependente e o seu valor previsto.

a equação de regressão linear sempre tem um termo de erro porque, na vida real, os predictores nunca são perfeitamente precisos. No entanto, alguns programas, incluindo o Excel, fazem o cálculo do termo erro nos bastidores. Assim, no Excel, você pode fazer a regressão linear usando o método dos mínimos quadrados e buscar os coeficientes a e b tais que:

Para o nosso exemplo, a equação de regressão linear assume a seguinte forma:

Umbrellas sold = b * rainfall + a

existem um punhado de maneiras diferentes para encontrar a e b. Os três principais métodos para realizar a análise de regressão linear do Excel são:ferramenta de regressão

• incluída com a Ferramenta de análise Gráfico de dispersão com uma fórmula de regressão Linear

abaixo encontrará as instruções detalhadas sobre a utilização de cada método.

como fazer regressão linear no Excel com ferramenta de análise ToolPak

este exemplo mostra como executar regressão no Excel usando uma ferramenta especial incluída com a ferramenta de análise add-in ToolPak.

active a Ferramenta de análise add-in

Analysis ToolPak está disponível em todas as versões do Excel 2019 a 2003, mas não está activa por omissão. Tens de o ligar manualmente. Aqui está como:

1. no seu Excel, clique em Arquivo > opções.
2. na janela de Opções do Excel, seleccione Adicionar-ins na barra lateral esquerda, certifique-se que o Excel Add-ins está seleccionado na caixa de gestão e carregue em ir.
   
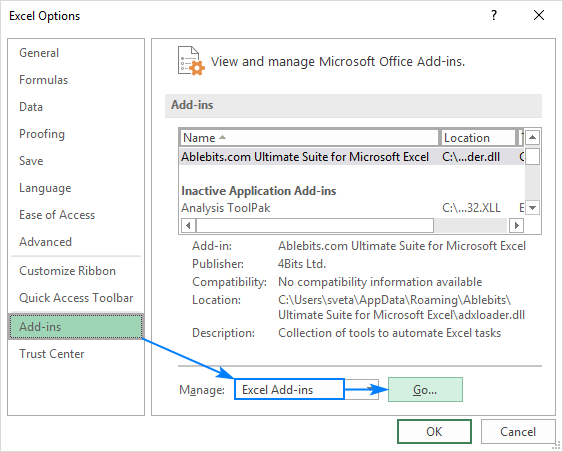
3. Na caixa de diálogo suplementos, marque Ferramentas de Análise e clique em OK:
   

Isto irá adicionar as ferramentas de Análise de Dados para os Dados do guia de faixa de opções do Excel.

executar a análise de regressão

neste exemplo, vamos fazer uma regressão linear simples no Excel. O que temos é uma lista de precipitação média mensal nos últimos 24 meses na coluna B, que é a nossa variável independente (predictor), e o número de guarda-chuvas vendidos na coluna C, que é a variável dependente. É claro, existem muitos outros fatores que podem afetar as vendas, mas agora vamos focar apenas estas duas variáveis: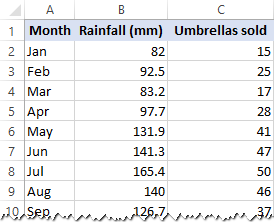

Com Ferramentas de Análise adicionado ativado, execute estas etapas para executar a análise de regressão no Excel:

1. Na guia Dados, no grupo de Análise, clique em Análise de Dados de botão.
   
2. selecione regressão e clique em OK.
   
3. Na janela de regressão, configure as seguintes opções:
   • Seleccione o intervalo y de entrada, que é a sua variável dependente. No nosso caso, São vendas de guarda-chuva (C1: C25).
   • Seleccione o intervalo X de entrada, ou seja, a sua variável independente. Neste exemplo, é a precipitação média mensal (B1: B25).

   Se estiver a construir um modelo de regressão múltipla, seleccione duas ou mais colunas adjacentes com variáveis independentes diferentes.

   • assinale a opção Etiquetas se existirem cabeçalhos no topo dos seus intervalos X e Y.
   • escolha a sua opção de saída preferida, uma nova folha de trabalho no nosso caso.
   • opcionalmente, selecione a caixa de seleção de resíduos para obter a diferença entre os valores previstos e reais.
     
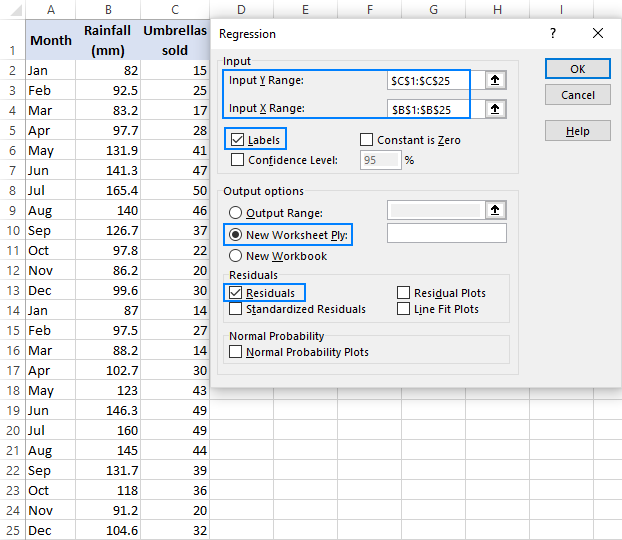
4. clique em OK e observe a saída da análise de regressão criada pelo Excel.

interpretar a saída da análise de regressão

como você acabou de ver, a regressão em execução no Excel é fácil porque todos os cálculos são pré-formados automaticamente. A interpretação dos resultados é um pouco mais complicada porque você precisa saber o que está por trás de cada número. Abaixo você encontrará uma repartição de 4 partes principais da saída da análise de regressão.

resultado da análise de regressão: resultado Sumário

esta parte diz-lhe quão bem a equação de regressão linear calculada se encaixa nos seus dados de origem.

Aqui está o que cada pedaço de informação significa:

múltiplo R. é o coeficiente de correlação que mede a força de uma relação linear entre duas variáveis. O coeficiente de correlação pode ser qualquer valor entre -1 e 1, e seu valor absoluto indica a força da relação. Quanto maior o valor absoluto, mais forte a relação:

• 1 significa uma forte relação positiva
• -1 significa uma forte relação negativa
• 0 significa que nenhum relacionamento em todos os

de R Quadrado. É o coeficiente de determinação, que é usado como um indicador da bondade do ajuste. Mostra quantos pontos caem na linha de regressão. O valor R2 é calculado a partir da soma total dos quadrados, mais precisamente, é a soma dos desvios ao quadrado dos dados originais da média.

no nosso exemplo, R2 é 0.91 (arredondado a 2 dígitos), o que é bom para as fadas. Isso significa que 91% dos nossos valores se encaixam no modelo de análise de regressão. Em outras palavras, 91% das variáveis dependentes (y-values) são explicadas pelas variáveis independentes (x-values). Geralmente, R ao quadrado de 95% ou mais é considerado um bom ajuste.quadrado R ajustado. É o quadrado R ajustado para o número de variável independente no modelo. Você vai querer usar este valor em vez de R quadrado para análise de regressão múltipla.erro padrão. É outra medida de bondade – de-ajuste que mostra a precisão de sua análise de regressão-quanto menor o número, mais certeza você pode estar sobre a sua equação de regressão. Enquanto R2 representa a porcentagem das variáveis dependentes variância que é explicada pelo modelo, o erro padrão é uma medida absoluta que mostra a distância média que os pontos de dados caem da linha de regressão.observações. É simplesmente o número de observações no seu modelo.

uma análise de Regressão de saída: ANOVA

A segunda parte do resultado é de Análise de Variância (ANOVA):

Basicamente, divide-se a soma dos quadrados em componentes individuais que fornecem informações sobre os níveis de variabilidade dentro de seu modelo de regressão:

• df é o número de graus de liberdade associado com as fontes de variação.
• SS é a soma dos quadrados. Quanto menor o SS Residual comparado com o total SS, melhor o seu modelo se encaixa nos dados.
• MS é o quadrado médio.
• F é a estatística de F, ou o teste de F para a hipótese nula. É utilizado para testar o significado geral do modelo.
• significância F é o valor P de F.

a parte ANOVA é raramente usada para uma análise de regressão linear simples no Excel, mas você deve definitivamente ter uma visão de perto do último componente. A significância do valor F dá uma idéia de quão confiáveis (estatisticamente significantes) seus resultados são. Se o Significado F for inferior a 0,05 (5%), o seu modelo está OK. Se for maior que 0,05, é melhor escolher outra variável independente.

uma análise de Regressão de saída: coeficientes

Esta seção fornece informações específicas sobre os componentes de sua análise:

O mais útil de componentes nesta seção é Coeficientes. Ele permite que você para construir uma equação de regressão linear do Excel:

Para o nosso conjunto de dados, onde y é o número de guarda-chuvas vendidos e x é uma precipitação média mensal, o nosso regressão linear fórmula é o seguinte:

Y = Rainfall Coefficient * x + Intercept

Equipados com valores a e b arredondado a três casas decimais, ele se transforma em:

Y=0.45*x-19.074

Por exemplo, com a precipitação média mensal igual a 82 mm, o guarda-chuva de vendas seria de cerca de 17,8:

0.45*82-19.074=17.8

Em uma maneira semelhante, você pode descobrir quantos guarda-chuvas vão ser vendidos com qualquer outro mensais de precipitação (variável x) você especificar.resultados da análise de regressão: resíduos

se comparar o número estimado e real de guarda-chuvas vendidas correspondente à precipitação mensal de 82 mm, verá que estes números são ligeiramente diferentes:

• estimado: 17.8 (calculado acima)
• Actual: 15 (Linha 2 dos dados de base)

porquê a diferença? Porque variáveis independentes nunca são preditores perfeitos das variáveis dependentes. E os resíduos podem ajudá-lo a entender quão longe estão os valores reais dos valores previstos:

como fazer um gráfico de regressão linear no Excel

Se você precisar visualizar rapidamente a relação entre as duas variáveis, desenhe um gráfico de regressão linear. Isso é muito fácil! Eis como:

1. seleccione as duas colunas com os seus dados, incluindo os cabeçalhos.
2. Na Inserção, na guia bate-Papos de grupo, clique em gráfico de Dispersão ícone, e selecione a Dispersão de miniaturas (o primeiro):
   

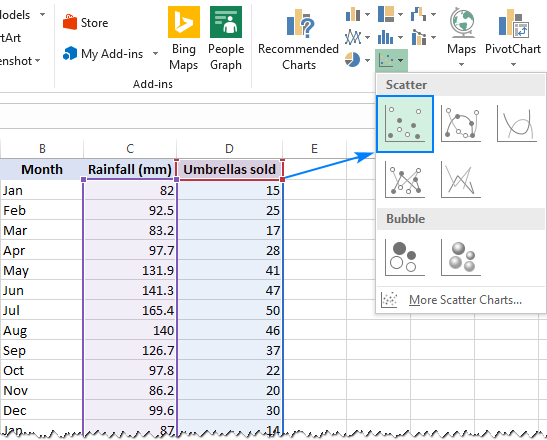
   Isto irá inserir um gráfico de dispersão na folha de cálculo, que será semelhante a este:
   

3. Agora, precisamos desenhar a linha de regressão de mínimos quadrados. Para o fazer, carregue com o botão direito em qualquer ponto e escolha Adicionar a linha de Trendline… do menu de contexto.
   
4. No painel direito, selecione a linha de tendência Linear da forma e, opcionalmente, marque a opção Exibir Equação no Gráfico para obter a sua fórmula de regressão:
   

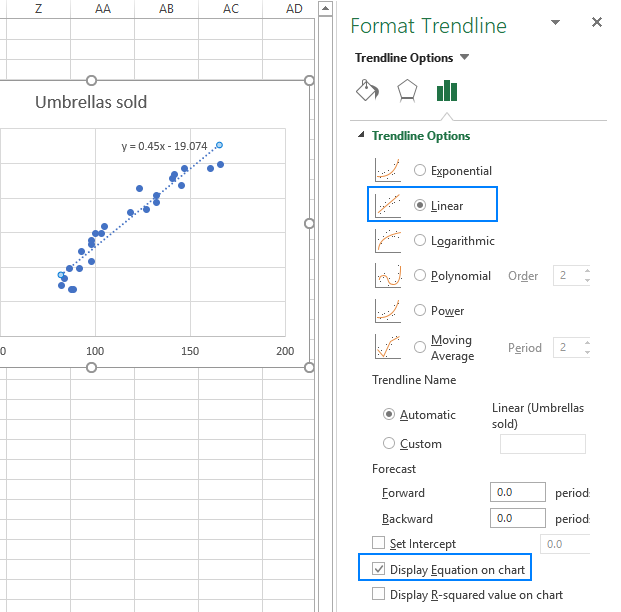
   Como você pode observar, a equação de regressão do Excel criou para nós é o mesmo que o de regressão linear fórmula construímos com base em Coeficientes de saída.

5. mude para a página Fill & linha e personalize a linha de acordo com o seu gosto. Por exemplo, você pode escolher outra cor de linha e usar uma linha sólida em vez de uma linha tracejada (selecione a linha Sólida no Traço tipo caixa):
   

neste ponto, o gráfico já parece digno de uma regressão gráfico:

Ainda, você pode querer fazer mais algumas melhorias:

• Arraste a equação onde quer que você vê o ajuste.
• adicionar títulos de eixos (botão de elementos de gráfico > títulos do eixo).se os seus pontos de dados começarem no meio do eixo horizontal e/ou vertical, como neste exemplo, poderá querer livrar-se do espaço branco excessivo. A seguinte dica explica como fazer isso: Escale os eixos do gráfico para reduzir o espaço em branco.

  And this is how our improved regression graph looks like:
  

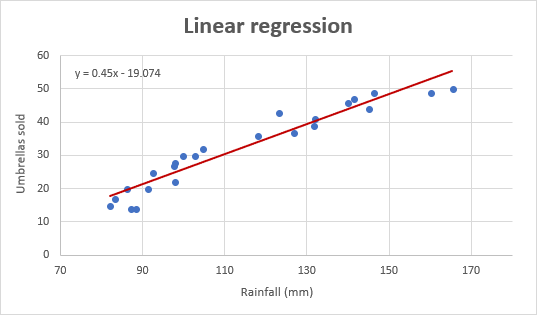  Important note! No grafo de regressão, a variável independente deve estar sempre no eixo X e a variável dependente no eixo Y. Se o seu gráfico for representado na ordem inversa, troque as colunas na sua folha de trabalho e, em seguida, desenhe o gráfico de novo. Se não lhe for permitido reorganizar os dados de origem, então poderá mudar os eixos X e Y directamente num gráfico.

Como fazer regressão no Excel usando fórmulas

o Microsoft Excel tem algumas funções estatísticas que podem ajudá-lo a fazer a análise de regressão linear, como LINEST, declive, INTERCEPET e CORREL.

A função LINEST utiliza o método de regressão dos mínimos quadrados para calcular uma linha recta que melhor explica a relação entre as suas variáveis e devolve uma matriz que descreve essa linha. Você pode encontrar a explicação detalhada da sintaxe da função neste tutorial. Por agora, vamos apenas fazer uma fórmula para o nosso conjunto de dados de amostra:

=LINEST(C2:C25, B2:B25)

porque a função LINEST devolve um conjunto de valores, você deve introduzi-lo como uma fórmula de matriz. Seleccionar duas células adjacentes na mesma linha, E2:F2 no nosso caso, escreva a fórmula e carregue em Ctrl + Shift + Enter para a completar.

A fórmula devolve a b coeficiente (E1) e a uma constante (F1) para os já familiarizados equação de regressão linear:

y = bx + a

Se você evitar o uso de fórmulas de matriz em suas planilhas, você pode calcular a e b, individualmente, com regular fórmulas:

a intercepção de Y (a):

=INTERCEPT(C2:C25, B2:B25)

a inclinação (b):

=SLOPE(C2:C25, B2:B25)

Além disso, você pode encontrar o coeficiente de correlação (R Múltiplos na análise de regressão resumo de saída) que indica o quão fortemente as duas variáveis estão relacionadas entre si:

=CORREL(B2:B25,C2:C25)

A captura de tela a seguir mostra todos estes Excel fórmulas de regressão em ação:

É assim que se faz regressão linear no Excel. Dito isto, tenha em mente que o Microsoft Excel não é um programa estatístico. Se você precisar realizar a análise de regressão a nível profissional, você pode querer usar software alvo, tais como XLSTAT, RegressIt, etc.

downloads disponíveis:

para ter uma olhada mais de perto nas nossas fórmulas de regressão linear e outras técnicas discutidas neste tutorial, você é bem-vindo para baixar a nossa análise de regressão de amostras no Excel workbook.

• Como usar o Solver no Excel com exemplos
• Como calcular juros compostos no Excel
• Como calcular CAGR (taxa de crescimento anual composta) no Excel