amplitudes Interquartis & Outliers
Quartis & Boxes5-Número SummaryIQRs & Outliers
Purplemath
O “intervalo interquartílico”, abreviado “IQR”, é apenas a largura da caixa em caixa-e-bigodes. Isto é, IQR = Q3 – Q1 . O IQR pode ser usado como uma medida de como os valores são distribuídos.
as Estatísticas assumem que os seus valores estão agrupados em torno de algum valor central. O IQR diz como se espalham os valores “médios”; ele também pode ser usado para dizer quando alguns dos outros valores estão” muito longe ” do valor central. Estes pontos ” muito distantes “são chamados de” anómalos”, porque eles” estão fora ” da faixa em que nós os esperamos.
o QI é o comprimento da caixa na sua parcela de caixa e bigodes. An outlier is any value that lies more than one and a half times the length of the box from each end of the box.
o conteúdo continua abaixo de
MathHelp.com
isto é, se um ponto de dados é abaixo de Q1 – 1.5×IQR ou acima de Q3 + 1.5×IQR, ele é visto como sendo muito longe da central de valores razoáveis. Talvez tenhas batido na balança quando estavas a fazer aquela medição, ou talvez o teu parceiro de laboratório seja um idiota e nunca o devias ter deixado tocar em nenhum dos equipamentos. Quem sabe? Mas seja qual for a sua causa, os pontos anómalos são aqueles que não parecem “encaixar”.
Why one and a half times the width of the box for the outliers? Por que esse valor em particular demarca a diferença entre valores “aceitáveis” e “inaceitáveis”? Porque, quando John Tukey estava inventando o enredo de box-and-whisker em 1977 para exibir esses valores, ele escolheu 1.5×IQR como a linha de demarkation para valores anómalos. Isto tem funcionado bem, por isso continuamos a usar esse valor desde então. Se você for mais longe nas estatísticas, você vai descobrir que esta medida de razoabilidade, para dados em forma de curva de sino, significa que geralmente apenas talvez tanto quanto cerca de um por cento dos dados serão sempre anómalos.
pode usar o elemento Mathway abaixo para praticar a procura do intervalo interquartil, também chamado de “H-spread” (ou ignorar o elemento e continuar com a lição). Tente o exercício introduzido, ou digite em seu próprio exercício. Em seguida, clique no botão e role para baixo para “encontrar o intervalo interquartil (h-Spread)” para comparar a sua resposta com a de Mathway.
por favor aceite cookies de “preferências” para activar este elemento.
(clique em “toque para ver os passos” a serem dados diretamente ao site Mathway para uma atualização paga.)
Uma vez que você está confortável encontrar o IQR, você pode passar a localizar os valores anómalos, se houver.
-
Encontre os valores anómalos, se houver, para o seguinte conjunto de dados:
10.2, 14.1, 14.4. 14.4, 14.4, 14.5, 14.5, 14.6, 14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
para descobrir se existem alguns casos anómalos, eu primeiro tenho que encontrar o IQR. Existem quinze pontos de dados, por isso a mediana será na oitava posição:
(15 + 1) ÷ 2 = 8
Depois Q2 = 14, 6.
existem sete pontos de dados em ambos os lados da mediana. As duas metades são:
10, 2, 14, 1, 14, 4. 14, 4, 14, 4, 14, 5, 14, 5
…e:
14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
Q1 é o quarto valor na lista, sendo o valor médio da primeira metade da lista; e Q3 é o décimo segundo valor, sendo th valor médio da segunda metade da lista:
Q1 = 14.4
Q3 = 14.9
em Seguida, o IQR é dada por:
IQR = 14.9 – 14.4 = 0.5
Outliers será quaisquer pontos abaixo de Q1 – 1.5 ×IQR = 14.4 – 0.75 = 13.65 ou acima de Q3 + 1.5×IQR = 14.9 + 0.75 = 15.65.
em Seguida, os outliers são:
10.2, 15.9, e 16,4
Conteúdo Continua Abaixo
Os valores de Q1 – 1.5×IQR e T3 + 1.5×IQR são as ” cercas “que marcam os valores” razoáveis ” dos valores mais estranhos. Os anómalos estão fora das cercas.
Se a sua atribuição o leva a considerar não só valores anómalos mas também “valores extremos”, então os valores para Q1 – 1.5×IQR e Q3 + 1.5×IQR são as vedações “interiores” e os valores para Q1 – 3×IQR e Q3 + 3×IQR são as vedações “exteriores”.
os valores anómalos (marcados com asteriscos ou pontos abertos) situam-se entre as vedações interior e exterior e os valores extremos (marcados com o símbolo que não usou para os valores anómalos) situam-se fora das vedações exteriores.
A propósito, seu livro pode se referir ao valor de “1.5×IQR” como sendo um “passo”. Então os anómalos serão os números que estão entre um e dois passos das dobradiças, e o valor extremo serão os números que estão a mais de dois passos das dobradiças.olhando novamente para o exemplo anterior, as cercas externas seriam de 14.4 – 3×0.5 = 12.9 e 14.9 + 3×0.5 = 16.4. Uma vez que o 16.4 está em cima da cerca exterior superior, isso seria considerado apenas um valor fora do normal, e não um valor extremo. Mas o 10.2 está completamente abaixo da cerca externa inferior, por isso o 10.2 seria um valor extremo.
Afiliado
Afiliado
a Sua calculadora gráfica pode ou pode não indicar se uma caixa-e-bigodes inclui outliers. Por exemplo, o problema acima inclui os pontos 10.2, 15.9 e 16.4 como valores anómalos. Uma configuração na minha calculadora de gráficos dá o simples gráfico de caixa-e-whisker que usa apenas o resumo de cinco números, de modo que os valores mais distantes são mostrados como sendo os pontos finais dos bigodes:

Um diferente calculadora definição dá-caixa-e-bigodes com valores atípicos, especialmente marcado (neste caso, com uma simulação de um ponto), e o whiskers vai somente até o maior e o menor valores que não são discrepantes:

a Minha calculadora não faz distinção entre os outliers e valores extremos. O teu também pode não. Verifique o manual do seu dono agora, antes do próximo teste.
Se estiver a usar a sua calculadora de gráficos para ajudar com estes gráficos, certifique-se que sabe qual a configuração que é suposto estar a usar e o que os resultados significam, ou a calculadora pode dar-lhe uma resposta perfeitamente correcta mas “errada”.
-
Encontre os valores anómalos e extremos, se houver, para o seguinte conjunto de dados, e desenhe a parcela de caixa e whisker. Marque quaisquer valores anómalos com um asterisco e quaisquer valores extremos com um ponto aberto.
21, 23, 24, 25, 29, 33, 49
Publicidade
Para encontrar os outliers e valores extremos, eu primeiro tenho que encontrar o IQR. Desde há sete valores na lista, a mediana é o quarto valor, assim:
Q2 = 25
A primeira metade da lista é:
21, 23, 24
…então Q1 = 23; o segundo tempo é:
29, 33, 49
…então Q3 = 33. Então o QI é dado por:
IQR = 33 – 23 = 10
Os outliers será quaisquer valores abaixo:
23 – 1.5×10 = 23 – 15 = 8
…ou acima de:
33 + 1.5×10 = 33 + 15 = 48
Os valores extremos serão os abaixo:
23 – 3×10 = 23 – 30 = -7
…ou superior:
33 + 3×10 = 33 + 30 = 63
assim eu tenho um outlier em 49 mas sem valores extremos. Não vou ter um bigodes de topo no meu enredo porque o Q3 também é o mais alto não-outlier. Então o meu enredo parece-se com isto.:
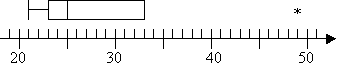
deve-se notar que os métodos, Termos e regras descritos acima são o que eu ensinei e o que eu mais comumente vi ensinado. No entanto, seu curso pode ter regras específicas diferentes, ou sua calculadora pode fazer cálculos ligeiramente diferentes. Você pode precisar ser um pouco flexível em encontrar as respostas específicas ao seu currículo.
URL: https://www.purplemath.com/modules/boxwhisk3.htm
Página 1Page 2Page 3
Leave a Reply