com o sucesso de bilheteria do filme “Interestelar”, muitas pessoas estão entusiasmadas com as perspectivas de buracos de minhoca como um meio para o transporte interestelar. Embora atualmente não haja evidências de que tais objetos exóticos existam na natureza, é possível que eles possam ser criados artificialmente, talvez a partir de versões da teoria das cordas de dimensões superiores e engenharia da espuma espaço-tempo fundamental. A pesquisa de Wormhole é hoje um assunto emocionante com dezenas de artigos publicados em revistas revisadas por pares todos os anos, mas vale a pena ser lembrado de suas origens-e começa de um lugar surpreendente.em 1915, Albert Einstein publicou a sua Teoria Geral da relatividade, a sua descrição da gravidade que define claramente como os objectos se atraem uns aos outros e afectam o espaço e o tempo à sua volta. Muitos anos mais tarde, o físico americano John Wheeler cunharia a frase “o espaço diz a matéria como se mover, e a matéria diz ao espaço como curvar”. Einstein descreveu a gravidade como uma manifestação da curvatura espaço-tempo. A relatividade geral é uma teoria de campo contínua em contraste com a teoria de partículas da matéria que levou à mecânica quântica.Einstein também esteve envolvido no desenvolvimento da mecânica quântica, a teoria que descreve partículas subatômicas. Mas ele não estava inteiramente satisfeito com suas incertezas inerentes e caráter probabilístico. Então, em 1935, ele trabalhou com Nathan Rosen para produzir uma teoria de campo para elétrons, usando a relatividade geral. Seu artigo foi intitulado “The Particle Problem in the General Theory of Relativity”. Einstein e Rosen estavam investigando a possibilidade de um atomizado teoria de matéria e de energia elétrica, excluindo-se descontinuidades (singularidades) em campo, fez uso de nenhum outro variáveis diferente da descrição (métrica) de relatividade geral e a teoria eletromagnética de Maxwell. Uma das consequências foi que a partícula carregada mais elementar foi encontrada para ser uma de massa zero.no final, o que eles produziram foi algo bastante original. Eles começaram com as equações para um esfericamente simétrica distribuição de massa, já usado para buracos negros, e conhecido como a solução de Schwarzschild,

$$ds^2 = -\dfrac{1}{1-2m/r}dr^2 – r^2(d\theta^2+\sin^2\theta d\phi^2) + (1-2m/r)dt^2$$

onde \(ds^2\) é a métrica e \(m=GM/c^2\) com coordenadas esféricas \((r,\theta,\phi)\) com \(t\).

eles realizaram uma transformação coordenada para remover a região contendo a singularidade da curvatura, uma descontinuidade na curvatura do espaço implícita por buracos negros e fenômenos semelhantes. A singularidade em \(r=2m\) foi removido pela transformação de coordenadas \(u^2 = r – 2\), resultando em uma solução final,

$$ds^2 = -4(u^2 + 2m)du^2 – (u^2 + 2m)^2 d\Omega^2 + \dfrac{u^2}{u^2 + 2m} dt^2$$

onde \(d\Omega^2 = d\theta^2 + \sin^2\theta d\phi^2\). esta solução foi uma representação matemática do espaço físico por um espaço de duas folhas assintoticamente planas conectadas por uma ponte ou um wormhole Schwarzschild com uma ‘garganta’. Isto conecta as duas folhas e, por analogia, duas partes separadas do universo real, tridimensional. A figura 1 mostra o espaço em torno do wormhole, com o espaço acima e abaixo tornando-se Plano nas “bordas” enquanto você zoom para o infinito.

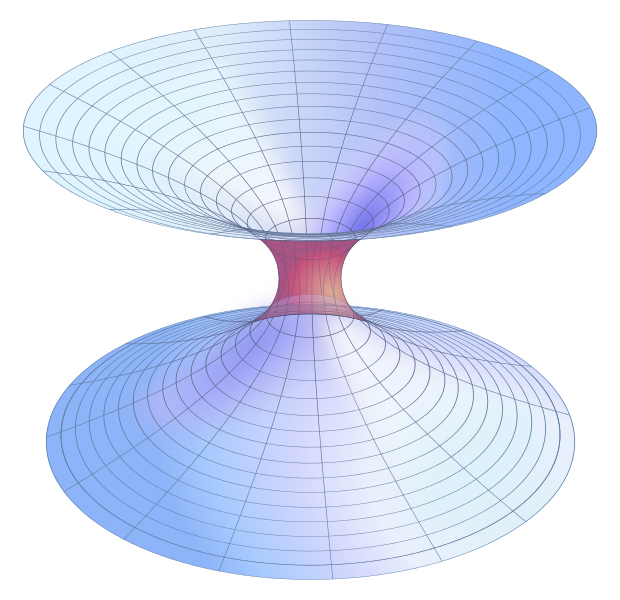
Agora, isso não foi um traversable buraco de minhoca, para que tivemos de aguardar a chegada de físicos John Wheeler na década de 1950 e Kip Thorne, na década de 1980. Em 1987, com o encorajamento de Carl Sagan para o seu romance “Contato” (mais tarde, um longa-metragem), Thorne e seu colega Michael Morris foram capazes de construir uma descrição matemática, uma métrica, para descrever um esfericamente simétrica e estática do buraco de minhoca com um real, finito, circunferência. Isto teve uma coordenada diminuindo do infinito negativo-para fora em espaço minimamente curvado — para um valor mínimo onde a garganta estava localizada, e, em seguida, aumentando da garganta para o infinito positivo-em um espaço minimamente curvado diferente. Esta solução tem a característica distintiva de não ter horizonte de eventos — ao contrário de um buraco negro. The Thorne and Morris paper was titled “Wormholes in Space-time and their use for Interestellar Travel: a Tool for Teaching General Relativity”. Este artigo ajudou a estabelecer a pesquisa de wormhole como nova área de pesquisa acadêmica.

desde então, muitos artigos foram publicados, e de fato pesquisas astronômicas foram realizadas, examinando as estrelas e galáxias mais distantes em busca de buracos de minhoca naturais. Nenhum foi identificado ainda, mas lembre — se da origem deste campo de pesquisa-a Ponte Einstein-Rosen não era um wormhole perceptível, e não era intenção do autor produzir um, mas eles produziram a primeira descrição matemática de um wormhole. Eles devem ser lembrados por isso. A investigação científica produz frequentemente algo bastante inesperado, com implicações que ultrapassam largamente as intenções originais dos investigadores.Kelvin F. Desde que este artigo foi publicado, a nossa revista, Principium, publicou duas edições (edições 9 & 10) onde discutimos wormholes e a Ponte Einstein-Rosen em mais detalhes. Estas questões também detalham o Simpósio de um dia sobre “buracos de minhoca interestelares: física e realização prática” organizado pela iniciativa para estudos interestelares em colaboração com a sociedade interplanetária Britânica.