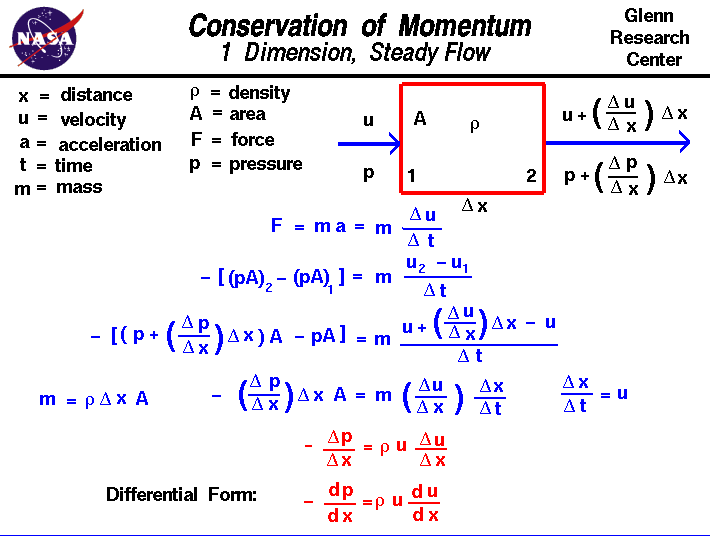
zachowanie pędu jest fundamentalnym pojęciem fizycznym, obejmującym ochronę energii i ochronę masy.Pęd definiuje się jako masę obiektu pomnożoną przez prędkość obiektu.Zachowanie pędu stwierdza, że w niektórych obszarach problemowych wielkość pędu pozostaje stała;pęd nie jest ani tworzony, ani niszczony, a jedynie zmieniany poprzez działanie sił, jak opisuje to Newton.Radzenie sobie z momentem jest trudniejsze niż radzenie sobie z masą i energią, ponieważ „mamentum” jest ilościowe, zachowując zarówno wielkość, jak i kierunek. Pęd jest zachowany we wszystkich trzech kierunkach jednocześnie. Jest to jeszcze trudniejsze, gdy mamy do czynienia z Agą, ponieważ siły w jednym kierunku mogą wpływać na pęd w innym kierunku z powodu zderzeń wielu cząsteczek.Na tym slajdzie przedstawimy bardzo, bardzo uproszczony problem przepływu, w którym właściwości zmieniają się tylko w jednym kierunku.Problem jest dodatkowo uproszczony przez rozważenie stałego przepływu, który nie zmienia się z czasem i przez ograniczenie sił tylko do tych, które są związane z thepressure.Be świadomość, że rzeczywiste problemy z przepływem są znacznie bardziej złożone niż w tym prostym przykładzie.

rozważmy przepływ gazu przez dziedzinę, w której właściwości przepływu zmieniają się w jednym kierunku, który nazwiemy”x”. Gaz wchodzi do stacji domainat 1 z pewną prędkością u, a część pand ciśnienia wychodzi na stację 2 z inną wartością prędkości i ciśnienia. Dla uproszczenia przyjmiemy, że gęstość r pozostaje stała w obrębie domeny i że obszar a, przez który przepływa Gaz, również pozostaje stały. Położenie stacji 1 i 2 jest rozdzielone przez odległość zwaną del x. (Delta to mały trójkąt na suwaku i jest grecką literą „d”. Matematycy często używają tego symbolu do oznaczenia zmiany lub zmiany wielkości. Czcionka Web print nie obsługuje greckich liter, więc po prostu nazwiemy ją „del”.) Zmiana z odległością jest określana jako gradient, aby uniknąć pomyłki ze zmianą z czasem, która jest nazywana szybkością.Gradient prędkości jest oznaczany przez del u / del x; zmiana prędkości na zmianę odległości. Więc na stacji 2, prędkość jest podana przez prędkość 1 plus gradient razy odległość.

podobne wyrażenie daje wyjście:

drugie prawo ruchu Newtona stanowi, że siła F jest równa zmianie pędu w stosunku do czasu. Dla obiektu o stałej masie zmniejsza się to do masy razy przyspieszenie a.An przyspieszenie to zmiana prędkości ze zmianą czasu (del u / del t). Następnie:

siła w tym problemie wynika z gradientu ciśnienia. Ponieważ ciśnienie jest siłą na jednostkę powierzchni, Siła netto na naszą dziedzinę płynów jest ciśnieniem razy obszar przy wejściu minus ciśnienie razy obszar przy wejściu.

znak minus na początku tego wyrażenia jest używany, ponieważ gazy przemieszczają się z obszaru wysokiego ciśnienia do obszaru niskiego ciśnienia; jeśli ciśnienie wzrośnie Z X, prędkość spadnie. Zamiana naszych wyrażeń na prędkość i ciśnienie:

Uprość:

zauważając, że (del x / del T) jest prędkością, a masa jest gęstością r razy objętość (powierzchnia razy del x):

uprość:

del P / del x I del u / del x reprezentują gradienty ciśnienia i prędkości.Jeśli Zmniejszymy naszą domenę do rozmiarów różniczkowych, to te gradienty staną się różniczkami:

jest to jednowymiarowa, stała postać Equation.It warto zauważyć, że spadek ciśnienia płynu (termin po lewej stronie) jest proporcjonalny zarówno do wartości prędkości, jak i gradientu prędkości.Rozwiązanie tego równania pędu daje nam postać dynamicznego nacisku, który pojawia się w równaniu Bernoulliego.

Działalność:
wycieczki z przewodnikiem

• podstawowe równania dynamiki płynów:

Nawigacja ..

Przewodnik dla początkujących Strona główna