w mechanice klasycznejedytuj

w nierelatywistycznej mechanice klasycznej układ zamknięty jest układem fizycznym, który nie wymienia żadnej materii ze swoim otoczeniem i nie podlega żadnej sile sieci, której źródło jest zewnętrzne wobec układu. Układ zamknięty w mechanice klasycznej byłby odpowiednikiem układu izolowanego w termodynamice. Systemy zamknięte są często stosowane w celu ograniczenia czynników, które mogą mieć wpływ na wyniki konkretnego problemu lub eksperymentu.

w termodynamiceedytuj

właściwości układów izolowanych, zamkniętych i otwartych w wymianie energii i materii.

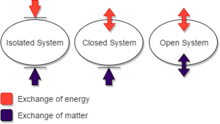
w termodynamice układ zamknięty może wymieniać energię (jako ciepło lub pracę), ale nie ma znaczenia, z jego surroundings.An odizolowany system nie może wymieniać ciepła, pracy ani materii z otoczeniem, podczas gdy otwarty system może wymieniać energię i materię. (Ten schemat definicji terminów nie jest jednolicie stosowany, chociaż jest wygodny dla niektórych celów. W szczególności niektórzy autorzy używają „systemu zamkniętego”, gdzie używa się tutaj „systemu izolowanego”.)

dla układu prostego, posiadającego tylko jeden typ cząstki (atom lub cząsteczkę), układ zamknięty oznacza stałą liczbę cząstek. Jednak w przypadku układów, które przechodzą reakcję chemiczną, mogą występować różnego rodzaju cząsteczki generowane i niszczone w procesie reakcji. W tym przypadku fakt, że układ jest zamknięty, wyraża się stwierdzeniem, że całkowita liczba każdego atomu pierwiastka jest zachowana, bez względu na to, jakiego rodzaju cząsteczka może być częścią. Matematycznie:

∑ j = 1 m a i j n j = b i {\displaystyle \sum _{j=1}^{m}a_{ij}n_{j}=b_{i}}

gdzie n j {\displaystyle n_{j}}

to liczba cząsteczek typu J, A i j {\displaystyle a_{IJ}}

to liczba atomów pierwiastka i {\displaystyle i}

w cząsteczce J {\displaystyle j}

i B i {\displaystyle b_{i}}

jest całkowita liczba atomów pierwiastka i {\displaystyle i}

w układzie, która pozostaje stała, ponieważ układ jest zamknięty. Będzie jedno takie równanie dla każdego innego elementu w układzie.

w termodynamice układ zamknięty jest ważny dla rozwiązywania skomplikowanych problemów termodynamicznych. Umożliwia eliminację niektórych czynników zewnętrznych, które mogłyby zmienić wyniki eksperymentu lub problemu, upraszczając go w ten sposób. Układ zamknięty może być również stosowany w sytuacjach, w których równowaga termodynamiczna jest wymagana do uproszczenia sytuacji.

w fizyce kwantowejedytuj

to równanie, zwane równaniem Schrödingera, opisuje zachowanie izolowanego lub zamkniętego układu kwantowego, czyli z definicji układu, który nie zamienia informacji (tj. energii i / lub materii) z innym układem. Jeśli więc układ izolowany znajduje się w jakimś stanie czystym |ψ(t) ∈ H w czasie t, gdzie H oznacza przestrzeń Hilberta układu, To czasowa ewolucja tego stanu (pomiędzy dwoma kolejnymi pomiarami).

i ℏ ∂ ∂ t ψ ( r , t ) = H ^ ψ ( r , t) {\displaystyle i \ hbar {\frac {\partial }{\partial t}} \ Psi \ Left(\mathbf {r} ,t\right)={\hat {H}}\Psi \Left(\mathbf {r} ,t\right)\,\!}