Wykres nierówności liniowej w jednej zmiennej jest linią liczbową. Użyj otwartego koła dla < I > I zamkniętego koła dla ≤ i ≥.

wykres dla x > -3

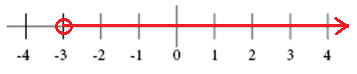
wykres dla X ≥ 2

nierówności, które mają takie same rozwiązania nazywane są równoważnymi. Istnieją własności nierówności, jak również były własności równości. Wszystkie poniższe właściwości są również prawdziwe dla nierówności obejmujących ≥ i ≤.

właściwość dodawania nierówności mówi, że dodanie tej samej liczby do każdej strony nierówności daje równoważną nierówność

$$If \: x>y,\: then\: x+z>y+z$$

$$If\: x<y,\: then\: X+z<y + z$$

właściwość odejmowania nierówności mówi nam, że odejmowanie tej samej liczby z obu stron nierówności daje równoważną nierówność.

$$If \: x>y,\: then\: x-z>y-z$$

$$If\: x<y,\: then\: x-z<Y-Z$$

właściwość mnożenia nierówności mówi nam, że mnożenie po obu stronach nierówności z liczbą dodatnią daje równoważną nierówność.

$$If \: x > y \: i\: z>0,\: then\: xz>yz$$

$$If\: x<y\: and\: z>0,\: następnie\: XZ<YZ$$

mnożenie po każdej stronie nierówności z liczbą ujemną z drugiej strony nie daje równorzędnej nierówności, chyba że również odwrócimy kierunek symbolu nierówności

$$if \: X>y \: i\: z<0,\: then\: XZ<YZ$$

$$if\: X<y\: i\: z <0,\: then\: xz>yz$$

to samo dotyczy własności dzielenia nierówności.

podział obu stron nierówności z liczbą dodatnią daje nierówność równoważną.

$$If \: x>y \: and\: z>0,\: then\: \frac{x}{z}>\frac{y}{z}$$

$$If\: x<Y\: and\: z>0,\: then\: \frac{x}{z}< \ frac{y}{z}$$

i podział po obu stronach nierówności z liczbą ujemną daje nierówność równoważną, jeśli symbol nierówności jest odwrócony.

$$If \: x>y \: and\: z<0,\: then\: \frac{x}{z}<\frac{y}{z}$$

$$If\: x<Y\: and\: z<0,\: then\: \frac{x}{z}>\frac{y}{z}$$ $

aby rozwiązać wieloetapową nierówność, wykonujesz to samo, co podczas rozwiązywania równań wieloetapowych. Weźmy jedną rzecz w czasie najlepiej zaczynając od odizolowania zmiennej od stałych. Podczas rozwiązywania wieloetapowych nierówności ważne jest, aby nie zapomnieć o odwróceniu znaku nierówności podczas mnożenia lub dzielenia liczbami ujemnymi.

przykład

Rozwiąż nierówność

$$-2\left (x + 3 \right )<10$$