Rational Exponents
Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
wprowadzenie
pierwiastki kwadratowe są najczęściej zapisywane przy użyciu znaku radykalnego, takiego jak ten, ![]() . Ale jest inny sposób reprezentowania zakorzenienia. Można użyć wykładników racjonalnych zamiast rodnika. Wykładnik racjonalny to wykładnik będący ułamkiem. Na przykład
. Ale jest inny sposób reprezentowania zakorzenienia. Można użyć wykładników racjonalnych zamiast rodnika. Wykładnik racjonalny to wykładnik będący ułamkiem. Na przykład ![]() można zapisać jako
można zapisać jako ![]() .
.
nie wyobrażasz sobie podniesienia liczby do wykładnika racjonalnego? Być może trudno się do nich przyzwyczaić, ale racjonalne wykładniki mogą pomóc w uproszczeniu niektórych problemów. Zbadajmy związek między wykładnikami racjonalnymi (ułamkowymi) a rodnikami.
przepisywanie wyrażeń radykalnych za pomocą wykładników racjonalnych
rodniki i wykładniki ułamkowe są alternatywnymi sposobami wyrażania tego samego. Widzieliście już, jak pierwiastki kwadratowe mogą być wyrażone jako wykładnik potęgi jednej połowy.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
4 |
|
|
|
5 |
|
|
|
10 |
Let’s look at some more examples, but this time with cube roots. Pamiętaj, że podstawianie liczby podnosi ją do potęgi trzech. Zauważ, że w tych przykładach, mianownikiem wykładnika racjonalnego jest Liczba 3.
|
Radical Form |
Exponent Form |
Integer |
|
|
|
2 |
|
|
|
5 |
|
|
|
10 |
These examples help us model a relationship between radicals and wykładniki racjonalne: mianowicie, że n-ty pierwiastek liczby można zapisać jako ![]() lub
lub ![]() .
.
|
Radical Form |
Exponent Form |
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
When faced with an wyrażenie zawierające wykładnik wymierny, można przepisać za pomocą rodnika. W powyższej tabeli zwróć uwagę, jak mianownik wykładnika racjonalnego określa indeks pierwiastka. Tak więc wykładnik ![]() przekłada się na pierwiastek kwadratowy, wykładnik
przekłada się na pierwiastek kwadratowy, wykładnik ![]() przekłada się na piąty pierwiastek lub
przekłada się na piąty pierwiastek lub ![]() , a
, a ![]() przekłada się na ósmy pierwiastek lub
przekłada się na ósmy pierwiastek lub ![]() .
.
|
Example |
||
|
Problem |
Write |
|
|
|
The radical form |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Express |
|
|
|
przepisz wyrażenie z wykładnikiem ułamkowym jako rodnikiem. Mianownik ułamka określa pierwiastek, w tym przypadku pierwiastek sześcianu. nawiasy w |
|
|
odpowiedź |
|
|
pamiętaj, że wykładniki odnoszą się tylko do ilości bezpośrednio po ich lewej stronie, chyba że użyto symbolu grupowania. Poniższy przykład wygląda bardzo podobnie do poprzedniego z jedną ważną różnicą—nie ma nawiasów! Zobacz, co się dzieje.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the expression with the fractional exponent as a radical. Mianownik ułamka określa pierwiastek, w tym przypadku pierwiastek sześcianu. wykładnik odnosi się tylko do części wyrażenia bezpośrednio po lewej stronie wykładnika, w tym przypadku x, ale nie do 2. |
|
|
Answer |
|
|
Rewriting Expressions with Rational Exponents Using Radicals
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
|
Example |
||
|
Problem |
Express |
|
|
|
Rewrite the radical using a rational exponent. The root determines the fraction. W tym przypadku indeks pierwiastka wynosi 3, więc wykładnik racjonalny będzie równy ponieważ 4 jest poza rodnikiem, nie jest uwzględniany w symbolu grupowania, a wykładnik nie odnosi się do niego. |
|
|
Answer |
|
|
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 |
Find the square root of both the coefficient and the variable. |
|
|
odpowiedź |
|
|
wykładniki wymierne z licznikami innymi niż jeden
wszystkie liczniki dla wykładników ułamkowych w powyższych przykładach były 1. Możesz użyć wykładników ułamkowych, które mają liczniki inne niż 1, aby wyrazić pierwiastki, jak pokazano poniżej. Zauważyłeś jakieś wzory w tej tabeli?
|
Radical |
Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
|
aby przepisać rodnik za pomocą wykładnika ułamkowego, moc, do której jest podniesiony rodnik, staje się licznikiem, a pierwiastek staje się mianownikiem.
zapisanie wykładników ułamkowych
dowolny pierwiastek w postaci![]() można zapisać za pomocą wykładnika ułamkowego w postaci
można zapisać za pomocą wykładnika ułamkowego w postaci![]() .
.
zależność między![]() I
I![]() działa również dla wykładników racjonalnych, które mają licznik 1. Na przykład radykalny
działa również dla wykładników racjonalnych, które mają licznik 1. Na przykład radykalny ![]() może być również zapisany jako
może być również zapisany jako ![]() , ponieważ każda liczba pozostaje tą samą wartością, jeśli zostanie podniesiona do pierwszej potęgi. Możesz teraz zobaczyć, skąd pochodzi licznik 1 w równoważnej formie
, ponieważ każda liczba pozostaje tą samą wartością, jeśli zostanie podniesiona do pierwszej potęgi. Możesz teraz zobaczyć, skąd pochodzi licznik 1 w równoważnej formie ![]() .
.
upraszczanie wyrażeń radykalnych za pomocą wykładników racjonalnych i praw wykładników
przyjrzyjmy się teraz kilku wyrażeniom radykalnym i zobaczmy, jak je uprościć. Oto radykalne wyrażenie, które wymaga uproszczenia, ![]() .
.
jedną z metod upraszczania tego wyrażenia jest dzielenie i wyciąganie grup a3, jak pokazano poniżej w tym przykładzie.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite by factoring out cubes. |
|
|
|
Write each factor under its own radical and simplify. |
|
|
odpowiedź |
|
|
można również uprościć to wyrażenie, myśląc o rodniku jako wyrażeniu o wykładniku racjonalnym i stosując zasadę, że każdy Rodnik w postaci ![]() można zapisać używając wykładnika ułamkowego w postaci
można zapisać używając wykładnika ułamkowego w postaci ![]() .
.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using a rational exponent. |
|
|
|
Simplify the exponent. |
|
|
Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
obie metody upraszczania dały ten sam wynik, a2. W zależności od kontekstu problemu, może być łatwiej użyć jednej lub drugiej metody, ale na razie zauważysz, że udało ci się uprościć to wyrażenie szybciej przy użyciu wykładników racjonalnych niż przy użyciu metody „pull-out”.
spróbujmy innego przykładu.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the radical using rational exponents. Use the rules of exponents to simplify the expression. |
|
|
|
||
|
|
Change the expression with the wykładnik racjonalny wraca do formy radykalnej. |
|
|
odpowiedź |
|
|
ponownie alternatywną metodą jest praca nad upraszczaniem pod pierwiastkiem za pomocą faktoringu. Na przykład, który właśnie rozwiązałeś, wygląda to tak.
|
Example |
||
|
Problem |
Simplify. |
|
|
|
Rewrite the expression. |
|
|
|
Factor each radicand. |
|
|
|
Simplify. |
|
|
Answer |
|
|
Which of the expressions below is equal to the expression ![]() when written using a rational exponent?
when written using a rational exponent?
a) ![]()
B) ![]()
C) ![]()
D) ![]()
spróbujmy bardziej skomplikowanego wyrażenia, ![]() . Wyrażenie to ma dwie zmienne, ułamek i pierwiastek. Zróbmy to krok po kroku i zobaczmy, czy użycie wykładników ułamkowych pomoże nam to uprościć.
. Wyrażenie to ma dwie zmienne, ułamek i pierwiastek. Zróbmy to krok po kroku i zobaczmy, czy użycie wykładników ułamkowych pomoże nam to uprościć.
zacznijmy od uproszczenia mianownika, ponieważ tutaj znajduje się znak rodnika.
|
Example |
|||
|
Problem |
Simplify. |
||
|
|
Separate the factors in the denominator. |
||
|
|
Take the cube root of 8, which is 2. |
||
|
|
|
Rewrite the radical using a fractional exponent. |
|
|
|
Rewrite the fraction as a series of factors in order to cancel factors (see next step). |
||
|
|
Simplify the constant and c factors. |
||
|
|
Use the rule of negative exponents, n-x= |
||
|
|
Combine the b factors by adding the exponents. |
||
|
|
Change the expression with the fractional exponent back to radical form. Zgodnie z konwencją wyrażenie nie jest zwykle uważane za uproszczone, jeśli ma wykładnik ułamkowy lub Rodnik w mianowniku. |
odpowiedź |
|
cóż, trochę to trwało, ale się udało. Zastosowałeś to, co wiesz o wykładnikach ułamkowych, ujemnych wykładnikach i regułach wykładników, aby uprościć wyrażenie.
podsumowanie
radykał może być wyrażony jako wyrażenie z wykładnikiem ułamkowym zgodnie z konwencją ![]() . Przepisywanie rodników za pomocą wykładników ułamkowych może być przydatne w upraszczaniu niektórych wyrażeń rodnikowych. Podczas pracy z wykładnikami ułamkowymi należy pamiętać, że wykładniki ułamkowe podlegają wszystkim tym samym zasadom, co inne wykładniki, gdy pojawiają się w wyrażeniach algebraicznych.
. Przepisywanie rodników za pomocą wykładników ułamkowych może być przydatne w upraszczaniu niektórych wyrażeń rodnikowych. Podczas pracy z wykładnikami ułamkowymi należy pamiętać, że wykładniki ułamkowe podlegają wszystkim tym samym zasadom, co inne wykładniki, gdy pojawiają się w wyrażeniach algebraicznych.
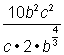
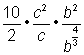
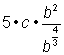
Leave a Reply