Najpiękniejsze i najważniejsze równania matematyczne
Matematyka to bardziej maraton niż sprint — to długi, powolny i równomierny grind, z rzadkimi momentami przełomu. Mimo to, raz na jakiś czas, dostajemy te cenne „Eureka” chwile, te krótkie linie liter i cyfr, które zmieniają naukę na zawsze. Oto niektóre z najbardziej znanych równań, od starożytnych Greków do współczesnej fizyki.
twierdzenie Pitagorasa (530 p. n. e.)
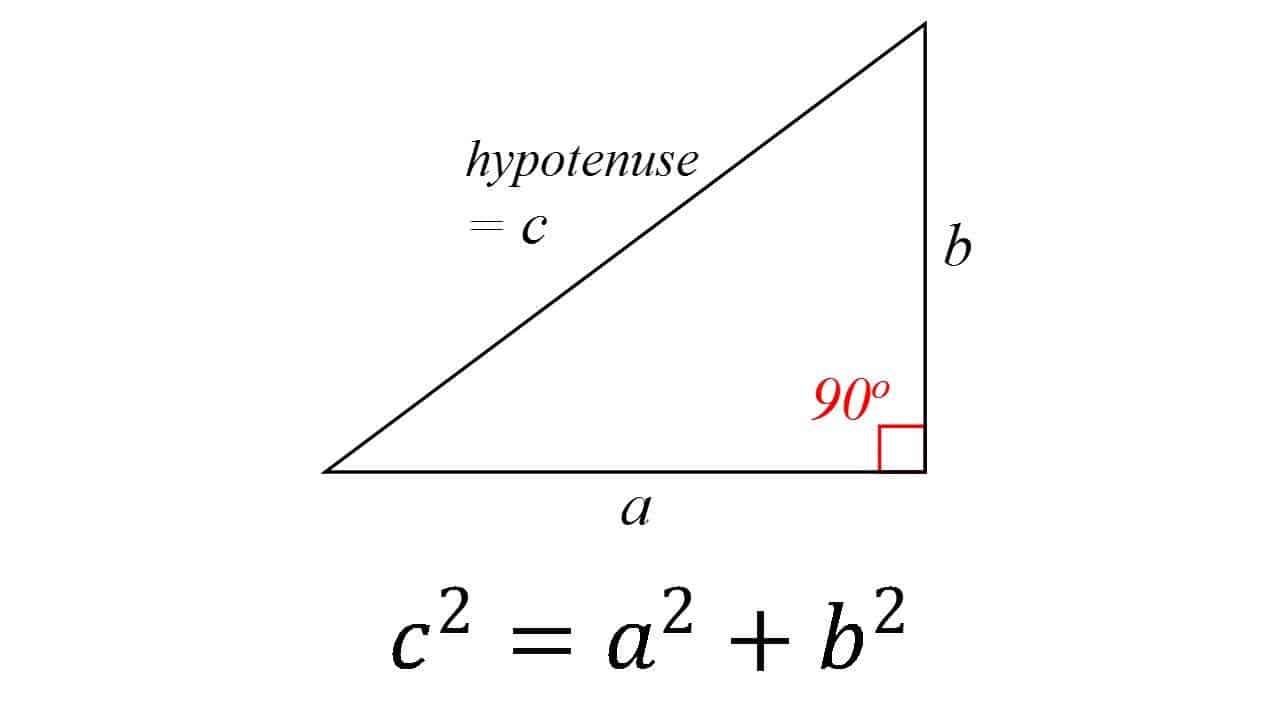
To jest całkiem jeden z filarów fundamentalnych Cała geometria: w trójkącie prostokątnym kwadrat przeciwprostokątnej (bok przeciwległy do kąta prostego)jest równy sumie kwadratów pozostałych dwóch. Teoria ta jest na ogół przypisywana greckiemu matematykowi Pitagorasowi, choć istnieją pewne dowody na to, że matematycy Babilońscy rozumieli formułę. Jest również bardzo możliwe, że twierdzenie było znane przez wielu ludzi, ale był pierwszym, który to udowodnił.
twierdzeniu podano wiele dowodów — prawdopodobnie najwięcej dla dowolnego twierdzenia matematycznego. Są one bardzo zróżnicowane, w tym zarówno dowody geometryczne, jak i algebraiczne, a niektóre pochodzą sprzed tysięcy lat.
Liczby zespolone

włoski matematyk Gerolamo Cardano jest pierwszym znanym, który wprowadził liczby zespolone, nazywając je wówczas „fikcyjnymi”. Jednak matematyczny rozwój ” i ” jako liczby urojonej reprezentującej pierwiastek kwadratowy z -1 przypisuje się Leonhardowi Eulerowi, jednemu z najważniejszych matematyków i naukowców w historii ludzkości.
Liczby zespolone to w zasadzie liczby, które tak naprawdę nie istnieją, ale są bardzo przydatne do wielu obliczeń. Składają się z liczb z częścią rzeczywistą (liczby, które wszyscy znamy) i częścią urojoną (reprezentowaną tutaj przez i) i mają praktyczne zastosowanie w wielu dziedzinach, w tym w fizyce, chemii, biologii, ekonomii, elektrotechnice i statystyce.
logarytmy

Logarytmy są zasadniczo odwrotną funkcją wykładnictwa. Potrzebujesz liczby (N), podstawy (a), a logarytm N w bazie a będzie x, gdzie N równa się a do potęgi x. może się wydawać, że tylko inny sposób zapisu tego samego (i w pewnym sensie jest), ale logarytmy mają niezliczone praktyczne zastosowania, są używane w psychologii, ekonomii i pomiarach wielu zjawisk fizycznych (takich jak pH lub wielkość trzęsienia ziemi).
Logarytmy zostały publicznie przedstawione przez Jana Napiera w 1614 roku, w książce zatytułowanej Mirifici Logarithmorum Canonis Descriptio (opis cudownej reguły logarytmów) — odpowiedni tytuł. Szczególnym przypadkiem logarytmu jest logarytm naturalny-e, gdzie e jest liczbą irracjonalną i transcendentalną w przybliżeniu równą 2.71828182845. W rzeczywistości sama e ma fascynującą historię i imponującą liczbę zastosowań, ale to historia na inny czas.
Rachunek różniczkowy
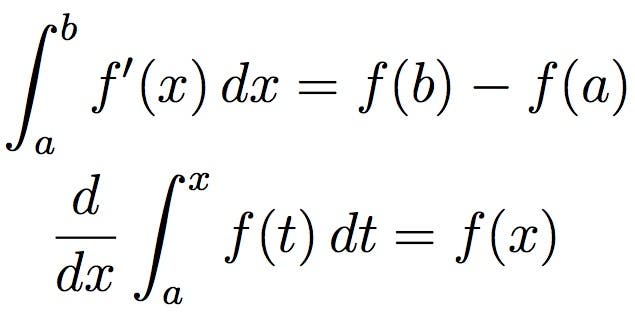
niewiele dziedzin matematyki miało tak duży wpływ jak rachunek różniczkowy. Opracowany w XVII wieku przez Izaaka Newtona i Gottfrieda Wilhelma Leibniza rachunek jest szeroko stosowany w naukach ścisłych, inżynierii i ekonomii. Rachunek zwykle koncentruje się na radzeniu sobie z małymi ilościami, szczególnie nieskończenie małymi ilościami. Przez rachunek różniczkowy można je traktować jako liczby rzeczywiste, nawet jeśli są technicznie nieskończenie małe.
dla prostszej wizualizacji, integracja, przedstawiona powyżej, może być traktowana jako pomiar obszaru pod krzywą, zdefiniowaną przez funkcję.
prawo grawitacji
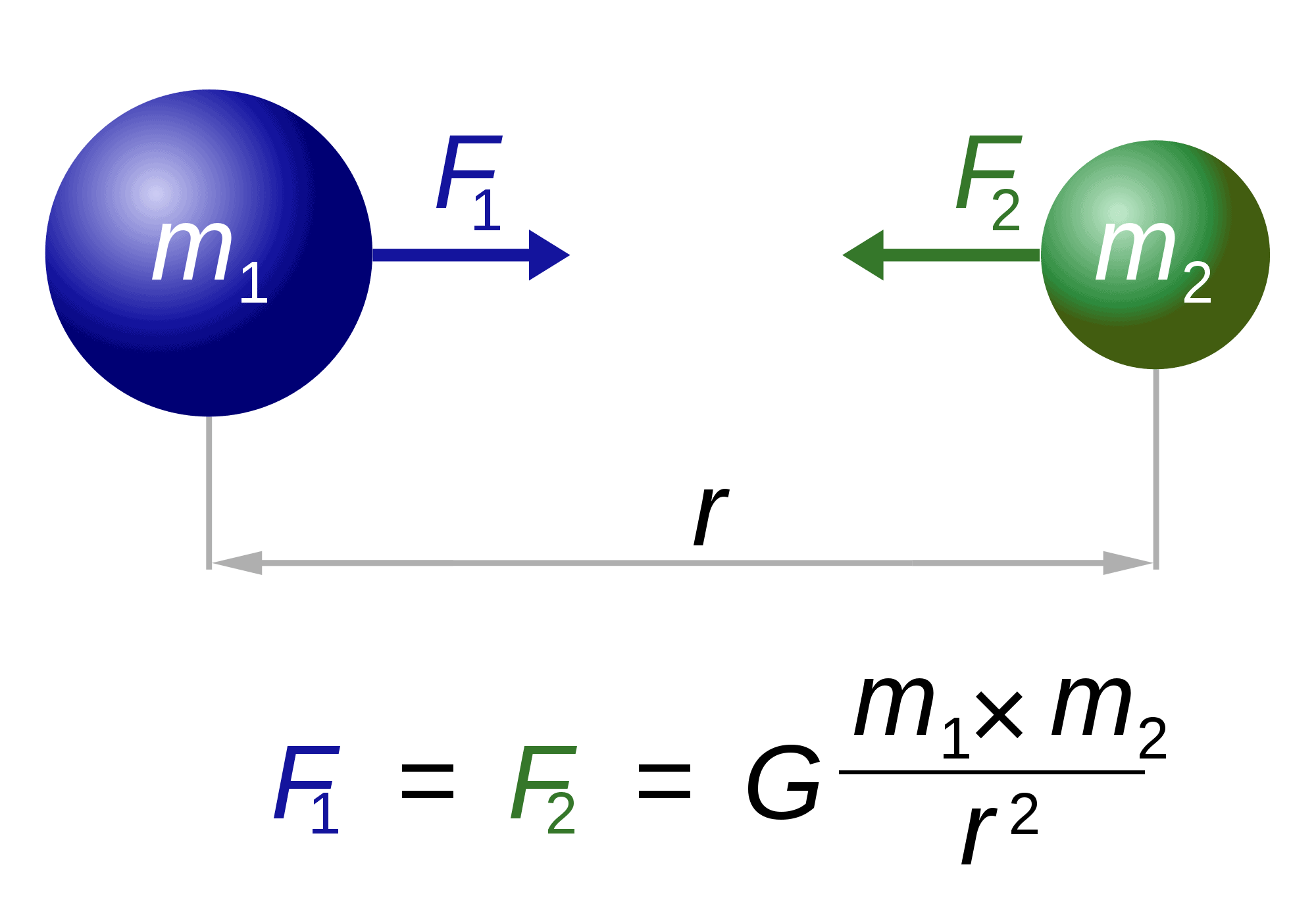
mówiąc o Newtonie, jest również „odpowiedzialny” za jedno z najsłynniejszych i najbardziej spektakularnych równań na świecie: prawo grawitacji.
prawo zasadniczo opisuje, jak dowolne dwa ciała o masach M1 i M2 są przyciągane do siebie. Siła (F1, F2) jest odwrotnie proporcjonalna do kwadratu odległości między nimi (r). Jedynym pozostałym czynnikiem, G, jest stała grawitacyjna. Natura tej stałej pozostaje nieuchwytna.
Ogólna teoria względności

przez prawie 200 lat prawo Newtona określało nasz poziom rozumienia mechaniki. Prace Einsteina w XX wieku przeniosły rzeczy na wyższy poziom — te dwa osiągnięcia wznoszą się na najwyższych piedestałach w świecie fizyki.
ogólna teoria względności jest zasadniczo geometryczną teorią grawitacji, uogólniając teorię Newtona dostarczając ujednoliconego opisu grawitacji jako geometrycznej własności przestrzeni i czasu — lub czasoprzestrzeni. W szczególności Einstein pokazał nie tylko, że istnieje coś takiego jak „czasoprzestrzeń” łącząca trzy wymiary z czwartym wymiarem czasu, ale także pokazał, że ta czasoprzestrzeń może być zakrzywiona przez grawitację, a krzywizna jest bezpośrednio związana z energią i pędem jakiejkolwiek materii i promieniowania.
drugie prawo termodynamiki
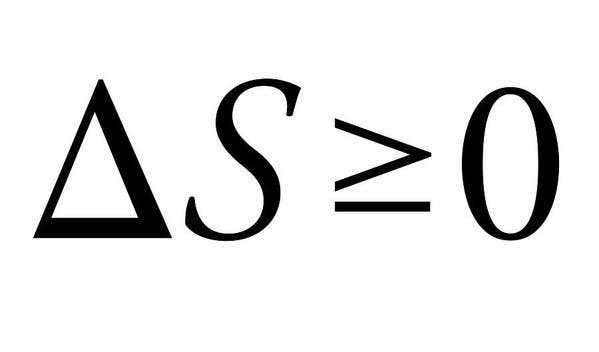
drugie prawo termodynamiki jest powodem, dla którego nie możemy mieć ładnych rzeczy we wszechświecie. Cztery prawa termodynamiki definiują podstawowe wielkości fizyczne (temperaturę, energię i entropię) charakteryzujące układy termodynamiczne. W szczególności drugi wyróżnia się tutaj prostotą, ale absolutnie ogromnymi implikacjami.
prawo zasadniczo stwierdza, że suma entropii oddziałujących ze sobą układów termodynamicznych musi zawsze wzrastać, lub co najwyżej pozostać stała. Kiedy energia zmienia się z jednej formy do drugiej lub Materia porusza się wokół, Entropia (lub zaburzenia) w zamkniętym systemie wzrasta. Wszystkie różnice w temperaturze, ciśnieniu i gęstości mają tendencję do wyrównywania się po pewnym czasie
równania Maxwella
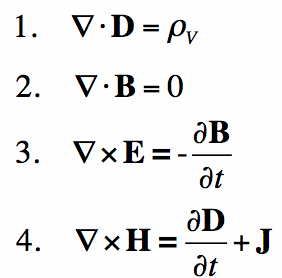
Mówiąc najprościej, równania Maxwella są dla elektromagnetyzmu tym, czym prawo Newtona jest dla mechaniki. Stanowią matematyczne podstawy klasycznego elektromagnetyzmu, klasycznej optyki i obwodów elektrycznych. Są one szeroko stosowane w samym urządzeniu, na którym to czytasz-w zasadzie we wszystkich urządzeniach elektronicznych.
prawa Maxwella opisują, w jaki sposób pola elektryczne i magnetyczne są generowane przez ładunki, prądy i zmiany pól. Znaczącym przełomem było wykazanie, że pola elektryczne i magnetyczne propagują się z prędkością światła.
tożsamość Eulera

wreszcie, jest to prawdopodobnie najbardziej eleganckie równanie, rzecz o najwyższym pięknie, ponieważ obejmuje wszystkie „podstawowe” liczby:
- 0, które jest neutralne dla dodawania i odejmowania;
- 1, które jest neutralne dla mnożenia i dzielenia;
- e, które jest liczbą Eulera (patrz wyżej), podstawą logarytmów naturalnych;
- i jest jednostką urojoną (patrz wyżej); i
- π to pi, stosunek obwodu okręgu do jego średnicy.
znalezienie relacji łączącej wszystkie te liczby jest niczym zapierającym dech w piersiach i wydaje się mało prawdopodobne. Demonstracja nie jest do końca prosta, ale można ją zobaczyć tutaj.
dobrze, że profesor matematyki na Uniwersytecie Stanforda Keith Devlin opisał to równanie, mówiąc, że „jak Szekspirowski SONET, który ujmuje samą istotę miłości, czy obraz, który wydobywa piękno ludzkiej formy, która jest o wiele więcej niż tylko głęboka skóra, równanie Eulera sięga do samych głębi istnienia”
nieczęsto matematyka i fizyka sprowadzają się do prostych i eleganckich równań — ale kiedy to robią, jest to niezły widok.
Leave a Reply