liczby zespolone: wprowadzenie (strona 1 z 3)

sekcje: wprowadzenie, operacje z kompleksami, wzór kwadratowy

do tej pory powiedziano ci, że nie możesz wziąć pierwiastka kwadratowego z liczby ujemnej. To dlatego, że nie miałeś liczb, które były ujemne po ich do kwadratu (więc nie mogłeś „cofnąć się”, biorąc pierwiastek kwadratowy). Każda liczba była dodatnia po tym, jak ją podniosłeś do kwadratu. Więc nie można bardzo dobrze pierwiastek kwadratowy minus i oczekiwać, aby wymyślić coś sensownego.

teraz jednak możesz wziąć pierwiastek kwadratowy z liczby ujemnej, ale wymaga to użycia nowej liczby. Ten nowy numer został wynaleziony(odkryty?) w okresie reformacji. W tamtym czasie nikt nie wierzył, że dla tej nowej liczby znajdzie się jakiekolwiek” rzeczywiste ” użycie, poza ułatwieniem obliczeń związanych z rozwiązywaniem pewnych równań, więc nowa liczba była postrzegana jako liczba pozorowana wymyślona dla wygody.

(ale jak się nad tym zastanowić, to czy wszystkie liczby nie są wynalazkami? To nie tak, że liczby rosną na drzewach! Żyją w naszych głowach. Wymyśliliśmy je wszystkie! Dlaczego nie wymyślić nowego, o ile działa dobrze z tym, co już mamy?)

następnie:

teraz możesz pomyśleć, że możesz to zrobić:

ale to nie ma sensu! Masz już dwie liczby, które są kwadratowe do 1; mianowicie -1 i +1. I już kwadraty do -1. Więc to nie jest rozsądne, że ja również do kwadratu do 1. Wskazuje to na ważny szczegół: Kiedy mamy do czynienia z wyobrażeniami, coś zyskujemy (umiejętność radzenia sobie z negatywami wewnątrz pierwiastków kwadratowych), ale także coś tracimy (niektóre z elastyczności i wygodnych zasad, które mieliśmy do czynienia z pierwiastkami kwadratowymi). W szczególności zawsze musisz najpierw zrobić i-PART!

• Uprość sqrt(-9). Copyright © Elizabeth Stapel 2000-2011 Wszelkie prawa zastrzeżone

(Uwaga: krok, który przechodzi przez trzeci znak „równości” to ” „, a nie „„. I jest poza radykałem.)

• Uprość sqrt (-25).

w swoich obliczeniach będziesz miał do czynienia z i tak jak z x, z wyjątkiem faktu, że x2 to po prostu x2, ale i2 to -1:

• Uprość 2i + 3i.

2i + 3i = (2 + 3)i = 5i

• 16I – 5I.

16i – 5i = (16 – 5)i = 11i

• mnożenie i upraszczanie (3i)(4i).

(3i)(4i) = (3·4)(i·i) = (12) (i2) = (12)(-1) = -12

• mnożyć i upraszczać (i)(2i)(–3i).

(i)(2i)(–3i) = (2 · -3)(i · i · i) = (-6)(i2 · i)

=(-6)(-1 · i) = (-6)(–i) = 6i

zwróć uwagę na ten ostatni problem. W nim widać, że , ponieważ i2 = -1. Kontynuując, otrzymujemy:

Ten wzór potęg, znaków, jedynek i i jest cyklem:

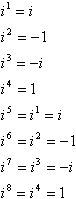
innymi słowy, aby obliczyć dowolną dużą moc i, można przekształcić ją na mniejszą moc przez biorąc najbliższą wielokrotność 4, która nie jest większa od wykładnika i odejmując tę wielokrotność od wykładnika. Na przykład, częstym podchwytliwym pytaniem na testach jest coś w stylu „Uprość i99”, idea jest taka, że spróbujesz pomnożyć i dziewięćdziesiąt dziewięć razy i zabraknie Ci czasu, a nauczyciele dostaną dobry chichot na twój koszt w sali wykładowej. Oto jak działa skrót:

i99 = i96+3 = i(4×24)+3 = i3 = –i

czyli i99 = i3, ponieważ możesz po prostu wyłączyć i96. (96 jest wielokrotnością 4, więc i96 jest po prostu 1, co można zignorować.) Innymi słowy, możesz podzielić wykładnik przez 4 (używając długiego dzielenia), odrzucić odpowiedź i użyć tylko reszty. To da ci część wykładnika, na której ci zależy. Oto kilka przykładów:

• Uprość i17.

i17 = i16 + 1 = i4 · 4 + 1 = i1 = i

i120 = i4 · 30 = i4· 30 + 0 = i0= 1

i64,002 = i64,000 + 2 = i4 · 16,000 + 2 = i2 = –1

Top | 1 | 2 | 3 | Return to Index Next >>