Jason McCormick
profesor nadzwyczajny, Civil & Inżynieria Środowiska, University of Michigan, Ann Arbor, MI, USA

połączenia momentowe wykonane z prostokątnych i kwadratowych pustych sekcji konstrukcyjnych (HSS) otrzymały mniej uwagi w porównaniu z połączeniami HSS do HSS składającymi się z elementów obciążonych osiowo (T, Y, cross i K-połączenia). W większości badań statycznych skupiających się na tych połączeniach rozważano systemy kratownic Vierendeel. Systemy te są często tworzone przez kwadratowe lub prostokątne akordy górne i dolne, które są połączone z kwadratowymi lub prostokątnymi pionowymi prętami (gałęziami) (Rysunek 1). W wyniku tej konfiguracji połączenie akord-web ulega znacznemu zginaniu wraz z obciążeniami ścinającymi i osiowymi i nie jest uważane za połączenie pinowe, jak to zwykle ma miejsce w typowych systemach kratownicowych. Pierwotnie pomyślany w 1896 roku przez Arthura Vierendeela, dopiero gdy opracowano HSS, zaczęto realizować potencjał kratownic Vierendeel (Korol et al. 1977), ale ich użycie wymagało zrozumienia, jak przenosić moment między połączeniami T HSS-to-HSS.

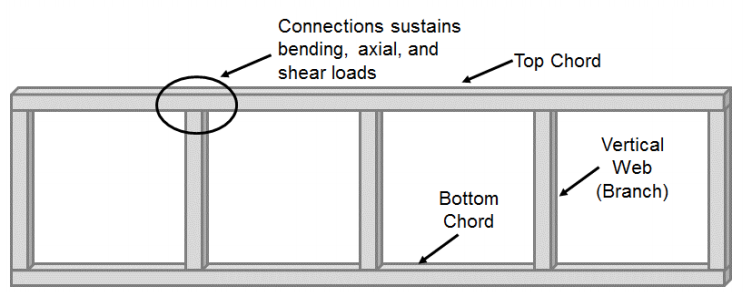
wiele wczesnych badań tych połączeń koncentrowało się na zdolności połączenia do rozwijania pełnej zdolności chwilowej członka oddziału. Jubb i Redwood (1966) wykazali, że gdy odcinek odgałęzienia ma równą szerokość do odcinka akordowego (β=1), można osiągnąć pełną zdolność chwilową członu HSS bez wzmocnienia. W badaniu tym nie uwzględniono jednak potencjalnej utraty pojemności chwilowej spowodowanej obecnością obciążenia osiowego. Z drugiej strony, Korol et al. (1977) wykazał, że połączenia o mniejszej szerokości gałęzi niż akord nie mogą rozwinąć pełnej pojemności chwilowej gałęzi bez wzmocnienia poprzez serię 29 różnych testów połączeń uwzględniających 5 różnych konfiguracji (unreinforced, płyty wzmacniające kołnierz odgałęzienia, usztywnienia kołnierza akordu, haunch i ścięta piramida). Ogólnie rzecz biorąc, wytrzymałość i sztywność nieforsowanych połączeń typu Vierendeel zmniejsza się wraz ze wzrostem współczynnika smukłości akordu (B / t) i zmniejszeniem stosunku szerokości gałęzi do akordu (β). W rezultacie, nieuszkodzone połączenia kratownicowe Vierendeel można uznać za sztywne (tj. poddać minimalnemu względnemu obrotowi między akordem a gałęzią), gdy stosunek szerokości gałęzi do akordu wynosi 1,0, a stosunek smukłości akordu jest niski lub połączenie jest wzmocnione (Packer 1993).

ponieważ maksymalne momenty w tych połączeniach mogą wystąpić przy nadmiernie dużych odkształceniach, przyjęto podejście podobne do tego stosowanego w przypadku osiowo obciążonych kwadratowych i prostokątnych połączeń HSS, gdzie do scharakteryzowania momentu konstrukcyjnego stosuje się ostateczną nośność lub granicę odkształcenia lub obrotu (Wardenier 1982). AISC 360-10 (Rozdział K3) rozważa trzy stany graniczne dla kwadratowych i prostokątnych połączeń T HSS w przypadku statycznego gięcia w płaszczyźnie: plastyfikacja ściany akordowej, lokalne plonowanie ściany bocznej i lokalne plonowanie gałęzi z powodu nierównomiernego rozkładu obciążenia. Uplastycznienie ściany akordu następuje w wyniku tego, że szerokość członu odgałęzionego jest mniejsza niż szerokość akordu (β ≤ 0,85), co wymaga przeniesienia obciążeń rozciągających i ściskających wytwarzanych przez moment zginający przez stosunkowo elastyczną powierzchnię akordu, a nie bezpośrednio na sztywniejsze ściany boczne. Równanie stanu granicznego (równanie AISC 360-10 K3-6) można wyprowadzić z teorii linii uzysku (Rysunek 2):

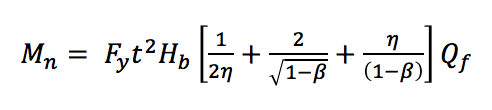
Mn to nominalna Pojemność momentu połączenia, Fy to określona minimalna granica plastyczności akordu, Hb to całkowita wysokość gałęzi, h to parametr długości obciążenia równy wysokości gałęzi podzielonej przez szerokość akordu (zakładając kąt 90o między akordem a członem gałęzi, jak to jest typowe dla Vierendeel kratownice), a QF jest parametrem zmniejszającym pojemność złącza w obecności ściskania osiowego w strunie.

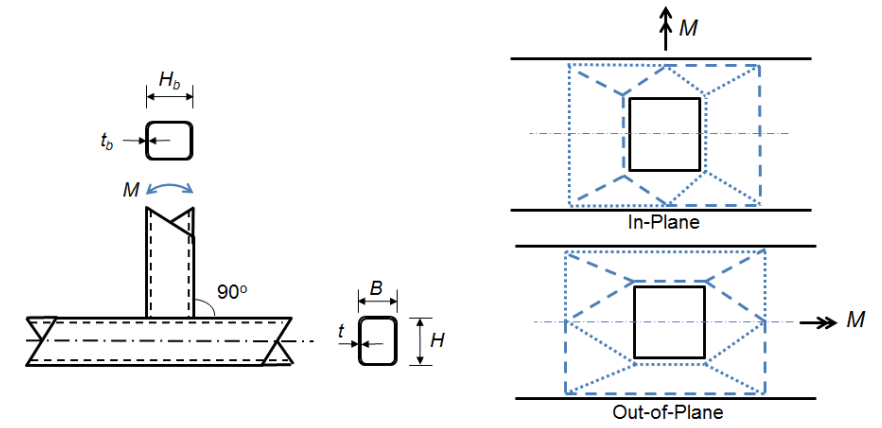
pozostałe dwa stany graniczne są związane z połączeniami, w których szerokość członu odgałęzienia jest równa lub prawie równa szerokości akordu (β > 0.85) oznacza, że obciążenia rozciągające i ściskające opracowane w kołnierzach członu odgałęzionego są przenoszone prawie bezpośrednio na sztywniejsze ścianki boczne akordu. Stan graniczny lokalnego plonowania ściany bocznej (równanie AISC 360-10 K3-7) połączenia T można następnie uzyskać z równania lokalnego plonowania sieci dla skoncentrowanych sił przyłożonych w odległości od końca pręta większej niż jego głębokość (równanie AISC 360-10 J10-2):

Mn = 0.5fyt(Hb + 5T)2
równanie 2

w przypadku lokalnego uzyskiwania odgałęzienia z powodu nierównomiernego rozkładu obciążenia (równanie AISC 360-10 K3-8) w połączeniu T stosuje się podejście efektywnej szerokości w celu zmniejszenia pojemności elementu usztywniającego w celu uzyskania momentu nominalnego zastosowanego przez klamrę:

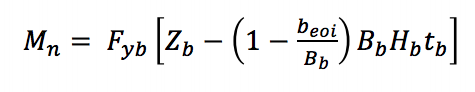
Fyb to określona minimalna granica plastyczności gałęzi, Zb to moduł przekroju z tworzywa sztucznego gałęzi wokół osi zginania, beoi to Efektywna szerokość gałęzi, Bb to Całkowita szerokość gałęzi, a tb to grubość ścianki konstrukcyjnej gałęzi.

ponieważ istnieją ograniczone eksperymentalne dowody na poparcie konkretnych modeli projektowych dla połączeń kratownicowych Vierendeel (połączenia T) w przypadku gięcia poza płaszczyzną, stosuje się analogiczne stany graniczne, jak te dla gięcia w płaszczyźnie (Packer et al. 2010). Jeden dodatkowy Stan graniczny zniekształcenia akordu rozwija się z momentu przyłożonego do akordu przez członka gałęzi w wyniku momentu poza płaszczyzną. Ten moment obrotowy może prowadzić do romboidalnego zniekształcenia akordu. Nominalne równania momentu dla zginania poza płaszczyzną można znaleźć w równaniach AISC 360-10 K3-9, K3-10, K3-11 i K3-12. Równania zarówno w płaszczyźnie i poza płaszczyzną zginania połączeń T są podobne do tych, które zostały przyjęte na arenie międzynarodowej (Packer et al. 2010).

powyższe równania konstrukcyjne zostały wyprowadzone z uwzględnieniem systemów kratownic Vierendeel pod obciążeniami statycznymi. Ostatnie badania (Fadden et al. 2015) rozszerzył tę pracę, aby rozważyć zachowanie kwadratowych i prostokątnych połączeń momentowych Hss-Do-HSS pod dużymi obciążeniami cyklicznymi do stosowania w systemach sejsmicznych momentów sejsmicznych opartych na lampach (ramki pośrednie i specjalne). Taki system wykorzystuje doskonałe właściwości osiowe, zginające i skrętne, wysoki stosunek wytrzymałości do masy oraz architektonicznie przyjemny charakter kwadratowego i prostokątnego HSS. Wysoki opór skrętny może prowadzić do zmniejszenia usztywnienia poprzecznego wiązki, podczas gdy wysoki stosunek wytrzymałości do masy skutkuje niższą masą sejsmiczną. Jednak takie połączenia muszą być w stanie poddać się stabilnemu plastikowemu zawiasowi elementu belki, w którym 80% plastikowej pojemności elementu belki jest utrzymywane do 0,2 rad. (MFW) lub 0,4 rad. (SMF) z Inter-story drift (AISC 341-10). Biorąc pod uwagę, że obecna konstrukcja sejsmiczna systemów ramek momentowych wymaga większości nieelastycznych zachowań występujących w członie wiązki, człon wiązki musi również osiągnąć pełną plastyczną pojemność przed poddaniem się lokalnemu wyboczeniu. Fadden I McCormick (2014a) rozważali zarówno modele eksperymentalne, jak i modele elementów skończonych w celu określenia wymagań ograniczających szerokość-grubość i głębokość-grubość dla HSS w trakcie gięcia, ponieważ te określone w obecnych przepisach sejsmicznych AISC (AISC 341-10) zostały w dużej mierze opracowane w oparciu o testy cyklicznych osiowo obciążonych elementów HSS.

aby określić odpowiednią konfigurację i wymagania dotyczące szczegółów, aby spełnić to zapotrzebowanie na wytrzymałość i ciągliwość, eksperymentalnie przetestowano cztery różne konfiguracje połączeń: dwa bezpośrednio spawane połączenia niezrealizowane (niezrównane i dopasowane) i dwa wzmocnione połączenia (Płyta przelotowa i zewnętrzna Płyta membranowa). We wszystkich połączeniach zastosowano kolumnę HSS 10X10X5/8. Bezpośrednio spawane połączenia wykorzystywały wstępnie kwalifikowane spoiny CJP określone w AWS D1.1 (2010). Dla niezrównanego połączenia wiązką był HSS 12X8X3 /8 (β = 0.8) sugerowanie, że uplastycznienie czoła kolumny może być problemem. Dla połączenia dopasowanego wiązką był HSS 12X10X3 /8 (β = 1,0) umożliwiający przenoszenie obciążeń bezpośrednio na ściankę boczną. Wykorzystano protokół ładowania AISC do wstępnej kwalifikacji połączeń sejsmicznych (AISC 341-10) do załadowania połączeń. Zachowanie połączeń było zgodne z przewidywaniami z niezrównanym połączeniem pokazującym deformację na powierzchni kolumny, podczas gdy dopasowane połączenie było w stanie przenieść obciążenie na ściany boczne kolumny. Jednak oba połączenia nie powiodły się z powodu pęknięcia metalu nieszlachetnego kolumny w palcach rogu spoiny (Rysunek 3). Ta krucha awaria przy obrotach 0,4 rad. i 0,5 rad. potwierdzono odpowiednio, że połączenia bezpośrednio spawane nie zapewniają odpowiedniego zachowania w zastosowaniach sejsmicznych.

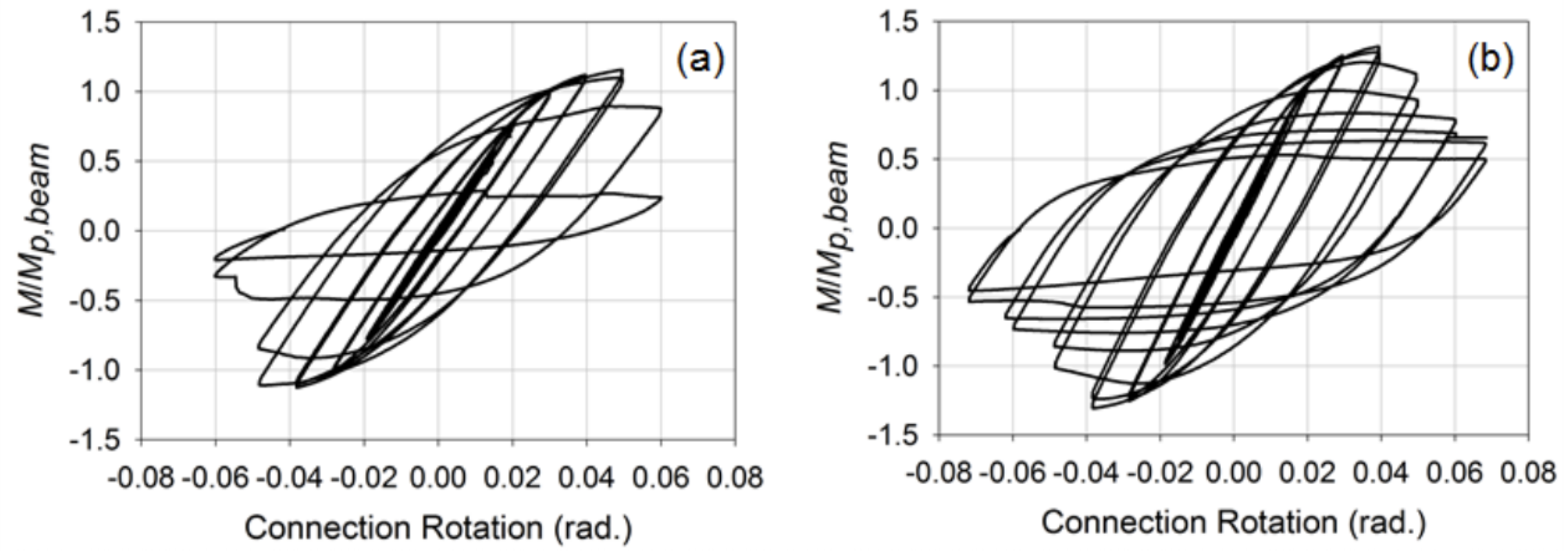
wzmocnione połączenia zostały następnie opracowane z uwzględnieniem płyt i zewnętrznych płyt membranowych, które są często stosowane w połączeniach słupów z szerokim kołnierzem w celu zapewnienia lepszego mechanizmu przenoszenia sił naprężenia i ściskania na ściankę boczną kolumny i zminimalizowania stężeń naprężeń umieszczonych na ścianie bocznej kolumny.spoiny. Dla tych połączeń wiązki były prętami HSS 12x8x3/8 (β = 0,8). Informacje dotyczące konkretnej procedury stosowanej do projektowania i wyszczególniania tych połączeń można znaleźć w Fadden And McCormick (2014b)i Fadden et al. (2015). Umieszczone pod tym samym obciążeniem, co połączenia niezabezpieczone, połączenia wykazały bardziej stabilne zachowanie z zawiasem z tworzywa sztucznego występującym z dala od powierzchni czołowej kolumny na końcu przelotowej lub zewnętrznej płyty membrany (ryc. 4). Oba połączenia również były w stanie osiągnąć 0,4 rad. rotacji przed poddaniem się miejscowemu wyboczeniu, które spowodowało degradację pojemności momentu. Jednak złamanie rozpoczęło się w rogu wiązki HSS z powodu cykli przy dużych obrotach 0,7 rad. Porównanie znormalizowanych krzywych momentu obrotowego dla dopasowanych i zewnętrznych połączeń płyt membranowych można zobaczyć na fig. 5. Ogólnie rzecz biorąc, wzmocnione połączenia wykazały obiecujące zastosowanie sejsmicznych systemów ramek momentowych Hss-Do-HSS, ale potrzeba więcej pracy, aby przenieść te połączenia w kierunku ewentualnej kwalifikacji wstępnej.

AISC. (2010). „Seismic Provisions for Structural Steel Buildings”. ANSI/AISC 341-10. American Institute of Steel Construction, Chicago, IL.

(2010). „Specifications for Structural Steel Buildings”. ANSI/AISC 360-10 American Institute of Steel Construction, Chicago, IL.

AWS. (2010). „Strukturalny Kod Spawalniczy”. ANSI / AWS D1. 1, American Welding Society, Miami, FL.

Fadden, F. I McCormick, J. (2014a). „Finite Element Model of the Cyclic Bending Behavior of Hollow Structural Sections”. Journal of Constructional Steel Research, 94, 64-75.

Fadden, F. And McCormick, J. (2014b). HSS-to-HSS Seismic Moment Connection Performance and Design (ang.). Journal of Constructional Steel Research, 101, 373-384.

Fadden, F., Wei, D., And McCormick, J. (2015). „Cyclic Testing of Welded HSS-to-HSS Moment Connections for Seismic Applications”. ASCE Journal of Structural Engineering, 141 (2), 04014109-1-14.

Jubb, J. E. M. and Redwood, R. G. (1966). „Design of Joints to Box Sections”. The Institution of Structural Engineers, Conference on Industrialized Building and the Structural Engineer, Institute of Structural Engineers, Londyn.

Korol, R. M., El-Zanaty, M., and Brady, F. J. (1977). „Nierówna Szerokość połączeń kwadratowych kształtowników pustych w kratownicach Vierendeel”. Canadian Journal of Civil Engineering, 4, 190-201.

Packer, J. A. (1993). „Połączenia chwilowe między prostokątnymi sekcjami wydrążonymi”. Journal of Constructional Steel Research, 25, 63-81.

Packer, J. A., Wardenier, J., Zhao, X.-L., van der Vegte, G. J. and Kurobane, Y. (2010). Design Guide 3: for Rectangular Hollow Section (RHS) Joints under Predominantly Static Loading 2nd Edition. CIDECT, Kanada.

Wardenier, J. (1982). Hollow Section Joints (Ang.). Delft University Press, Delft, Holandia.

wrzesień 2016

Pobierz PDF