oceniając Kappa Cohena

wartość kappa może być mniejsza niż 0 (ujemna). Wynik 0 oznacza, że istnieje losowa umowa między oceniającymi, podczas gdy wynik 1 oznacza, że istnieje pełna zgoda między oceniającymi. W związku z tym wynik mniejszy niż 0 oznacza, że jest mniej porozumienia niż przypadkowa szansa. Poniżej pokażę Ci formułę, aby to wypracować, ale ważne jest, abyś zapoznał się z rysunkiem 4, aby mieć silne zrozumienie.

powód, dla którego podświetlałem dwie siatki, stanie się jasny Za chwilę, ale na razie pozwólcie, że podzielę każdą siatkę.

a => całkowita liczba wystąpień, które obie oceny stwierdziły, że były poprawne. Raterzy się zgadzają.

B => całkowita liczba instancji, które rater 2 powiedział, że były nieprawidłowe, ale Rater 1 powiedział, że były poprawne. To nieporozumienie.

C => całkowita liczba instancji, które rater 1 powiedział, że były nieprawidłowe, ale Rater 2 powiedział, że były poprawne. Jest to również niezgoda.

D => całkowita liczba wystąpień, które oba Ratery stwierdziły, że były nieprawidłowe. Raterzy się zgadzają.

aby obliczyć wartość kappa, musimy najpierw poznać prawdopodobieństwo porozumienia (to wyjaśnia, dlaczego zaznaczyłem przekątną porozumienia). Wzór ten otrzymuje się przez dodanie liczby testów, w których liczniki się zgadzają, a następnie podzielenie go przez całkowitą liczbę testów. Na przykładzie z rysunku 4 oznaczałoby to (A + D)/(A + B+ C+ D).

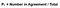
idealne! Następnym krokiem jest obliczenie prawdopodobieństwa losowej umowy. Korzystając z rysunku 4 jako wskazówki, wartością oczekiwaną jest całkowita liczba razy, które Rater 1 powiedział poprawnie, podzielona przez całkowitą liczbę instancji, pomnożona przez całkowitą liczbę razy, które Rater 2 powiedział poprawnie, podzielona przez całkowitą liczbę instancji, dodana do całkowitej liczby razy, które Rater 1 powiedział nieprawidłowo, pomnożona przez całkowitą liczbę razy, które Rater 2 powiedział nieprawidłowo. Jest to dużo informacji do wzięcia, więc na rysunku 6 sformułowałem to równanie za pomocą powyższej siatki.

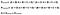
Lastly, the formula for Cohen’s Kappa is the probability of agreement take away the probability of random agreement divided by 1 minus the probability of random agreement.

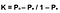
Super! Jesteś teraz w stanie odróżnić wiarygodność od trafności, wyjaśnić kappa Cohena i ocenić go. Ta statystyka jest bardzo przydatna, chociaż ponieważ zrozumiałem, jak to działa, teraz wierzę, że może być niedostatecznie wykorzystana podczas optymalizacji algorytmów do określonego metryki. Co więcej, kappa Cohena wykonuje również dobrą pracę, mierząc zarówno wielopoziomowe, jak i niezrównoważone problemy klasowe.

P. S. Jeśli jest coś, co chcesz, żebym omówił z nauką o danych, możesz wysłać do mnie wiadomość na Twitterze @KurtisPykes lub zostawić odpowiedź na ten post.