Interquartile Ranges & Outliers
Quartiles & Boxes5-Number SummaryIQRs & wartości odstające
purplemath
„zakres międzykwartylowy”, w skrócie „IQR”, jest po prostu szerokością pola na wykresie box-and-Whisker. Oznacza to, że IQR = Q3 – Q1 . IQR może być używany jako miara rozmieszczenia wartości.
Statystyka zakłada, że twoje wartości są zgrupowane wokół jakiejś wartości centralnej. IQR informuje, jak rozłożone są” środkowe „wartości; może być również użyty do określenia, kiedy niektóre inne wartości są „za daleko” od wartości centralnej. Te „zbyt odległe” punkty nazywane są” odstającymi”, ponieważ” leżą poza ” zakresem, w którym ich oczekujemy.
IQR to długość Pudełka na wykresie pudełka i wąsa. Wartość odstająca to każda wartość, która leży więcej niż półtora raza długości pudełka z obu końców pudełka.
treść znajduje się poniżej
MathHelp.com
oznacza to, że jeśli punkt danych znajduje się poniżej Q1 – 1,5×IQR lub powyżej Q3 + 1,5×IQR, jest on postrzegany jako zbyt odległy od centralnych wartości, aby był rozsądny. Może uderzyłeś w wagę, kiedy dokonywałeś tego jednego pomiaru, a może twój partner z laboratorium jest idiotą i nigdy nie powinieneś pozwolić mu dotykać żadnego sprzętu. Kto wie? Ale bez względu na ich przyczynę, odstające są te punkty, które nie wydają się”pasować”.
Dlaczego półtorej szerokości skrzynki dla odstających? Dlaczego ta konkretna wartość demarkuje różnicę między wartościami” akceptowalnymi” i „niedopuszczalnymi”? Ponieważ, kiedy John Tukey wynalazł Wykres box-and-whisker w 1977, aby wyświetlić te wartości, wybrał 1,5×IQR jako linię demarkacji dla wartości odstających. To działa dobrze, więc nadal korzystamy z tej wartości od tego czasu. Jeśli przejdziesz dalej do statystyk, przekonasz się, że ta miara racjonalności, dla danych o kształcie krzywej Dzwonkowej, oznacza, że zwykle tylko może nawet jeden procent danych będzie zawsze wartości odstające.
możesz użyć widżetu matematycznego poniżej, aby poćwiczyć znajdowanie zakresu Międzykwartylowego, zwanego również „H-spread” (lub pominąć widżet i kontynuować lekcję). Wypróbuj wprowadzone ćwiczenie lub wpisz własne ćwiczenie. Następnie kliknij przycisk i przewiń w dół do „Znajdź zakres Międzykwartylowy (H-Spread)”, aby porównać swoją odpowiedź z odpowiedzią Mathwaya.
aby włączyć ten widget, zaakceptuj pliki cookie „preferencje”.
(kliknij „Dotknij, aby wyświetlić kroki”, które należy wykonać bezpośrednio na stronie Mathway, aby uzyskać płatną aktualizację.)
Po znalezieniu IQR możesz przejść do lokalizacji wartości odstających, jeśli takie istnieją.
-
Znajdź wartości odstające, jeśli występują, dla następującego zestawu danych:
10.2, 14.1, 14.4. 14.4, 14.4, 14.5, 14.5, 14.6, 14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
aby dowiedzieć się, czy są jakieś wartości odstające, najpierw muszę znaleźć IQR. Istnieje piętnaście punktów danych, więc mediana będzie na ósmej pozycji:
(15 + 1) ÷ 2 = 8
następnie Q2 = 14,6.
po obu stronach mediany znajduje się siedem punktów danych. Dwie połówki to:
10, 2, 14, 1, 14, 4. 14, 4, 14, 4, 14, 5, 14, 5
…oraz:
14.7, 14.7, 14.7, 14.9, 15.1, 15.9, 16.4
Q1 jest czwartą wartością na liście, będącą środkową wartością pierwszej połowy listy; a Q3 jest dwunastą wartością, będącą środkową wartością drugiej połowy listy:
Q1 = 14.4
Q3 = 14.9
wtedy IQR jest podany przez:
IQR = 14.9 – 14.4 = 0.5
odstające będą dowolnymi punktami poniżej Q1 – 1.5 ×IQR = 14,4 – 0,75 = 13,65 lub więcej Q3 + 1,5×IQR = 14,9 + 0,75 = 15,65.
następnie wartości odstające są na poziomie:
10.2, 15.9 i 16.4
zawartość kontynuuje poniżej
wartości dla Q1 – 1.5×IQR i Q3 + 1.5×IQR to „ogrodzenia”, które zaznaczają” rozsądne ” wartości od wartości odstających. Odstające leżą poza ogrodzeniem.
Jeśli Twoje zadanie polega na rozważeniu nie tylko wartości odstających, ale także „wartości ekstremalnych”, to wartości dla Q1 – 1,5×IQR i Q3 + 1,5×IQR są „wewnętrznymi” ogrodzeniami, a wartości dla Q1 – 3×IQR i Q3 + 3×IQR są „zewnętrznymi” ogrodzeniami.
wartości odstające (oznaczone gwiazdkami lub otwartymi kropkami) znajdują się między wewnętrznym i zewnętrznym ogrodzeniem, a wartości skrajne (oznaczone dowolnym symbolem, którego nie użyłeś dla wartości odstających) znajdują się poza zewnętrznym ogrodzeniem.
przy okazji, Twoja książka może odnosić się do wartości „1.5×IQR” jako „krok”. Następnie wartości odstające będą liczbami, które są między jednym a dwoma krokami od zawiasów, a wartością ekstremalną będą liczby, które są więcej niż dwa kroki od zawiasów.
patrząc ponownie na poprzedni przykład, zewnętrzne ogrodzenia byłyby na poziomie 14,4 – 3×0,5 = 12,9 i 14,9 + 3×0,5 = 16,4. Ponieważ 16.4 znajduje się na górnym ogrodzeniu zewnętrznym, można by to uznać za wartość odstającą, a nie ekstremalną. Ale 10.2 jest całkowicie poniżej dolnego zewnętrznego ogrodzenia, więc 10.2 byłoby wartością ekstremalną.
Affiliate
Affiliate
Twój kalkulator graficzny może wskazywać, czy Wykres z wąsami zawiera wartości odstające. Na przykład powyższy problem obejmuje punkty 10.2, 15.9 i 16.4 jako odstające. Jedno ustawienie na moim kalkulatorze graficznym daje prosty wykres box-and-whisker, który wykorzystuje tylko podsumowanie pięciocyfrowe, więc najdalsze wartości odstające są pokazane jako punkty końcowe wąsów:

inne ustawienie kalkulatora daje wykres box-and-whisker ze specjalnie oznaczonymi wartościami odstającymi (w tym przypadku z symulacją otwartej kropki), a wąsy idą tylko tak daleko, jak najwyższe i najniższe wartości, które nie są wartościami odstającymi:

mój kalkulator nie rozróżnia wartości odstających od wartości ekstremalnych. Twoje też nie. Przed kolejnym testem sprawdź instrukcję obsługi.
Jeśli używasz kalkulatora graficznego, aby pomóc w tych wykresach, upewnij się, że wiesz, którego ustawienia powinieneś używać i co oznaczają wyniki, lub Kalkulator może dać ci idealnie poprawną, ale „złą” odpowiedź.
-
Znajdź wartości odstające i ekstremalne, jeśli istnieją, dla następującego zestawu danych i narysuj wykres box-and-whisker. Zaznacz wszystkie wartości odstające gwiazdką, a wartości ekstremalne otwartą kropką.
21, 23, 24, 25, 29, 33, 49
Reklama
aby znaleźć wartości odstające i ekstremalne, najpierw muszę znaleźć IQR. Ponieważ na liście znajduje się siedem wartości, mediana jest czwartą wartością, więc:
Q2 = 25
pierwsza połowa listy to:
21, 23, 24
…więc Q1 = 23; druga połowa to:
29, 33, 49
…więc Q3 = 33. Wtedy IQR jest podawany przez:
IQR = 33 – 23 = 10
wartości odstające będą dowolnymi wartościami poniżej:
23 – 1.5×10 = 23 – 15 = 8
…lub wyżej:
33 + 1.5×10 = 33 + 15 = 48
wartości ekstremalne będą następujące:
23 – 3×10 = 23 – 30 = -7
…lub wyżej:
33 + 3×10 = 33 + 30 = 63
więc mam outlier na 49 ale żadnych wartości ekstremalnych. Na mojej działce Nie będę miał najlepszego wąsa, ponieważ Q3 jest również najwyższym non-outlier. Więc moja działka wygląda tak:
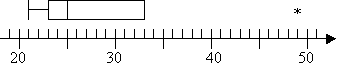
należy zauważyć, że metody, terminy i zasady opisane powyżej są tym, czego uczyłem i czego najczęściej uczyłem. Jednak kurs może mieć inne szczegółowe zasady lub Kalkulator może wykonywać obliczenia nieco inaczej. Być może będziesz musiał być nieco elastyczny w znalezieniu odpowiedzi specyficznych dla Twojego programu nauczania.
URL:https://www.purplemath.com/modules/boxwhisk3.htm
strona 1strona 2strona 3
Leave a Reply