Histogramy
wykresy słupkowe, rozkłady częstotliwości i histogramy
rozkłady częstotliwości, wykresy słupkowe i wykresy obwodowe
częstotliwość określonego zdarzenia jest liczbą czasów, w których zdarzenie występuje. Względna częstotliwość jestprzenośność obserwowanych odpowiedzi w kategorii.
przykład: zapytaliśmy uczniów, z jakiego kraju pochodzi ich samochód (lub bez samochodu) i sporządziliśmy zestawienie odpowiedzi. Następnie obliczyliśmy częstotliwość i względną częstotliwość każdej kategorii. Relatywna częstotliwość jest obliczana przez podzielenie częstotliwości przez całkowitą liczbę respondentów. The following tablesummarizes.
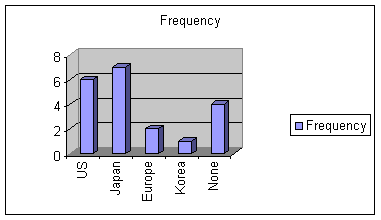
| Country | Frequency | Relative Frequency |
| US | 6 | 0.3 |
| Japan | 7 | 0.35 |
| Europe | 2 | 0.1 |
| Korea | 1 | 0.05 |
| None | 4 | 0.2 |
| Total | 20 | 1 |
Below is a bar graph for the car data. This bar graph is called a Paretochart since the height represents the frequency. Zauważ, że szerokości prętów są zawsze takie same.
często tworzymy Wykres kołowy nazywany wykresem kołowym tych danych, umieszczając go w okręgu o proporcjonalnej wielkości do częstotliwości.
Poniżej znajduje się Wykres koła, który pokazuje te dane.
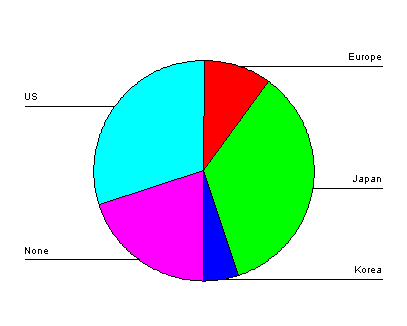
aby znaleźć kąty każdego z plastrów, używamy wzoru
na przykład do znalezienia kąta dla samochodów amerykańskich mamy
6
kąt = x 360 = 108 stopni
20
histogramy
histogramy są wykresami słupkowymi, których współrzędna pionowa jest liczbą częstotliwości i których współrzędna pozioma odpowiada interwałowi numerycznemu.
przykład:
głębokość jasności jeziora Tahoe została zmierzona w kilku różnych miejscach z wynikami w calach następująco:
15.4, 16.7, 16.9, 17.0, 20.2, 25.3, 28.8, 29.1, 30.4, 34.5,
36.7, 39.1, 39.4, 39.6, 39.8, 40.1, 42.3, 43.5, 45.6, 45.9,
48.3, 48.5, 48.7, 49.0, 49.1, 49.3, 49.5, 50.1, 50.2, 52.3
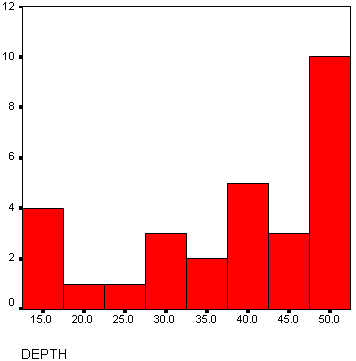
We use a frequency distribution table with class intervals of length 5.
| Class Interval | Frequency | Relative Frequency | Cumulative Relative Frequency |
| <20 | 4 | 0.129 | 0.129 |
| <25 | 1 | 0.032 | 0.161 |
| < 30 | 3 | 0.097 | 0.258 |
| < 35 | 2 | 0.065 | 0.323 |
| < 40 | 6 | 0.194 | 0.516 |
| < 45 | 3 | 0.097 | 0.613 |
| < 50 | 9 | 0.290 | 0.903 |
| < 55 | 3 | 0.097 | 1.000 |
| Total | 31 | 1.000 |
poniżej znajduje się Wykres histogramu
kształt histogramu
histogram jest unimodalny, jeśli jest jedenhump, bimodalny, jeśli są dwa garby i multimodalny, jeśli jest wiele garb. Histogram anonsymetryczny nazywa się przekrzywionym, jeśli nie jest symetryczny. Jeśli górny ogon jest dłuższy niż dolny ogon, jest dodatni. Jeśli górny ogon jest krótszy, niż jest ujemnyskowięty.
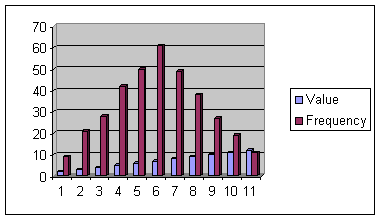Unimodal,Symmetric, Nonskewed
Nonsymmetric,Skewed Right
Bimodal
Leave a Reply