czy stary problem da nowy wgląd? Może elegancki dowód twierdzenia o czterech kolorach?
problem 4 kolorów jest jednym z najbardziej znanych problemów matematycznych. Opierał się dowodowi przez ponad sto lat, zanim ostatecznie uległ; w końcu istniał ważny dowód, ale taki, który polegał na ponad tysiącu godzin czasu komputerowego. Badania Jima Tilleya sugerują, że radykalne uproszczenie może być ostatecznie możliwe. Odkrył właściwość Kempe-locking, którą musi wykazać minimalny kontrprzykład do twierdzenia o czterech kolorach i sformułował przypuszczenie, oparte na rozległych badaniach, że diament Birkhoffa jest jedyną podstawową konfiguracją Kempe-locking.
kolorowanie grafu polega na przypisaniu etykiet lub kolorów do wierzchołków obiektu matematycznego znanego jako Graf. Problem 4-kolorowy stanowił jedną z pierwotnych motywacji do rozwoju algebraicznej teorii grafów. Kolorowanie Wykresów jest używane w wielu rzeczywistych problemach, takich jak minimalizacja konfliktów podczas planowania wydarzeń sportowych, planowania harmonogramów egzaminów i organizowania planów miejsc siedzących, nawet w przypadku umieszczenia kamery CCTV w budynku z wieloma narożnikami w celu Zminimalizowania nakładania się kamer. Stanowi również podstawę do łamigłówek Sudoku.
Problem 4 kolorów
Francis Guthrie, uczeń słynnego brytyjskiego matematyka i logika Augustusa De Morgana, postawił problem 4 kolorów w 1852 roku. Sformułował problem w odniesieniu do map, które spełniają określone warunki, takie jak nie zawierają żadnych dziur i mają Każdy region (np. kraj lub państwo) połączony tak, że żaden region nie istnieje w dwóch lub więcej nie przylegających częściach. Guthrie twierdził, że w przypadku takich map nigdy nie potrzeba więcej niż czterech kolorów, aby pokolorować mapę tak, aby żadne dwa sąsiednie regiony nie były tego samego koloru.
obecnie problem 4-kolorowy jest wyrażany w postaci wykresów, a zamiast kolorować regiony na mapach, jeden koloruje wierzchołki na wykresach. Wszystkie istniejące dowody twierdzenia o czterech kolorach pokazują, że minimalny kontrprzykład nie może istnieć. (Minimalnym kontrprzykładem jest najmniejszy Graf planarny, który wymaga więcej niż czterech kolorów do prawidłowego wybarwienia wierzchołków.) Należy wziąć pod uwagę tylko grafy planarne, które są triangulacjami, ponieważ każdy wykres, który nie jest triangulacją, można przekształcić w jeden, wstawiając krawędzie. Jeśli otrzymana triangulacja jest 4-kolorowa, to oryginalny wykres jest również 4-kolorowy. Bardzo przydatna jest możliwość ograniczenia kontroli do triangulacji.

wczesna próba udowodnienia
Alfred Bray Kempe, angielski prawnik i matematyk-amator, był osobą, której reputacja była najbardziej skażona jego nieudanym wysiłkiem. Swój sukces ogłosił w 1879 roku, a jego „dowód” został opublikowany w American Journal of Mathematics. Jedenaście lat później inny angielski matematyk, Percy Heawood, stworzył mapę, którą 4-kolorował aż do ostatniego regionu w taki sposób, że metoda Kempe ’ a nie powiodła się dla tego ostatniego regionu. Mimo porażki Kempe zostawił przydatne narzędzie-Łańcuch Kempe. Jest to maksymalny, połączony (każdy wierzchołek osiągalny z dowolnego innego ścieżką wzdłuż krawędzi) podgraf, w którym wszystkie wierzchołki używają dokładnie dwóch kolorów. Łańcuchy Kempe okazały się pomocne w barwieniu i ponownym barwieniu Wykresów. Patrz Rysunek 1.
byłoby zdumiewającym uproszczeniem
, gdyby sam diament Birkhoffa był kluczem do 4-kolorowości.
dowód w końcu
pierwszy ważny dowód został ogłoszony w 1976 roku przez Kennetha appela i Wolfganga Hakena. Wymagało to ponad tysiąca godzin czasu komputerowego, aby zweryfikować poszczególne aspekty ich argumentacji. To pojęcie polegania na kodzie komputerowym, potencjalnie zawierającym błędy wywołane przez człowieka (a ich kod zrobił!), a nie „ludzki” dowód, nie zadowolił dużej części społeczności matematycznej. Dowód appela i Hakena był elegancki w ogólnej strukturze, ale szczegóły były brzydkie.
dowód został udoskonalony w 1996 roku przez zespół czterech matematyków: Robertsona, Sandersa, Seymoura i Thomasa, ale nadal polegali na kodzie komputerowym, aby uzupełnić swój dowód. W 2010 roku Steinberger zaproponował kolejną odmianę. Jednak nadal nie ma całkowicie satysfakcjonującej odpowiedzi na pytanie, dlaczego twierdzenie o czterech kolorach jest prawdziwe. (Po udowodnieniu hipotezy uzyskał status twierdzenia.”)

i matematyk amator.
poszukiwanie alternatywnego dowodu
problem czterech kolorów jest tak łatwy do wyrażenia i zrozumienia, że wzbudził zainteresowanie wielu tysięcy matematyków-amatorów, wierzących, że mogą znaleźć prosty dowód klasyczny i tym samym stać się sławni. Ojciec Jima Tilleya, fizyk i dyrektor Royal Military College w Kanadzie w latach 1978-1984, był jednym z takich marzycieli. Za każdym razem, gdy czuł, że dokonał przełomu, prosił swojego syna, Jima, aby sprawdził jego pracę. Jim zawsze miał wadę. Mimo początkowego sceptycyzmu, że wysiłki ojca kiedykolwiek przyniosą owoce, zaraził się entuzjazmem do problemu czterech kolorów i zaczął intensywnie go badać.
Kempe-locking
badania Jima Tilleya doprowadziły do odkrycia nowej własności, którą musi wykazać minimalny kontrprzykład do twierdzenia o czterech kolorach. Nazwał go ” Kempe-locking.”Zdał sobie sprawę, że prawdopodobnie jest niezgodny z inną własnością, którą musi wykazać minimalny kontrprzykład-mianowicie., jak połączony jest wykres (ile wierzchołków należy usunąć z grafu, zanim się rozpadnie).
Kempe-locking Tilleya jest właściwością związaną z krawędzią w triangulacji. Pojęcie zaczyna się od usunięcia krawędzi xy między sąsiadującymi wierzchołkami X i y. Jeśli dla każdego 4-zabarwienia wykresu, w którym kolory X i y są takie same, nie ma sekwencji zamiany kolorów na łańcuchach Kempe ’ a, która powoduje, że kolor x różni się od koloru y, to mówi się, że pierwotna triangulacja jest zablokowana Kempe w odniesieniu do krawędzi xy. Tilley udowodnił, że minimalny kontrprzykład do twierdzenia o czterech kolorach musi być zablokowany Kempe w odniesieniu do każdej z jego krawędzi; każda krawędź w minimalnym kontrprzykładie musi mieć tę właściwość zabarwienia.
blokowanie Kempe jest szczególnie restrykcyjnym warunkiem, który staje się trudniejszy do spełnienia w miarę powiększania się triangulacji. Tilley postanowił odkryć, czy jest coś wspólnego z trójkątami, które mają krawędzie zamknięte Kempe. Jego najwcześniejsze poszukiwania Kempe-lockingu doprowadziły go do diamentu Birkhoffa.

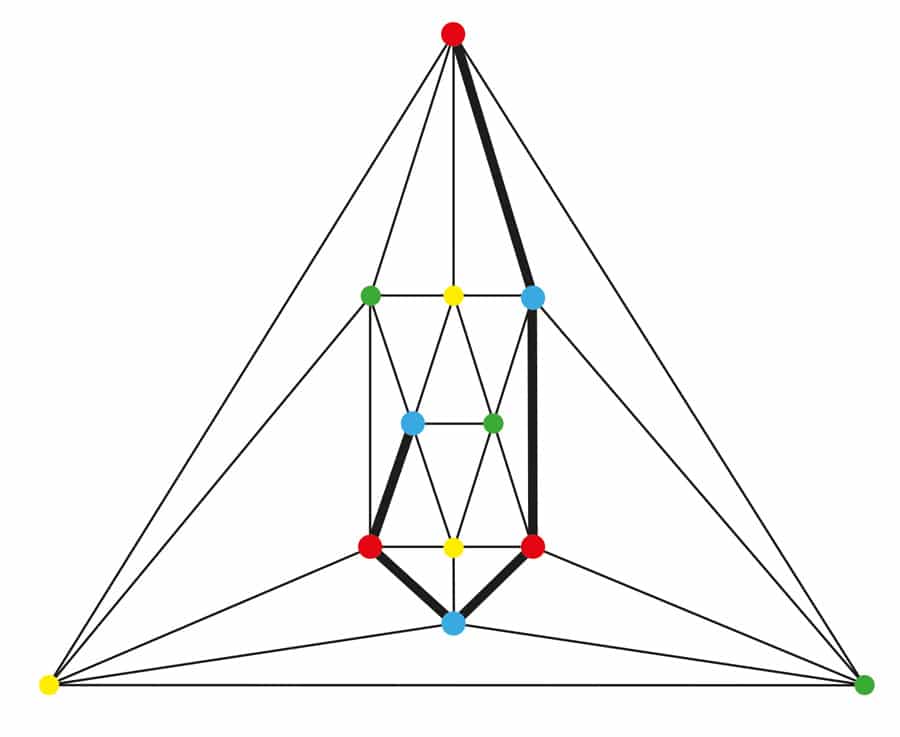
Rysunek 3. Dwa grafy planarne, jeden 4-połączony triangulacją na 6 wierzchołkach i jeden 5-połączony triangulacją na 17 wierzchołkach.
diament Birkhoffa
w 1913 roku G. D. Birkhoff odkrył, że pewna konfiguracja dziesięciu krajów na mapie (pierścień graniczny sześciu krajów, który otacza zestaw czterech krajów) ma ważną właściwość. Jeśli ta konfiguracja jest obecna na mapie i jeśli submapa z usuniętą konfiguracją jest 4-kolorowa, to cała mapa będzie 4-kolorowa. W związku z tym minimalny kontrprzykład nie może zawierać tej konkretnej konfiguracji. Stał się znany jako diament Birkhoffa. Tilley odkrył, że krawędź XY z blokadą Kempe wydaje się powstawać tylko wtedy, gdy x i y są również punktami końcowymi grafu diamentu Birkhoffa. Patrz Rysunek 2.
przypuszczenie jest łatwe do sformułowania, zrozumiałe i intrygujące, i oferuje przekonujące wyjaśnienie, dlaczego wszystkie grafy planarne są 4-kolorowe.
nie napotkawszy żadnej konfiguracji blokowania Kempe bez diamentu Birkhoffa, przypuszczał, że diament Birkhoffa jest jedyną „podstawową” konfiguracją blokowania Kempe, taką, która nie zawiera mniejszej konfiguracji blokowania Kempe jako subgrafu. Tilley stwierdził jednak, że nie może udowodnić swoich krytycznych przypuszczeń. To było frustrujące, ponieważ, jeśli to prawda, przypuszczenie bezpośrednio udowodniłoby twierdzenie o czterech kolorach. (Aby być minimalnym kontrprzykładem, triangulacja musiałaby zawierać subgraf diamentu Birkhoffa, ale gdyby tak było, nie mogłaby być minimalnym kontrprzykładem.)
przytłaczająca sprawa
zamiast udowadniać swoje przypuszczenia, Tilley zrobił kolejną najlepszą rzecz. Postanowił wcielić się w rolę eksperymentatora i zbudować przytłaczającą sprawę na poparcie swoich domysłów. Podzielił wszystkie istotne Trójkąty planarne na dwie klasy: te, w których co najmniej cztery wierzchołki muszą zostać usunięte przed rozpadnięciem się Wykresów (4-połączone) i te, w których co najmniej pięć wierzchołków musi zostać usuniętych przed rozpadnięciem się Wykresów (5-połączone). Patrz Rysunek 3. Pomocne w rozległych poszukiwaniach Tilleya było to, że musiał zbadać tylko jeden element każdej klasy izomorfizmu (wykresy, które są strukturalnie identyczne). Tilley zbadał wszystkie 8044 klasy izomorfizmu 4-połączonych trójkątów planarnych na maksymalnie 15 wierzchołkach i wszystkie 9733 klasy izomorfizmu 5-połączonych trójkątów planarnych na maksymalnie 24 wierzchołkach. Znalazł tylko trzy trójkąty zamknięte Kempe. Każda odkryta krawędź Kempe-locked zawierała diament Birkhoff ’ a i każda występowała w 4 połączonych ze sobą triangulacji. Nie było żadnego z 5 połączonych trójkątów.

Tilley rozszerzył swoje poszukiwania wśród 4 połączonych trójkątów, badając wszystkie 30 926 klas izomorfizmu na 16 wierzchołkach i wszystkie 158 428 klas izomorfizmu na 17 wierzchołkach. Ograniczenia czasowe oznaczały ograniczenie jego poszukiwań do próbek 100 000 losowo generowanych nieizomorficznych trójkątów, każdy dla klas na 18,19 i 20 wierzchołkach. Rozszerzone Wyszukiwanie wykazało 45 dodatkowych triangulacji zablokowanych Kempe, ale dokładnie takie same wyniki jak oryginalne wyszukiwanie: każda krawędź zablokowana Kempe w triangulacji zawierała powiązany diament Birkhoffa.
skąd stąd?
rozległe poszukiwania Tilleya łatwo potwierdziły, że diament Birkhoffa jest podstawową konfiguracją blokującą Kempe. Dokładnie przetestował swoje domysły, ale nie zostały udowodnione. Jeśli (lub kiedy) hipoteza Tilleya okaże się prawdziwa, tzn. że sam diament Birkhoffa jest kluczem do 4-kolorowości, byłoby to zdumiewające uproszczenie problemu: pojedyncza konfiguracja, która wszystko wyjaśnia – matematyczna elegancja.

udowodnienie 4-kolorowej hipotezy wymagało wysiłku wielu wybitnych matematyków. Przypuszczenie tilleya, że diament Birkhoffa jest jedyną podstawową konfiguracją blokującą Kempe, może być jeszcze trudniejsze do udowodnienia. Jednak dowody eksperymentalne są mocne. Teoretycy mogą powiedzieć ” po co się trudzić? Odpowiedź tilleya jest taka, że nienasycona ciekawość zwycięży: „w końcu przypuszczenie jest łatwe do sformułowania, zrozumiałe i intrygujące, i oferuje przekonujące wyjaśnienie, dlaczego wszystkie grafy planarne są 4-kolorowe.”
odpowiedź osobista
co początkowo wzbudziło twój entuzjazm dla problemu 4 kolorów i skłoniło cię do tak intensywnego studiowania go?
To była obsesja mojego ojca na punkcie problemu na emeryturze i jego chęć wykorzystania mnie jako forum dla swoich pomysłów.
Jakie są Twoje plany na przyszłe badania w tej dziedzinie?
niedawno recenzowałem skomplikowaną pracę, w której omówiono zupełnie inne podejście do problemu 4-kolorowego. W obecnej formie Papier ma wady. Ale ma obietnicę. Może pokuszę się o współpracę.
Leave a Reply