Ciąg Fibonacciego
ciąg Fibonacciego jest ciągiem liczb:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
następna liczba znajduje się przez dodanie dwóch liczb przed nią:
- 2 znajduje się przez dodanie dwóch liczb przed nią (1+1),
- 3 znajduje się przez dodanie dwóch liczb przed nią (1+2),
- 5 to (2+3),
- i tak dalej!
przykład: następna liczba w powyższej sekwencji to 21+34 = 55
to takie proste!
oto dłuższa lista:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
możesz wymyślić kolejne liczby?
tworzy spiralę
kiedy robimy kwadraty o tych szerokościach, otrzymujemy ładną spiralę:
Czy widzisz, jak kwadraty pasują do siebie?
na przykład 5 i 8 tworzą 13, 8 i 13 tworzą 21 itd.

ta spirala występuje w naturze!
Zobacz: Natura, złoty podział i Fibonacciego
reguła
ciąg Fibonacciego może być zapisany jako „reguła” (zobacz sekwencje i szeregi).
Po pierwsze, wyrazy są numerowane od 0 i dalej w ten sposób:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
tak więc wyrażenie numer 6 nazywa się x6 (co jest równe 8).
|
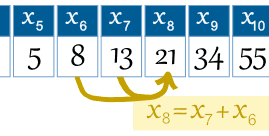
przykład: 8. kadencja to x8 = x7 + x6 |
 |
więc możemy napisać regułę:
reguła to xn = xn−1 + xn−2
gdzie:
- xn jest wyrażeniem liczby „n”
- xn−1 jest wyrażeniem poprzedzającym (n−1)
- xn−2 jest wyrażeniem poprzedzającym (n−2)
przykład: wyrażenie 9 jest obliczane w następujący sposób:
złoty współczynnik
a tu niespodzianka. Kiedy weźmiemy dowolne dwie kolejne liczby Fibonacciego (jedna po drugiej), ich stosunek jest bardzo zbliżony do Złotego współczynnika „φ”, który wynosi w przybliżeniu 1,618034…
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |
nie musimy zaczynać od 2 i 3, tutaj losowo wybrałem 192 i 16 (i dostałem sekwencję 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, …):
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
192
|
16
|
0.08333333… | |
|
16
|
208
|
13 | |
|
208
|
224
|
1.07692308… | |
|
224
|
432
|
1.92857143… | |
|
…
|
…
|
… | |
|
7408
|
11984
|
1.61771058… | |
|
11984
|
19392
|
1.61815754… | |
|
…
|
…
|
… |
uzyskanie dobrych wartości zajmuje więcej czasu, ale pokazuje, że nie tylko Sekwencja Fibonacciego może to zrobić!
używając Złotego współczynnika do obliczania liczb Fibonacciego
i jeszcze bardziej zaskakujące jest to, że możemy obliczyć dowolną liczbę Fibonacciego używając Złotego współczynnika:
xn = φn − (1−φ)n√5
odpowiedź wychodzi jako liczba całkowita, dokładnie równa dodaniu dwóch poprzednich wyrazów.
przykład: x6
x6 = (1.618034…)6 − (1−1.618034…) 6√5
kiedy użyłem na tym kalkulatora (wpisując tylko złoty stosunek do 6 miejsc po przecinku) otrzymałem odpowiedź 8.00000033 , dokładniejsze obliczenia byłyby bliższe 8.
spróbuj n=12 i zobacz co dostaniesz.
Możesz również obliczyć liczbę Fibonacciego, mnożąc poprzednią liczbę Fibonacciego przez Złoty Współczynnik, a następnie zaokrąglając (działa dla liczb powyżej 1):
przykład: 8 × φ = 8 × 1.618034… = 12.94427… = 13 (zaokrąglone)
kilka ciekawych rzeczy
oto znowu ciąg Fibonacciego:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | … |
istnieje ciekawy wzór:
- spójrz na liczbę x3 = 2. Każda trzecia liczba jest wielokrotnością 2 (2, 8, 34, 144, 610, …)
- spójrz na liczbę x4 = 3. Każda czwarta liczba jest wielokrotnością 3 (3, 21, 144,…)
- spójrz na liczbę x5 = 5. Każda piąta liczba jest wielokrotnością 5 (5, 55, 610,…)
i tak dalej (każda N-ta liczba jest wielokrotnością xn).
1/89 = 0.011235955056179775…
zauważ, że kilka pierwszych cyfr (0,1,1,2,3,5) to ciąg Fibonacciego?
w pewnym sensie wszystkie one są, z wyjątkiem liczb wielocyfrowych (13, 21 itp.) nakładają się na siebie, jak to:
… itd …
0.011235955056179775… =1/89
terminy poniżej zera
Sekwencja działa również poniżej zera, w następujący sposób:
| n= | … | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| xn = | … | −8 | 5 | −3 | 2 | −1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | … |
(udowodnij sobie, że każda liczba jest znaleziona, dodając dwie liczby przed nią!)
w rzeczywistości Sekwencja poniżej zera ma takie same liczby jak Sekwencja powyżej zera, z tym że podążają za +-+- … wzór. Można to zapisać w następujący sposób:
x−n = (-1)n+1 xn
, który mówi, że wyrażenie „−n” jest równe (-1)N+1 razy wyrażenie „n”, A wartość (-1) N+1 porządnie czyni poprawną +1, -1, +1, -1, … wzór.
Historia
Fibonacci nie był pierwszym, który dowiedział się o sekwencji, była ona znana w Indiach setki lat wcześniej!

o Fibonaccim Mężczyzną
był Leonardo Pisano Bogollo i żył między 1170 a 1250 rokiem we Włoszech.
„Fibonacci” był jego przezwiskiem, co z grubsza oznacza „syn Bonacciego”.
oprócz tego, że jest znany z ciągu Fibonacciego, pomógł rozpowszechnić liczby Hinduistyczno-Arabskie (jak nasze obecne liczby 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) przez Europę w miejsce cyfr rzymskich (I, II, III, IV, V itd.). To oszczędziło nam wielu kłopotów! Dziękuję Leonardo.

dzień Fibonacciego
dzień Fibonacciego jest 23 listopada, ponieważ ma cyfry „1, 1, 2, 3”, które są częścią sekwencji. Więc następny listopad 23 niech wszyscy wiedzą!


Leave a Reply