Całki określone
warto najpierw przeczytać wprowadzenie do integracji!
Integracja
|
integracja może być używana do wyszukiwania obszarów, woluminów, punktów centralnych i wielu przydatnych rzeczy. Ale często jest używany do znajdowania obszaru pod wykresem funkcji takiej jak ta: |
 |
|
|
obszar można znaleźć, dodając plasterki, które zbliżają się do zera w szerokości: i istnieją reguły integracji, które pomagają nam uzyskać odpowiedź. |
 |
notacja
symbolem „całki” jest stylowe „s” (dla „sumy”, idea sumowania plasterków):
Po symbolu całki umieszczamy funkcję, której chcemy znaleźć całkę (zwaną całką).
a następnie zakończ dx, aby znacząc, że plasterki idą w kierunku x (i zbliżają się do zera na szerokość).
Całka określona
Całka określona ma wartość początkową i końcową: innymi słowy jest przedział .
a i b (zwane limitami, ograniczeniami lub granicami) są umieszczane na dole i na górze „S”, W ten sposób:
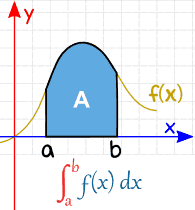 |
 |
|
| Definite Integral (from a to b) |
Indefinite Integral (no specific values) |
We find the Definite Integral by calculating the Indefinite Integral at a, and at b, then subtracting:
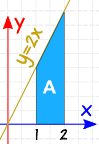
przykład: co to jest 2 ∫ 1 2x dx
jesteśmy proszeni o całkę określoną, od 1 do 2, Z 2x dx
najpierw musimy znaleźć nieokreślony integral.
korzystając z reguł integracji znajdujemy, że ∫2x dx = x2 + C
teraz Oblicz to przy 1 i 2:
- Przy x=1: ∫2x dx = 12 + C
- przy x=2: ∫2x dx = 22 + c
Odejmij:
i „C” zostaje anulowane … zatem z Całkami określonymi możemy ignorować C.
wynik:

Sprawdź: przy tak prostym kształcie spróbujmy również obliczyć powierzchnię według geometrii:
a = 2+42 × 1 = 3
tak, ma powierzchnię 3.
(Yay!)
notacja: Możemy pokazać całkę nieokreśloną (bez +C) wewnątrz nawiasów kwadratowych, z ograniczeniami a i b Po, jak to:
przykład (ciąg dalszy)
dobry sposób na pokazanie odpowiedzi:
x DX
=
spróbujmy innego przykładu:
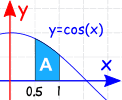
Example:
The Definite Integral, from 0.5 to 1.0, of cos(x) dx:
(Note: x must be in radians)
The Indefinite Integral is: ∫cos(x) dx = sin(x) + C
We can ignore C for definite integrals (as we saw above) and we get:
=
And another example to make an important point:
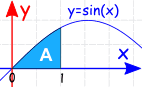
Example:
The Definite Integral, from 0 to 1, of sin(x) dx:
Całka nieokreślona to: ∫sin(x) dx = −cos(x) + c
skoro idziemy od 0, Czy możemy po prostu obliczyć całkę w x=1?
−cos(1) = -0.540…
Co? Jest negatywny? Ale na wykresie wygląda to pozytywnie.
Cóż … popełniliśmy błąd!
ponieważ musimy odjąć całkę W x=0. Nie powinniśmy zakładać, że jest to zero.
zróbmy to właściwie, odejmując jedno od drugiego:
=
1
tak jest lepiej!
ale możemy mieć obszary ujemne, gdy krzywa znajduje się poniżej osi:

przykład:
Całka określona, od 1 do 3, cos(x) DX:
zauważ, że część jest pozytywna, a część negatywna.
Całka określona wyliczy wartość netto.
zróbmy obliczenia:
=
w skoku jest więcej ujemnych niż dodatnich, z wynikiem netto -0,700….
dlatego musimy pamiętać o tej ważnej rzeczy:
spróbuj zintegrować cos(x) z różnymi wartościami początkowymi i końcowymi, aby zobaczyć na własne oczy, jak działają pozytywy i negatywy.
obszar dodatni
ale czasami chcemy, aby cały obszar był traktowany jako dodatni (bez odejmowania części poniżej osi).
w takim przypadku musimy obliczyć obszary osobno, jak w tym przykładzie:

przykład: Jaki jest całkowity obszar pomiędzy y = cos (x) i osią x, OD x = 1 do x = 3?
To jest jak przykład, który właśnie zrobiliśmy, ale teraz oczekujemy, że cały obszar jest pozytywny (wyobraźmy sobie, że musieliśmy go pomalować).
więc teraz musimy zrobić części osobno:
- jeden dla obszaru powyżej osi x
- jeden dla obszaru poniżej osi x
krzywa przecina oś x W x = π/2, więc mamy:
od 1 do π/2:
= sin(π/2)-Sin(1)
C = grzech(3) − grzech(π/2)
ostatni wynik jest ujemny, ale chcemy, aby był dodatni, więc:
całkowita powierzchnia = 0,159… + 0,859… = 1,018…
to bardzo różni się od odpowiedzi w poprzednim przykładzie.
ciągły
o tak, funkcja, którą całkujemy, musi być ciągła między a i b: brak otworów, skoków lub pionowych asymptot (gdzie funkcja kieruje się w górę / w dół w kierunku nieskończoności).
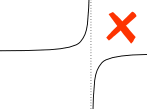
przykład:
asymptota pionowa między a i b wpływa na całkę określoną.
właściwości
Area above − area below
Całka dodaje obszar nad osią, ale odejmuje obszar poniżej, dla „wartości netto”:
Dodawanie funkcji
Całka F+g równa się Całka F plus całka g:
aby anulować przedziału
i
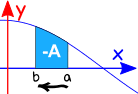
zmieniając kierunek interwał daje negatyw od pierwotnego kierunku.
![]()

Leave a Reply