Analiza regresji liniowej w Excelu
samouczek wyjaśnia podstawy analizy regresji i pokazuje kilka różnych sposobów wykonywania regresji liniowej w Excelu.
wyobraź sobie to: otrzymujesz mnóstwo różnych danych i jesteś proszony o przewidzenie przyszłorocznych wyników sprzedaży dla Twojej firmy. Odkryłeś dziesiątki, a może nawet setki czynników, które mogą mieć wpływ na liczby. Ale skąd wiesz, które z nich są naprawdę ważne? Uruchom analizę regresji w Excelu. Da ci odpowiedź na to i wiele innych pytań: Jakie czynniki mają znaczenie, a które można zignorować? Jak ściśle te czynniki są ze sobą powiązane? A na ile możesz być pewien przewidywań?
- Analiza regresji w Excelu
- regresja liniowa w Excelu za pomocą narzędzia Analitycznegopak
- narysuj wykres regresji liniowej
- Analiza regresji w Excelu za pomocą formuł
Analiza regresji w Excelu-podstawy
w modelowaniu statystycznym Analiza regresji służy do oszacowania zależności między dwiema lub więcej zmiennymi:
zmienna zależna (aka zmienna kryterium) jest głównym czynnikiem, który próbujesz zrozumieć i przewidzieć.
zmienne niezależne (zwane także zmiennymi objaśniającymi lub predyktorami) to czynniki, które mogą wpływać na zmienną zależną.
Analiza regresji pomaga zrozumieć, jak zmienna zależna zmienia się, gdy jedna ze zmiennych niezależnych się zmienia i pozwala matematycznie określić, która z tych zmiennych naprawdę ma wpływ.
technicznie model analizy regresji opiera się na sumie kwadratów, co jest matematycznym sposobem znajdowania rozproszenia punktów danych. Celem modelu jest uzyskanie jak najmniejszej sumy kwadratów i narysowanie linii, która jest najbliższa danym.
w statystykach rozróżniają regresję prostą i wielokrotną liniową. Prosta regresja liniowa modeluje zależność między zmienną zależną a jedną zmienną niezależną za pomocą funkcji liniowej. Jeśli używasz dwóch lub więcej zmiennych objaśniających do przewidywania zmiennej zależnej, masz do czynienia z wielokrotną regresją liniową. Jeśli zmienna zależna jest modelowana jako funkcja nieliniowa, ponieważ relacje danych nie podążają za linią prostą, zamiast tego użyj regresji nieliniowej. W tym samouczku skupimy się na prostej regresji liniowej.
jako przykład przyjrzyjmy się liczbom sprzedaży parasoli za ostatnie 24 miesiące i dowiedzmy się, jakie są średnie miesięczne opady deszczu w tym samym okresie. Narysuj tę informację na wykresie, a linia regresji pokaże zależność między zmienną niezależną (opad) i zmienną zależną (sprzedaż parasolowa):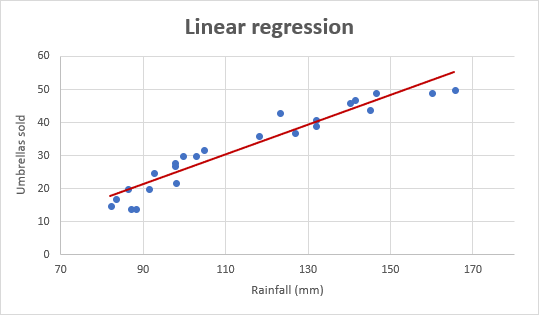
równanie regresji liniowej
matematycznie regresja liniowa jest zdefiniowana przez to równanie:
gdzie:
- X jest zmienną niezależną.
- y jest zmienną zależną.
- a to punkt przecięcia osi Y, który jest oczekiwaną średnią wartości y, gdy wszystkie zmienne x są równe 0. Na wykresie regresji jest to punkt, w którym linia przecina oś Y.
- b jest nachyleniem linii regresji, która jest szybkością zmian dla y jako zmian X.
- ε jest terminem błędu losowego, który jest różnicą między rzeczywistą wartością zmiennej zależnej a jej przewidywaną wartością.
równanie regresji liniowej zawsze ma termin błędu, ponieważ w rzeczywistości predyktory nigdy nie są idealnie precyzyjne. Jednak niektóre programy, w tym Excel, wykonują obliczenia terminów błędów za kulisami. Tak więc w programie Excel wykonujesz regresję liniową za pomocą metody najmniejszych kwadratów i szukasz współczynników a i b takich, że:
na naszym przykładzie równanie regresji liniowej przybiera następujący kształt:
Umbrellas sold = b * rainfall + a
istnieje kilka różnych sposobów znalezienia a i b. trzy główne metody przeprowadzania analizy regresji liniowej w programie Excel to:
- narzędzie regresji dołączone do Narzędzia Analitycznegopak
- Wykres punktowy z linią trendu
- wzór regresji liniowej
poniżej znajdziesz szczegółowe instrukcje dotyczące korzystania z każdej metody.
jak wykonać regresję liniową w Excelu za pomocą Analysis ToolPak
Ten przykład pokazuje, jak uruchomić regresję w Excelu za pomocą specjalnego narzędzia dołączonego do dodatku Analysis ToolPak.
Włącz dodatek Analysis ToolPak
narzędzie Analysis ToolPak jest dostępne we wszystkich wersjach programu Excel 2019 do 2003, ale nie jest domyślnie włączone. Musisz go włączyć ręcznie. Oto jak:
- w swoim Excelu kliknij plik>.
- w oknie dialogowym Opcje programu Excel wybierz dodatki na lewym pasku bocznym, upewnij się, że Dodatki programu Excel są zaznaczone w Zarządzaj i kliknij idź.
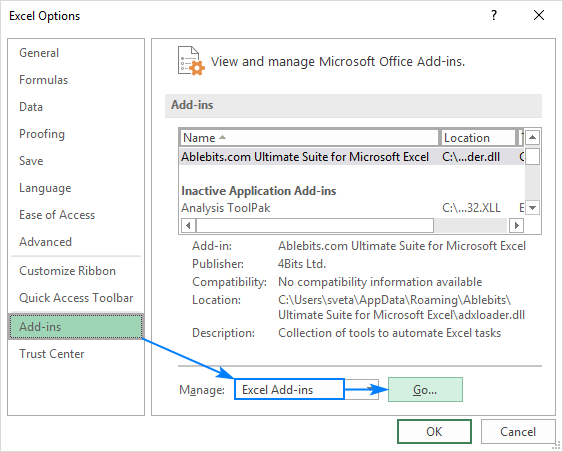
- w oknie dialogowym Dodawanie zaznacz opcję Analysis Toolpak i kliknij OK:
spowoduje to dodanie narzędzi do analizy danych do karty danych wstążki programu Excel.
Uruchom analizę regresji
w tym przykładzie wykonamy prostą regresję liniową w programie Excel. Mamy listę średnich miesięcznych opadów z ostatnich 24 miesięcy w kolumnie B, która jest naszą zmienną niezależną (predictor), oraz liczbę sprzedanych parasoli w kolumnie C, która jest zmienną zależną. Oczywiście istnieje wiele innych czynników, które mogą mieć wpływ na sprzedaż, ale na razie skupiamy się tylko na tych dwóch zmiennych: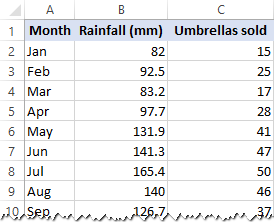
Po włączeniu funkcji Analysis Toolpak wykonaj następujące kroki, aby wykonać analizę regresji w programie Excel:
- na karcie Dane w grupie analizy kliknij przycisk Analiza danych.
- Wybierz regresję i kliknij OK.
- w oknie dialogowym regresji skonfiguruj następujące ustawienia:
- Wybierz wejściowy Zakres Y, który jest zmienną zależną. W naszym przypadku jest to sprzedaż parasolowa (C1: C25).
- Wybierz wejściowy Zakres X, czyli Twoją niezależną zmienną. W tym przykładzie jest to średnia miesięczna suma opadów (B1: B25).
jeśli budujesz model regresji wielokrotnej, wybierz dwie lub więcej sąsiadujących kolumn z różnymi niezależnymi zmiennymi.
- zaznacz pole etykiety, jeśli na górze zakresów X i Y znajdują się nagłówki.
- wybierz preferowaną opcję wyjścia, nowy arkusz roboczy w naszym przypadku.
- Opcjonalnie zaznacz pole wyboru pozostałości, aby uzyskać różnicę między przewidywanymi i rzeczywistymi wartościami.
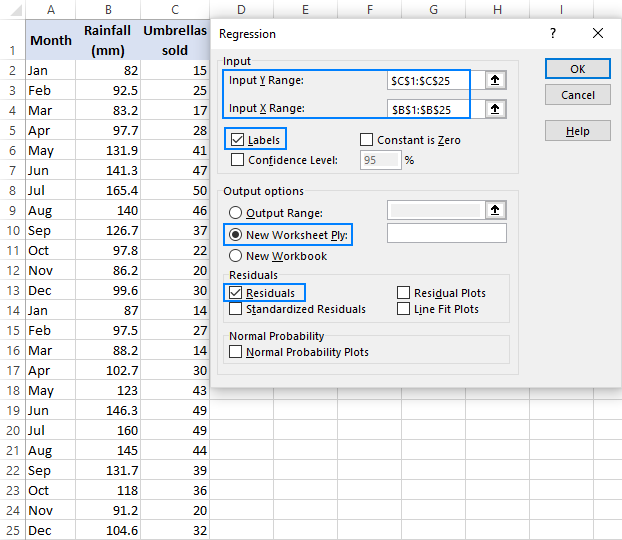
- kliknij OK i obserwuj wynik analizy regresji utworzony przez Excel.
interpretacja wyników analizy regresji
jak przed chwilą widziałeś, uruchamianie regresji w programie Excel jest łatwe, ponieważ wszystkie obliczenia są preformowane automatycznie. Interpretacja wyników jest nieco trudniejsza, ponieważ musisz wiedzieć, co kryje się za każdą liczbą. Poniżej znajdziesz podział 4 głównych części wyników analizy regresji.
wyjście analizy regresji: podsumowanie wyjście
ta część mówi, jak dobrze obliczone równanie regresji liniowej pasuje do danych źródłowych.
oto, co oznacza każda informacja:
wielokrotność R. Jest to współczynnik korelacji, który mierzy siłę liniowej zależności między dwiema zmiennymi. Współczynnik korelacji może być dowolną wartością z zakresu od -1 do 1, a jego wartość bezwzględna wskazuje na siłę zależności. Im większa wartość bezwzględna, tym silniejsza relacja:
- 1 oznacza silny pozytywny związek
- -1 oznacza silny negatywny związek
- 0 oznacza brak związku w ogóle
R kwadrat. Jest to współczynnik determinacji, który jest używany jako wskaźnik dobroci dopasowania. Pokazuje, ile punktów spada na linię regresji. Wartość R2 jest obliczana z całkowitej sumy kwadratów, dokładniej jest to suma kwadratowych odchyleń oryginalnych danych od średniej.
w naszym przykładzie R2 wynosi 0,91 (zaokrąglone do 2 cyfr), co jest bardzo dobre. Oznacza to, że 91% naszych wartości pasuje do modelu analizy regresji. Innymi słowy, 91% zmiennych zależnych (wartości y) jest wyjaśnione przez zmienne niezależne (wartości x). Ogólnie rzecz biorąc, R kwadrat 95% lub więcej jest uważane za dobre dopasowanie.
skorygowany kwadrat R. Jest to kwadrat r dostosowany do liczby zmiennych niezależnych w modelu. Będziesz chciał użyć tej wartości zamiast kwadratu R do wielokrotnej analizy regresji.
błąd standardowy. Jest to kolejna dobra miara, która pokazuje dokładność analizy regresji – im mniejsza liczba, tym bardziej możesz być pewien swojego równania regresji. Podczas gdy R2 reprezentuje procent wariancji zmiennych zależnych, która jest wyjaśniona przez model, błąd standardowy jest miarą bezwzględną, która pokazuje średnią odległość, że punkty danych spadają z linii regresji.
uwagi. Jest to po prostu liczba obserwacji w modelu.
wyjście analizy regresji: ANOVA
druga część wyjścia jest analiza wariancji (ANOVA):
zasadniczo dzieli sumę kwadratów na poszczególne składniki, które dają informacje o poziomach zmienności w modelu regresji:
- df to liczba stopni swobody związanych ze źródłami wariancji.
- SS jest sumą kwadratów. Im mniejszy pozostały SS w porównaniu z całkowitym SS, tym lepiej model pasuje do danych.
- MS jest kwadratem średnim.
- F jest statystyka F, lub F-test dla hipotezy zerowej. Służy do testowania ogólnego znaczenia modelu.
- Znaczenie F to wartość P F.
część ANOVA jest rzadko używana do prostej analizy regresji liniowej w programie Excel, ale zdecydowanie powinieneś przyjrzeć się temu ostatniemu komponentowi. Znaczenie wartość F daje wyobrażenie o tym, jak wiarygodne (statystycznie istotne) są wyniki. Jeśli Znaczenie F jest mniejsze niż 0,05 (5%), twój model jest OK. Jeśli jest większa niż 0,05, prawdopodobnie lepiej wybrać inną niezależną zmienną.
wyniki analizy regresji: współczynniki
Ta sekcja zawiera szczegółowe informacje o składowych analizy:
najbardziej użytecznym elementem w tej sekcji są współczynniki. Pozwala na zbudowanie równania regresji liniowej w Excelu:
dla naszego zbioru danych, gdzie y to liczba sprzedanych parasoli, a x to średnia miesięczna suma opadów, nasz wzór regresji liniowej wygląda następująco:
Y = Rainfall Coefficient * x + Intercept
wyposażony w wartości a i b zaokrąglone do trzech miejsc po przecinku, zmienia się w:
Y=0.45*x-19.074
na przykład, przy średnich miesięcznych opadach równych 82 mm, sprzedaż parasoli wynosiłaby około 17,8:
0.45*82-19.074=17.8
w podobny sposób możesz dowiedzieć się, ile parasoli będzie sprzedawanych wraz z innymi miesięcznymi opadami (zmienna x), które podasz.
wyniki analizy regresji: pozostałości
jeśli porównasz szacunkową i rzeczywistą liczbę sprzedanych parasoli odpowiadających miesięcznym opadom 82 mm, zobaczysz, że te liczby są nieco inne:
- szacowane: 17.8 (obliczone powyżej)
- rzeczywista: 15 (wiersz 2 danych źródłowych)
dlaczego różnica? Ponieważ zmienne niezależne nigdy nie są doskonałymi predyktorami zmiennych zależnych. A pozostałości mogą pomóc zrozumieć, jak daleko są rzeczywiste wartości od przewidywanych wartości:
jak zrobić wykres regresji liniowej w programie Excel
Jeśli chcesz szybko zwizualizować zależność między dwiema zmiennymi, narysuj wykres regresji liniowej. To bardzo proste! Oto jak:
- wybierz dwie kolumny z danymi, w tym nagłówki.
- na karcie wstawka w grupie Czaty kliknij ikonę wykresu punktowego i wybierz miniaturę punktową (pierwszą):
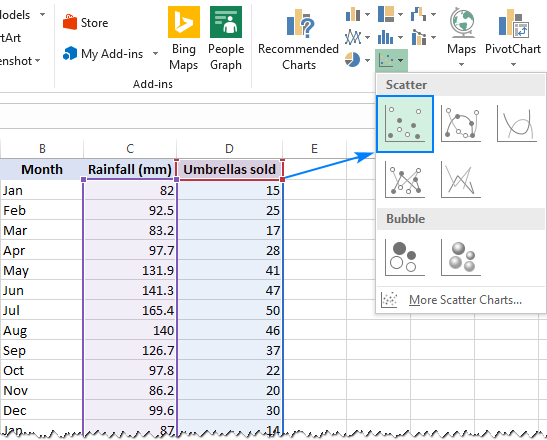
spowoduje to wstawienie wykresu punktowego do arkusza roboczego, który będzie podobny do tego:
- teraz, musimy narysować linię regresji najmniejszych kwadratów. Aby to zrobić, kliknij prawym przyciskiem myszy dowolny punkt i wybierz Dodaj linię trendu… z menu kontekstowego.
- w prawym okienku wybierz liniowy kształt linii trendu i, opcjonalnie, sprawdź wyświetl równanie na wykresie, aby uzyskać wzór regresji:
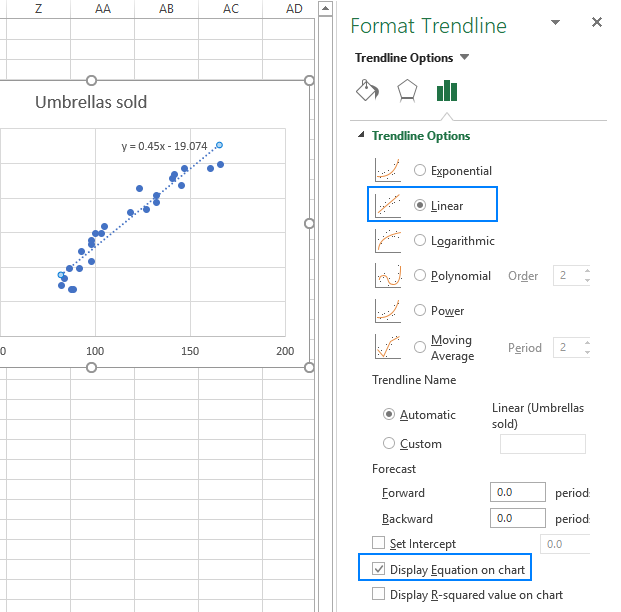
jak możesz zauważyć, równanie regresji stworzone dla nas przez Excela jest takie samo jak formuła regresji liniowej, którą zbudowaliśmy na podstawie współczynników wyjściowych.
- przejdź do zakładki wypełnij & I dostosuj linię do własnych upodobań. Na przykład możesz wybrać inny kolor linii i użyć linii ciągłej zamiast linii przerywanej (wybierz linię ciągłą w polu Typ myślnika):
w tym momencie Twój wykres wygląda już jak przyzwoity Wykres regresji:
mimo to możesz chcieć wprowadzić kilka ulepszeń:
- przeciągnij równanie w dowolne miejsce.
- Dodaj tytuły osi (przycisk elementów wykresu > tytuły osi).
- Jeśli punkty danych zaczynają się na środku osi poziomej i/lub pionowej, jak w tym przykładzie, możesz pozbyć się nadmiernej białej spacji. Poniższa wskazówka wyjaśnia, jak to zrobić: Skaluj osie wykresu, aby zmniejszyć odstęp.
i tak wygląda nasz ulepszony Wykres regresji:
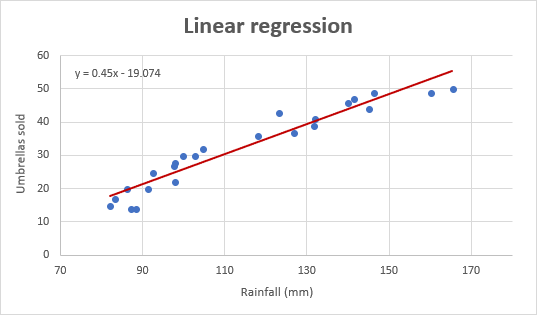Ważna uwaga! Na wykresie regresji zmienna niezależna powinna zawsze znajdować się na osi X, a zmienna zależna na osi Y. Jeśli wykres jest wykreślony w odwrotnej kolejności, zamień kolumny w arkuszu, a następnie narysuj wykres od nowa. Jeśli nie możesz zmienić układu danych źródłowych, możesz przełączać osie X i Y bezpośrednio na wykresie.
jak wykonać regresję w programie Excel za pomocą formuł
Microsoft Excel ma kilka funkcji statystycznych, które mogą pomóc w analizie regresji liniowej, takich jak LINEST, SLOPE, INTERCPET i CORREL.
funkcja liniowa wykorzystuje metodę regresji najmniejszych kwadratów do obliczenia linii prostej, która najlepiej wyjaśnia zależność między zmiennymi i zwraca tablicę opisującą tę linię. Szczegółowe wyjaśnienie składni funkcji znajdziesz w tym samouczku. Na razie stwórzmy formułę dla naszego przykładowego zbioru danych:
=LINEST(C2:C25, B2:B25)
ponieważ funkcja LINEST zwraca tablicę wartości, musisz wprowadzić ją jako formułę tablicy. Wybierz dwie sąsiadujące komórki w tym samym wierszu, E2:F2 w naszym przypadku wpisz formułę i naciśnij Ctrl + Shift + Enter, aby ją zakończyć.
formuła Zwraca współczynnik B (E1) i stałą a (F1) Dla już znanego równania regresji liniowej:
y = bx + a
jeśli unikasz używania formuł tablicowych w Arkuszach, możesz obliczyć A i b indywidualnie za pomocą regularnych formuł:
uzyskaj punkt przecięcia osi y (a):
=INTERCEPT(C2:C25, B2:B25)
uzyskaj punkt przecięcia osi B):
=SLOPE(C2:C25, B2:B25)
dodatkowo można znaleźć współczynnik korelacji (wielokrotność R w podsumowaniu analizy regresji), który wskazuje, jak silnie obie zmienne są ze sobą powiązane:
=CORREL(B2:B25,C2:C25)
poniższy zrzut ekranu pokazuje wszystkie te formuły regresji Excela w działaniu:
tak się robi regresję liniową w Excelu. Należy jednak pamiętać, że Microsoft Excel nie jest programem statystycznym. Jeśli chcesz przeprowadzić analizę regresji na profesjonalnym poziomie, możesz użyć ukierunkowanego oprogramowania, takiego jak XLSTAT, RegressIt itp.
dostępne pliki do pobrania:
aby przyjrzeć się bliżej naszym formułom regresji liniowej i innym technikom omówionym w tym samouczku, zapraszamy do pobrania naszej przykładowej analizy regresji w skoroszycie programu Excel.
- Jak korzystać z Solver w Excelu z przykładami
- Jak obliczyć odsetki złożone w Excelu
- Jak obliczyć CAGR (compound annual growth rate) w Excelu
Leave a Reply